|
|
|
|
|
|
|
|
|
Не хотел Данилов теперь
переводить себя в демоническое состояние еще Что, скажите, привнес компьютер в нашу жизнь нового, неведомого до него? Тексты и раньше набирали на машинках, фотографии ретушировали, музыку проигрывали и сочиняли, верстали газеты и журналы, переписывались, бухгалтеры перелопачивали горы цифр и даже делали сложные детали на станках с ЧПУ. Были разработаны сложные механизмы для прорисовки мудреных кривых, была целая наука о номограммах, умещающих на одном графике несколько функций с разными параметрами. Рискуя навлечь гнев фанатиков бесчисленных вариантов применения компьютеров, заявляю: главное, что он позволил нам увидеть фракталы. Это модное понятие взрывообразно шагает по планете, завораживая своей красотой и таинственностью новые батальоны любителей, и проявляясь в самых неожиданных областях: метеорологии, философии, географии, биологии, механике и даже истории. Есть, например, гипотеза о фрактальной структуре Тунгусского метеорита. Трудно найти журнал, не писавший о фракталах или страничку программиста без галереи фракталов. О необычайной популярности фракталов свидетельствует подмеченный случай – одна знакомая, добрая милая дамочка, проживающая в рамках кухонной плиты, школьных хлопот с детьми и телесериалов, выбирая ткань для платья, сказала: «Красивый рисунок, в нем есть что-то фрактальное». Писать о фракталах вообще – занятие, попадающее под выявленный Козьмой Прутковым закон о невозможности объять необъятное. (Кстати, его вопрос «где начало того конца, которым оканчивается начало?» вполне можно считать предтечей сотен нынешних публикаций о самоподобии фракталов.) Поэтому из множества разделов этой темы мы не будем рассматривать историю фракталов, споры о приоритете Мандельброта в открытии их, не рассмотрим такие фрактальные разделы, как L-деревья (подробнее о них смотрите Жизнь среди ветвей и рекурсий, точечные атракторы (Волшебные точки на экране), снежинку Коха и ковер Серпинского в Компьютерных вестях. Впрочем, тому, кто интересуется математикой, наверняка этот самый ковёр Серпинского хорошо известен. У мэтра популярной математики Мартина Гарднера найдём, что ещё в 1905 году на ежегодной математической олимпиаде в Венгрии предлагалась задача: «Квадрат разделён на 9 частей (как для игры крестики-нолики) и центральный квадрат удалён. Затем каждый из оставшихся 8 квадратов разделён на 9 частей, центральный квадрат удалён и процедура повторяется многократно. Найти предел, к которому стремится площадь полученной фигуры». Так вот – полученная фигура и есть ковёр Серпинского – квадрат настолько дырявый, что он уже ближе к линии. Известны множество объектов, застрявшие на полпути от одного измерения к другому, например, по аналогии с ковром можно представить куб Серпинского, трухлявый как губка, почти не обладающий объёмом. Для таких объектов создано направление математики – теория размерностей, занимающаяся серьёзными приложениями, например, вычисление длины береговой линии из-за изломанности формы не подающееся простым вычислениям. Каждый пустяшный реферат непременно содержит список использованной литературы, причем первыми перечисляются работы авторов, причисленных на данный момент к классикам. Также и приличная статья должна содержать обзор ресурсов Интернета по интересующей нас теме. Если мы зададим слово «фрактал» в любом поисковике, то придем к мысли, что Рунет создавался для фракталов. И, если отбросить анекдоты, знакомства, новости из жизни поп-звезд, пупсики-кроватки и прочие лакомства для буратин с короткими мыслями, то так оно, возможно и есть. Ибо, как каждый юный веб-дизайнер непременно выкладывает «Портфолио» из своих шедевров, так же каждый приличный программист, отдыхая душой от бесконечных корректировок квартального баланса, создает и любовно выкладывает фрактальную галерею. Года четыре назад, когда Рунет был вполне
обозримым и каждый интересный сайт был на виду,
путешествие в мир фракталов начиналось со
странички www.chat.ru/~fractals
содержащей ссылки на фрактальные сайты.
Читателям, доверяющим моему отбору, предлагаю
список самых приятных фрактальных страничек
Рунета, на каждой из которой вы найдете
дальнейшие ссылки на лучшие в понимании их
авторов ресурсы Сети. Помня афоризм о том, что чем шире угол зрения, тем он тупее, ограничимся рассмотрением только лишь комплексных чисел. К сожалению, их (комплексные числа) периодически исключают из школьной программы, а это один из красивейших разделов математики. Комплексное число состоит из реальной (обычного числа) и мнимой части. Мнимая часть содержит квадратный корень из -1, i=(-1)1/2. Разработаны правила действий с комплексными числами, основанные на том, что i в квадрате равно минус 1 (i2= -1). Комплексные числа имеют прикладное значение во многих областях науки, являются основным аппаратом для расчетов в электротехнике и связи. Если на плоскости по горизонтальной оси откладывать реальные числа, а по вертикальной – мнимые, то каждому комплексному числу будет соответствовать точка на этой плоскости. Именно эта возможность «видеть» комплексные числа и действия над ними поразила меня еще в школе, когда о фракталах и речи не было. Например, известно, что корни третьей степени из единицы (один реальный и два комплексных) расположены в вершинах равностороннего треугольника, а корни кубические из –1 тоже лежат на вершинах равностороннего треугольника, но отраженного относительно первоначального вокруг вертикальной оси. А корни седьмой степени из любого числа лежат на вершинах правильного семиугольника. (Кстати вопрос – сможете ли вы нарисовать семиугольную звезду так же, как пятиугольную не отрывая пера от бумаги? А восьмиугольную, а девяти, десяти? А найти общее правило для рисования таких звезд? А программочку…). Каждому комплексному числу соответствует точка на плоскости. Возведем число в квадрат – появляется другая точка, еще раз возведем в квадрат (или любую другую степень), появляется новая точка на плоскости. Потом эту простейшую операцию повторим многократно с получающимся каждый раз новым комплексным числом. В зависимости от начального числа могут быть три варианта: процесс пошел вразнос, число резко растет, уходит «из поля зрения», это не интересно; число быстро уменьшается и исчезает, еще менее интересно; да, да, теперь самое потрясающее. При некоторых начальных значениях новые числа группируются внутри некоторой области, а при отображении их на плоскости появляются невероятные изображения. Это группирование возводимых в квадрат комплексных чисел впервые подметил и описал Жюлиа в 1916 году. И это, так называемое множество Жюлиа, послужило отправной точкой для Бенуа Р. Мандельброта, математика из Исследовательского центра им. Томаса Уотстона при IBM, впервые предложившего термин «фрактал» для описания объектов, структура которых повторяется при переходе к все более мелким масштабам. Так как появляющиеся картинки обладают всеми признаками фракталов. Многие авторы оспаривают первенство Мандельброта, ссылаясь на более ранние работы, но название, тем не менее, закрепилось (как-то же множество надо называть). Подробности выяснения приоритета можно найти в журнале «В мире науки» (Scientific American) №6/1990 г. Однако вернемся к множеству. Суть технологии его получения состоит в следующем. Берется комплексное число. Выбранное число возводится в квадрат и прибавляется какое-то фиксированное постоянное число. Это число тоже комплексное, то есть имеет действительную и мнимую части, подбирая их мы можем регулировать процесс, получая самые причудливые картины. Простейшая итерационная формула Zнов=Z2стар + С, соответствующая множеству Жюлиа, нарисует подобие куклы-неваляшки. Края ее размыты, как бы лохматые. В них то и происходит самое таинство.
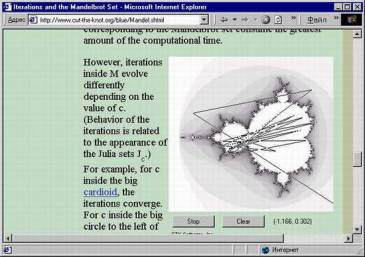
На страничке Cut-The-Knot (разруби узел ) профессора математики Университета Айовы Александра Богомольного, без устали ежемесячно в течение четырех лет публикующего занимательные статьи по всем разделам математики с java-аплетами, находится аплет, удачно иллюстрирующий описанный выше процесс. Если по аплету щелкнуть мышкой, то начинают прорисовываться линии, соединяющие точки, появляющиеся от возведения в квадрат числа, соответствующего точке клика мышки. Если мы щелкаем вне «неваляшки», то наше число после одного-двух возведений в квадрат улетает за рисунок. Причем, чем темнее зона, по которой мы щелкаем, тем больше зигзагов сделает соответствующее число перед «улетом в космос». Если мы щелкнем по белой зоне внутри рисунка, то зигзаг вырождается, сделав пару уменьшающихся ломанных линий. И, самое интересное, если мы щелкнем по «лохматой области», то получим долгое замазывание ломанными линиями зоны рисунка, это мы вызвали к жизни фрактальное множество Мандельброта. Теперь мы готовы к рассмотрению практической реализации рассмотренного процесса, но прежде два лирических отступления. Средняя женщина предпочитает быть красивой, а не умной, потому что средний мужчина лучше видит, чем соображает Отступление первое. Почему же фракталы так красивы? Так сказочно, обворожительно, волнующе (какие еще есть эпитеты?) красивы. Так красивы, что материалисты-циники, с усмешкой отбрасывающие многочисленные брошюры, выводящие наличие Бога из красоты окружающего мира, просто в недоумении. «Когда передо мной прекрасный часовой механизм, я невольно думаю об авторе, сотворившем его» – восклицал Бенедикт Спиноза. Размышления и восторги по поводу красоты фракталов, может, и не приведут нас в Церковь (наверное, этого недостаточно), но оставят в изумлении. Ведь если красота горных вершин, звездного неба или морского прибоя ожидаема, привычна (а как же иначе?), то откуда же берется красота возводимых в квадрат комплексных чисел? Математика вся пронизана красотой и гармонией, но одно дело математика предметная, имеющая дело с реальными вычислениями и измерениями, и совсем другое дело комплексные числа. Ведь они выдуманы человеком, искусственно назначившим правила их существования и действия над ними. В этом отношении они сродни шахматам – искусственно придуманным правилам жизни некоторых объектов. И тоже несущих в себе красоту, (помимо спортивного азарта). Как-то, разбирая партии Капабланки, я был поражен, сколько в них интриги, остроумия и изящества. (К сожалению, позже, особенно с приходом Петросяна, красота партий шахматистов верхних эшелонов стала менее доступной для простых любителей, постоянные неочевидные попытки улучшения труднопонятных позиций, но, скорее всего, я просто слаб в шахматах.) Отступление второе. Фракталы связаны кроме всего прочего и с биологией. При определенных условиях хаос (так называемый…) возможно может стихийно, или по неизвестным пока законам, создавать некоторые самоорганизующиеся структуры. Если эта гипотеза подтвердится, то мы получим ответ на вопрос о происхождении жизни, а важнее его вряд ли вообще есть вопросы. Подключайтесь – вряд ли вы найдете более достойное применение отпущенной вам способности мыслить. Заинтересовавшиеся могут найти в Сети
интересные статьи по синергетике и теории Хаоса.
Нас же более интересует то, что некоторые
фрактальные рисунки похожи на клеточные
организмы. Это дает простор для фантазии – можно
изучать законы жизни вами же созданных так
называемых биоморфов, с удивлением открывая у
своих детищ черты, присущие настоящим
организмам. Например, почитайте«Изучение
законов наследственности у биоморфов» .
– Спасибо, Пятачок, - сказал Иа. Итак, мы рассматриваем в цикле (точнее, в двух циклах, по x и по y) точки плоскости в выбранном диапазоне. Каждую точку превращаем в комплексное число, получая действительную составляющую (RE) из координаты по х и мнимую составляющую (IM) из координаты по y с помощью масштабного коэффициента. Для возведения комплексного числа в квадрат применим подпрограмму QWA. Поясним, как получились ее формулы. Запишем комплексное число в виде z=a+bi, где a и b его дейстительная и мнимая составляющие. Найдем квадрат этого числа: z2=(a+bi)*(a+bi)=a2+abi+abi+(bi)2=a2+2abi-b2=(a2-b2)+2abi или в наших символах re1=re*re-im*im – действительная часть после возведения в квадрат im1=2*re*im – мнимая часть после возведения в квадрат. Теперь открываем цикл (со счетчиком v), в теле которого возводим число в квадрат, вызывая QWA, потом добавляем фиксированное число к каждой составляющей комплексного числа, потом проводим анализ для выхода из цикла, например, по достижению переменными re и im какого либо значения. Значение счетчика цикла v запоминается и именно оно служит для определения цвета в данной точке. В этом и состоит изюминка алгоритма получения красивого изображения – разные точки выходят при разных значениях счетчика и группируются по цветам в замысловатые узоры. После выхода из цикла еще вводим условия для рисования цветом v, а остальные области заполняем черным цветом. Теперь, подбирая масштаб, фиксированное число (точнее две его составляющие), условие выхода и условия рисования получим картинку, соответствующую приведенному листингу программы.
Попробуйте поменять параметры и вы увидите, как фиксированное число влияет на вид сердцевины рисунка, условия выхода и условия рисования на заполненность его цветом и на длину колючек, причем ограничения по re и по im влияют каждый на свои колючки, поиграйте с программой – невозможно оторваться от этих экспериментов. А мы делаем следующий шаг – задаемся вопросом, а почему бы не попробовать возводить число в куб? Никаких ограничений нет, и мы создаем подпрограмму KUB. Помня шутку о том, что каждая добавленная в книгу формула вдвое сокращает число ее покупателей, выводить формулу куба комплексного числа не будем, вы это запросто проделаете сами, помня, что i2=-1. А вот и текст подпрограммы:
И картинка от запуска той же программы с единственной заменой QWA на KUB из которой видно, что внутри нашего фрактала плавают теперь не два, а три организма, внутри которых тоже не по два, по три более мелких. Дальше вы уже знаете, что можно сделать – задать два раза подряд QWA ; QWA для возведения в четвертую степень и получить организм с четырьмя штучками внутри. Задав QWA; KUB; получим шестую степень, а KUB; KUB; - соответственно, девятую степень комплексного числа. Варианты сочетаний степеней с подобранными к ним фиксированным числом и условиями выхода бесконечны. Приведу лишь два самых интересных. На первом из них мы видим сказочное окно в волшебный мир,
вот фрагмент программы для его получения.
А на втором, самом, можно сказать, фрактальном, мы видим страшную сказку из бесконечной вложенности самоподобных элементов. Сначала при мелком масштабе мы видим мрачную черную колючку, внутри которой плавают три голубых организма, тоже с черными колючками, одна из которых, самая страшная, больше других.
Увеличиваем масштаб, опускаясь внутрь чудища, и видим, что в каждом из трех голубых организмов расположились по три красных с черными колючками, одна из которых…, в каждом красном живут по три розовых, в них по три желтых, в них по три белых… и все с черными колючками.
И вот фрагмент кода для этих фантастических существ фрактального микромира. Какой следующий ход в нашем движении по созданию картинок из жизни комплексных чисел? Конечно же переход к полноценному 24-битному представлению цвета, которое позволяют получить языки программирования в среде Windows. Например, Visual Basic, в который мы перенесем отлаженный в Турбо Паскале алгоритм. Даже используя только возведение чисел в квадрат за счет подбора масштаба, фиксированного числа, условия выхода и коэффициентов для каждой составляющей цвета можно получать невероятно красивые картины. Именно ими на 99% заполнены бесконечные фрактальные галереи в Сети. Приводим листинг исполнения и один из бесчисленных вариантов подобранных параметров с полученной картинкой.
Видно, что алгоритм точно такой же, что и в Паскале, только возведение в квадрат не вынесено в подпрограмму. Попробуйте поменять коэффициенты, на которые умножается счетчик цикла для получения разных цветов при выводе точки и вы увидите, как сильно поменяется вид рисунка. Что дальше? Казалось бы, что уже нарисовали все стороны жизни комплексных чисел. Но это не так, есть еще один шаг, открывающий новые возможности для красивых опытов, а именно – применение формулы Муавра для возведения в степень комплексных чисел. Каждое комплексное число вида z=a+bi можно представить в виде z=r*cos(fi)+r*sin(fi), где r=(a2+b2)1/2 – так называемый модуль комплексного числа, а fi=atn(a/b) – угол между отрезком, соединяющим начало координат с нашим числом и осью действительных чисел. Использование формулы Муавра позволяет возводить комплексное число по очень изящному соотношению: zn=rn*cos(n*fi)+rn*sin(n*fi) А самое интересное, что используя эту формулу мы можем возводить комплексное число не только в натуральную, но и в дробную и отрицательную степень. Вообще говоря можно возводить даже и в комплексную степень, но это уже совсем выходит за рамки забав с картинками. Вот пример реализации – картинка, полученная возведением числа в девятую степень с применением формулы Муавра и листинг программы.
Небольшие тонкости, в которых, впрочем, читатели наверняка разберутся сами: при вычислении угла через арктангенс надо обойти деление на нуль и учесть, что область определения арктангенса первая и четвертая четверть, поэтому для отрицательных значений re к полученному углу добавляется пи. На этом же Арбузе расположен Java-аплет, рисующий фракталы по формуле Муавра, причем масштаб, сдвиги фиксированным числом реальные и мнимые, условие выхода и коэффициенты для каждого цвета можно задавать на свой вкус, любуясь полученными чудесами. Забавляясь с аплетом или с самодельными программами вы заметите, что у появляющихся организмов число отростков или голов равно показателю степени для целых значений степени.
Для дробных узор рассыпается, появляются разрывы на контуре, зато при отрицательных значениях показателя степени появляются цветы и фантастические бабочки невиданной красоты. Если вы захотите воспользоваться готовой программой для исследования или просто рисования фракталов, то главная рекомендация моя (и многих других “фрактальных” авторов) это Fractal Explorer киевлян А. Сиротинского и О. Федоренко. Я знаком с разными ее версиями уже несколько лет, невероятно много настроек, выбор вида фрактала, его параметров, в общем, то, что надо. Еще снова порекомендую «речку», о которой говорили выше и программу моего знакомого по переписке Андрея, расположенную здесь.. На этом и закончим, успеха вам в экспериментах с таинственной красотой фракталов. |
| Автор | )c( 2000-2019 Kопирайта нет, копируйте на здоровье :) 100112 лет в Интернете |
|