Жизнь среди ветвей и рекурсий

Несчастный мистер Бэггинс был не большой мастак лазать по деревьям,
но делать нечего – его посадили на нижние ветки исполинского дуба,
росшего на обочине, и хочешь не хочешь, а пришлось карабкаться вверх.
Бильбо продирался сквозь густые сучья, ветки хлопали его по лицу, кололи глаза.
Дж. Р. Р, Толкиен. Хоббит, или туда и обратно.

Если ученые продолжают настаивать на нашем происхождении от мартышек, то имеет право на озвучивание и авторская гипотеза: «Наблюдение веток на деревьях во время лазания по ним и размышление об их количестве, толщине, направленности и фрактальном рисунке дало толчок развитию разума». И стимулировало его развитие на следующих этапах. И процесс этот продолжается, в том числе и при чтении нижеследующего.

Ветка первая. Великий Леонардо и волны на бирже.

Представьте – ствол дерева пускает новую ветвь, на следующий год он «отдыхает» и только через год пускает еще одну ветвь – точно так же ведет себя каждая ветвь. Поэтому сначала имеется только главный ствол, на следующий год – две ветви, еще год спустя – три, потом 5, 8, 13. Полученная последовательность чисел известна как ряд Фибоначчи и занимает важное место в математике, так как проявляется в самых неожиданных ее приложениях. Строгое определение этого ряда чисел звучит так: каждое число ряда, начиная со второго, равно сумме двух предыдущих.   Леонардо Фибоначчи из Пизы первым познакомил европейцев с арабскими цифрами и десятичной системой, которые он узнал от арабов, обучаясь в Алжире. До него использовали неуклюжую и громоздкую римскую систему, тормозящую развитие и использование математики. Подробнее о Фибоначчи и приложениях его работ смотрите на http://www-groups.dcs.st-and.ac.uk/~history/Mathematicians/Fibonacci.html и на http://www.mcs.surrey.ac.uk/Personal/R.Knott/Fibonacci/fibBio.html Заслуги Леонардо оценены итальянцами – они ему поставили памятник недалеко от знаменитой Падающей башни. Но самым главным памятником средневековому математику служит названная его именем числовая последовательность. В последнее время числа Фибоначчи известны не только любителям математики, но и бизнесменам, экономистам, и игрокам на бирже. Замечено, что волны Эллиота, описывающие колебания котировок ценных бумаг, являются огибающими маленьких волн, те, в свою очередь, еще более мелких, а количество мелких колебаний в периоде более крупного соответствует ряду Фибоначчи. Если вы разберетесь с числами Фибоначчи и волнами Эллиота, то можете разбогатеть, играя на бирже ценных бумаг. Заинтересовавшиеся могут зайти на сайт компании Elliott Wave International в интернете http://www.elliottwave.com . Если плохо с английским, а разбогатеть хочется - то заходите на http://user.cityline.ru/~esfinkro/index.htm , там есть доступно изложенная статья о Волнах Эллиота.

По иронии судьбы Леонардо, внесший существенный вклад в развитие математики, в наши дни известен потому, что живший в позапрошлом веке французский математик Эдуард Люка назвал именем Фибоначчи числовую последовательность, возникающую в одной довольно тривиальной задаче из «Книги об абаке», написанной Леонардо в 1202 году. Вот эта задача в том виде, как формулирует ее сам Фибоначчи.

«Пара кроликов через месяц производит на свет другую пару, а потомство они дают со второго месяца после своего рождения. Итак, через месяц будет две пары, через два месяца – три пары, а через четыре месяца – пять, так как к паре, рожденной первой парой добавятся первые дети от второй пары…». Продолжая процесс (конечно, лучше карандашом на бумаге), мы и получим количество пар кроликов по месяцам: 1, 1, 2, 3, 5, 8, 13, 21, 35, 56… – эти числа и представляют ряд, названный по имени автора задачи.

С начала ХIХ века работы, посвященные числам Фибоначчи, начали, как выразился один математик, «размножаться как фибоначчиевы кролики». Эти числа привлекли математиков своей особенностью возникать в самых неожиданных местах. Замечено, например, что отношения чисел Фибоначчи, взятых через одно, измеряют угол между соседними листьями на стебле растений, точнее говоря, какую долю оборота составляет этот угол: 1/2 – для вяза и липы, 1/3 – для бука, 2/5 – для дуба и яблони, 3/8 – для тополя и розы, 5/13 – для ивы и миндаля и т.д. Также, эти числа вы найдете при подсчете семян в спиралях подсолнуха, в количестве лучей, отражающихся от двух зеркал, в количестве вариантов маршрутов переползания пчелы от одной соты к другой, во многих математических играх и фокусах.

Наиболее замечательное свойство ряда Фибоначчи состоит в том, что отношение двух последовательных членов ряда попеременно, то больше, то меньше отношения золотого сечения и с возрастанием номера члена ряда разность между его отношением к предыдущему члену ряда и отношением золотого сечения стремится к нулю. О золотом сечении мы еще как-нибудь поговорим поподробнее.

Еще несколько интересных свойств чисел Фибоначчи.

Квадрат любого числа F_n на единицу отличается от произведения F_n-1* F_n+1. Знак разности F_n²  - F_n-1 * F_n+1  при переходе от n к n+1 изменяется на противоположный.

Для любых четырёх последовательных членов ряда Фибоначчи A, B, C и D справедливо соотношение C²–B²=A*D.

Последние цифры чисел Фибоначчи образуют периодическую последовательность с периодом 60. Если от каждого числа брать по две последние цифры, то они также образуют последовательность с периодом, равным 300.

Каждое третье число Фибоначчи делится на 2, каждое четвертое – на 3, каждое пятое – на 5, каждое шестое – на 8 и т.д., делители сами образуют ряд Фибоначчи.

Если не считать F₄=3, то всякое число Фибоначчи, которое простое, имеет простой индекс (например, число 253 простое, и индекс его, равный 13, также прост) К сожалению, обратное утверждение справедливо не всегда: простой индекс отнюдь не означает, что соответствующее число Фибоначчи простое. Первым примером служит F₁₉=4181. Индекс его прост, но само число разлагается на множители: 4181=37*113.

Единственным квадратом среди чисел Фибоначчи является F₁₂=144, причем его значение совпадает с квадратом индекса.

Прервемся на этом, желающие подробнее познакомиться с числами Фибоначчи найдут еще много интересного в книгах по занимательной математике Мартина Гарднера, Гуго Штейнгауза и других популяризаторов науки. Мы же рассмотрим эти числа как идеальный “полигон” для знакомства с рекурсией.

Ветка вторая. Космическая частица и рекурсия.

Сначала поясним, что такое рекурсия. Во всех языках программирования можно описать функцию, как подпрограмму с параметром, и вызывать ее при необходимости. Если же функция в процессе выполнения вызывает сама себя, то такой прием называется рекурсией.

Тут мы предлагаем читателям задуматься – что значит, функция вызывает сама себя? Обычно конструкции языков программирования можно более или менее представить и проиллюстрировать примерами из реальной жизни. Если условие выполняется – делай то-то, иначе – что-то другое. Ясно. Выполняй, пока условие выполняется – ясно. Цикл со счетчиком For-next одна знакомая, преподающая программирование, иллюстрировала известной зацикленной песенкой:

«Полсотни негритят пошли купаться в море
Полсотни негритят резвились на просторе
Один из них утоп, ему купили гроб
И вот вам результат – сорок девять негритят…»

А как же представить наглядно функцию, вызывающую самою себя? Лучшей моделью, на наш взгляд, служит английский стишок «Дом, который построил Джек», а еще лучшей – пародия на него, стишок команды КВН Физтеха из книжки «КВН раскрывает секреты» вышедшей аж в 1967 году (М. Молодая гвардия)

Вот стенд, который построил студент,
А вот космическая частица,
Которая с бешеной скоростью мчится
В стенде, который построил студент.
А вот инженер молодой, бледнолицый,
Который клянет и судьбу и частицу,
Которая с бешеной скоростью мчится
В стенде, который построил студент.
А вот кандидат, горделивый не в меру,
Который блистательно сделал карьеру,
Совместно работая с тем инженером,
Который клянет и судьбу и частицу,
Которая с бешеной скоростью мчится
В стенде, который построил студент.
А вот начальник, на вид простоватый,
Который был шефом того кандидата,
Который блистательно сделал карьеру,
Совместно работая с тем инженером,
Который клянет и судьбу и частицу,
Которая с бешеной скоростью мчится
В стенде, который построил студент.
А вот консультант от академии,
С которым встречался время от времени
Тот самый начальник, на вид простоватый,
Который был шефом того кандидата,
Который блистательно сделал карьеру,
Совместно работая с тем инженером,
Который клянет и судьбу и частицу,
Которая с бешеной скоростью мчится
В стенде, который построил студент.
А вот отчетов горы бумажные,
В которых копалась комиссия важная,
Которая выдала крупную премию,
Тому консультанту из академии,
Начальнику дали за вид простоватый,
Кусок уделили тому кандидату,
Который блистательно сделал карьеру,
Остатки вручили тому инженеру,
Который уже не ругает частицу,
Которая с бешеной скоростью мчится
В стенде, который построил
СТУДЕНТ

Теперь, надеемся, всем ясно, что такое рекурсия, позволяющая писать компактные программы. (Представьте, как сократиться стишок, если вместо повторов строк вызывать предыдущие строки с последующим углублением каждый раз.) Компактные с точки зрения кодирования программы, но не с точки зрения быстродействия. Приводим текст программы в среде Turbo Pascal'a, выводящей на экран номер и значение числа Фибоначчи, вычисляемого в функции Fib. Причем, сама функция Fib, кроме оговоренных первого и второго чисел, обращается сама к себе, чтобы сложить два предыдущих значения ряда.

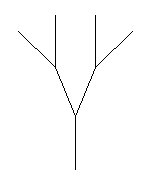
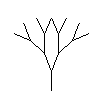
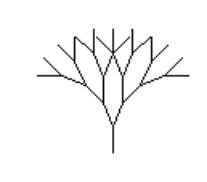
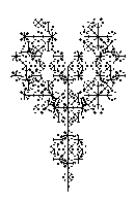
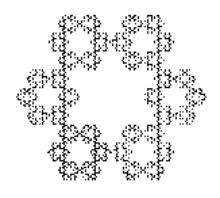
program m; {Программа расчета чисел Фибоначчи}
uses crt;
VAR I : INTEGER ; C: CHAR ;
FUNCTION FIB (T:INTEGER): LONGINT ;
begin
IF (T=1) OR (T=2) THEN Fib:=1 ELSE Fib:=FIB(T-1)+FIB(T-2) end;
BEGIN
CLRSCR ;
FOR I:=1 TO 10 DO BEGIN
       WRITELN(I,' ',FIB(I),' ',I+10,' ',FIB(I+10)) ;
END;
C:=READKEY ;
END.

Результат работы программы:

1   1    11 89
2   1    12 144
3   2    13 233
4   3    14 377
5   5    15 610
6   8    16 987
7  13    17 1597
8  21    18 2584
9  34    19 4181
10 55    20 6765

Проследим, например, как работает рекурсивная функция при вычислении пятого члена ряда Фибоначчи. Для пятого члена значение функции должно равняться сумме четвертого и третьего членов. При вычислении четвертого члена функция обратиться к третьему и второму, при вычислении третьего – ко второму и первому, которые равны единице. Подобное «погружение» произойдет и при вычислении третьего члена как слагаемого четвертого. То есть мы видим, что в данном случае применение рекурсии на редкость неэффективно, мы заставляем процессор совершать множество «движений», причем их количество лавинообразно растет с ростом номера числа в ряду. Если первые десять чисел появляются на экране моментально, следующие с видимой и растущей задержкой, двадцатое на Pentium’e III (700МГц, 64МБ ОЗУ) «пережевывалось» около 5 секунд. (Сороковое – около минуты.) И вся красота и изящность компактного написания программы свелась на нет, даже пошла во вред производительности. Зато, мы теперь знаем, что такое рекурсия, и применим ее где-нибудь с меньшими потерями для пользователей. Обратите внимание на тип функции Longint – длинное целое, если дать тип Integer, то числа, большие 32000 будут представлены неверно. Хотелось бы обратить внимание читателей на связку – во всех книгах по программированию рекурсия иллюстрируется именно вычислением членов ряда Фибоначчи, и, часто, наоборот, при рассказе о числах Фибоначчи вспоминается рекурсия. А как же надо было составлять программу для эффективной работы? Задать массив и заполнять его такой же функцией, но без рекурсии, обращаясь к уже посчитанным членам ряда, помещенным в массив. Программа будет работать «мгновенно», но все это будет уже не так красиво и не так интересно. Как говорит Жванецкий, главное процесс, а результат никого не интересует. Ну вот, пока и всё. Уверены, что вы обязательно когда-нибудь столкнетесь с процессом, в котором узнаете знакомые теперь числа Фибоначчи.

Ветка третья. L-системы L-деревьев.

Любителям фракталов и математических картинок известны фантастические изображения растений, полученные с помощью программ. Это так называемые L-системы. В основе их построения лежат два принципа. Первый – это так называемая «черепашья графика» (оператор draw) патриарха GWBASIC и его детей Turbo Basic и QBasic, когда движение рисуется пошагово в приращениях относительно текущей точки. В более «солидных» языках этого оператора нет, но его легко смоделировать, задавая движение в приращениях координат. Второй принцип – изюминка метода: каждое единичное движение заменяется на весь рисунок. Например, нарисуем вилку-рогатульку. На следующем шаге работы программы каждая из трех палочек вилки заменяется такой-же вилкой, превращая вилку в ветку с сучками, после следующего шага получим лохматый куст, потом пушистое дерево, красивое, фрактальное. Меняя вид начальной картинки можно получать самые разные изображения от зонтиков укропа до колючего перекати-поле или пучка водорослей. Лучшей отправной точкой для путешествия в мир L-систем является страничка Fantastic Fractals   На ней можно найти алгоритмы построения деревьев разных видов с иллюстрациями.

Рассмотрим, как кодируются >L>-системы в общепринятых обозначениях.
Движение вперед обозначается буквой F (Forward – вперед), поворот по часовой стрелке обозначим «+», а против – «-», причем само значение поворота задается в программе и постоянно для всех движений. Буквой В (Back– назад) обозначается возврат без прорисовки, нам это не пригодится.
Для нас важнее механизм возврата. Точка, в которую надо возвращаться, обозначим «[», а место, откуда происходит возврат, обозначим «]». Тогда вилка будет иметь вид: F – движение вперед [ – запомнить позицию + – поворот вправо на 22.5 (например) градусов F – движение вперед после поворота ] – возврат в запомненную позицию [ – запомнить позицию - – поворот влево относительно направления в запомненной точке F – движение вперед после поворота ] – возврат в запомненную позицию
Это движение можно закодировать. Можно и более сложное. Можно закодировать и следующий шаг – замену каждого прямого отрезка на такую же вилку. Два шага нарисуют, три шага - четыре шага Это движение можно закодировать. Можно и более сложное. Можно закодировать и следующий шаг - замену каждого прямого отрезка на такую же вилку. Два шага нарисуют, три шага - четыре шага Прорисовывать каждый шаг заменой текста программы довольно утомительно, и мы вспоминаем о рекурсии. Самое подходящее для нее место! Выполнив необходимые хлопоты с унификацией переменных и передаче значений координат точек возврата, мы добиваемся, что любое дерево рисуется по заранее заданной формуле одной маленькой процедуркой, которая сама себя и вызывает. Приводим текст программы на Visual Basic’e. Предварительно надо открыть форму и разместить на ней таймер. Это позволит с восхищением (ибо порядок прорисовки фрактально-непредсказуем) отслеживать на экране рост дерева. (Отступы пропали при переносе в html, но если вы скопируете в VB6 - все будет работать)

Option Explicit
Dim F(50) As String
Dim X(10) As Single
Dim Y(10) As Single
Dim Fi(10) As Single
Dim Xtemp(10) As Single
Dim Ytemp(10) As Single
Dim Fitemp(10) As Single
Dim Xtemp2(10) As Single
Dim Ytemp2(10) As Single
Dim Fitemp2(10) As Single
Dim k As Integer
Dim Kmax As Integer
Dim vetka As Integer
Dim i(10) As Integer
Dim Xnew As Single
Dim Ynew As Single
Private Sub Form_Load()
k = 1
Kmax = 4
vetka = 300 / Kmax ^ 2.5
X(0) = 700
Y(0) = 500
Fi(0) = 0
F(1) = "-"
F(2) = "f"
F(3) = "+"
F(4) = "f"
F(5) = "+"
F(6) = "["
F(7) = "+"
F(8) = "f"
F(9) = "-"
F(10) = "f"
F(11) = "-"
F(12) = "]"
F(13) = "-"
F(14) = "["
F(15) = "-"
F(16) = "f"
F(17) = "+"
F(18) = "f"
F(19) = "+"
F(20) = "f"
F(21) = "]"
End Sub
Sub Cicl()
X(k) = X(k - 1)
Y(k) = Y(k - 1)
Fi(k) = Fi(k - 1)
DoEvents
For i(k) = 1 To 50
If F(i(k)) = "-" Then
Fi(k) = Fi(k) - 3.14 / 8
If F(i(k)) = "f" Then
If k = Kmax Then Drw X(k) = Xnew: Y(k) = Ynew
Else k = k + 1
Cicl k = k - 1
X(k) = X(k + 1)
Y(k) = Y(k + 1)
End If
End If
If F(i(k)) = "+"
Then Fi(k) = Fi(k) + 3.14 / 8
If F(i(k)) = "[" Then
Xtemp(k) = X(k): Ytemp(k) = Y(k): Fitemp(k) = Fi(k)
If F(i(k)) = "]" Then
X(k) = Xtemp(k): Y(k) = Ytemp(k): Fi(k) = Fitemp(k)
If F(i(k)) = "[[" Then Xtemp2(k) = X(k): Ytemp2(k) = Y(k): Fitemp2(k) = Fi(k)
If F(i(k)) = "]]" Then X(k) = Xtemp2(k): Y(k) = Ytemp2(k): Fi(k) = Fitemp2(k)
Next i(k)
End Sub
Sub Drw()
Xnew = X(k) + vetka * Sin(Fi(k))
Ynew = Y(k) - vetka * Cos(Fi(k))
Line (X(k), Y(k))-(Xnew, Ynew), RGB(0, 55, 0)
End Sub
Private Sub Часы1_Timer()
Cicl
Часы1.Enabled = False
End Sub

Именно эта программа нарисует ветку, клонимую ветром. Меняя переменную Kmax можно уменьшать или увеличивать глубину рекурсии, или, что тоже самое, «пушистость» ветки. А меняя закон движения можно получать самые удивительные и фантастические изображения.

 

Ветка четвертая. Речка.

Желающих получить больше информации об этих удивительных деревьях приглашаем посетить лучшую в Рунете Речку, протекающую по самым приятным областям занимательного программирования - фракталам, паутине и, конечно, L-деревьям. Там вы найдете алгоритм построения объемного дерева с возможностью просмотра его стереоизображения и рассуждения о толщине веток. С ссылкой на самого Леонардо да Винчи Речка предполагает, что суммарная площадь сечения всех веток и ствола на любой высоте постоянна, поэтому видимая ширина ствола и веток уменьшается пропорционально квадратному корню из числа веток. Не правда ли красивая идея? Можно воплотить ее при рисовании L-деревьев для достоверности картины, как это сделали авторы Речки. Можно попытаться раскрасить деревья, задав, например, красный цвет, зависящим от счетчика цикла i(k) и получить куст, у которого все левые сучки красного цвета. Но, все-таки, деревья красивы именно фрактальными узорами, фантастически похожими на настоящие растения.

Ветка пятая, последняя. Задание на дом тем, кто дочитал до конца.

1.Сходите в Ботанический Сад и на разных деревьях проверьте, совпадает ли увеличение количества веток с рядом Фибоначчи. Если лень ехать, можно воспользоваться веточками цветной капусты.
2. Я сообщаю сплетню каждые два часа новому собеседнику, каждый из которых, подумав один час, распространяет ее таким же образом. Как будет расти количество «просвещенных» по часам?
3. Попробуйте вывести общую формулу для чисел Фибоначчи, вычисляющую число по его порядковому номеру в ряду.
4. А если начать не с единицы, а с другого числа, какие свойства будут у этого ряда?
5. Как посчитать фрактальную размерность L-деревьев?
6. Если вместо палочек нарисовать контур человечка и заставить его расти по принципу L-систем, то полученную модель можно использовать в медицине, в проектировании одежды или где-нибудь еще. Как бы вы назвали эту модель?

В соавторстве с Максимом Меметовым