Две фрактальных задачки

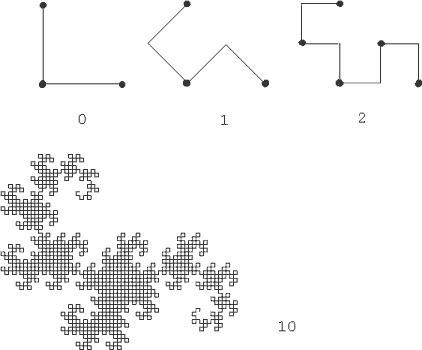
Драконова ломаная

Драконова ломаная - это очень стильный геометрический объект. Его татуированное изображение запросто могло бы украсить тело какого-либо прославленного бойца кунг-фу. Глядя на драконову ломаную, сразу вспоминается Шаолиньский монастырь, а в ушах звучит загадочная пентатоническая музыка.

Драконова ломаная относится к классу самоподобных рекурсивно порождаемых геометрических структур. Ломаная нулевого порядка представляет собой просто прямой угол. Изображение фигуры каждого следующего порядка строится путем рекурсивных замен каждого из отрезков фигуры младшего порядка на два отрезка, сложенных также в виде прямого угла.

При этом каждый первый угол оказывается "вывернутым" наружу, а каждый второй - вовнутрь.

Несмотря на внешнюю простоту, построение драконовой ломаной - увлекательная алгоритмическая задачка, решение которой может потребовать от вас определенных мыслительных усилий. Попробуйте "научить" ваш компьютер строить драконовы ломаные n - того порядка (естественно, в разумных пределах значений n). Это умственное упражнение будет способствовать оттачиванию вашего "боевого" искусства алгоритмизации и программирования. На рисунке проиллюстрирован алгоритм построения драконовой ломаной и изображен вполне взрослый "дракон" десятого порядка.

Треугольник Сьерпинского

Обычный треугольник - это вполне конкретная, "осязаемая" геометрическая фигура. Нет ничего проще, чем представить себе треугольник сделанным из стекла или жести. Мысленно вырежем из него кусок треугольной формы, который своими вершинами будет упираться в середины сторон исходного треугольника. Теперь он будет состоять из трех треугольников и треугольной дырки в середине. Повторим ту же самую операцию с тремя вновь образовавшимися треугольничками. После этого исходный треугольник уже будет состоять из девяти еще меньших треугольников и четырех треугольных пустот. Если мы будем повторять операцию вырезания вновь и вновь, то в конце пути, после бесконечного количества вырезаний, получим искомую фигуру - треугольник Сьерпинского.

Если исходный треугольник был монолитен, то теперь его "тело" стало почти бесплотным. Нельзя быть до конца уверенным, наткнется ли на преграду точка, вдруг вздумавшая пролететь сквозь треугольник Сьерпинского. Что же останется от сплошной исходной фигуры в результате серии бесконечных вырезаний? Попробуйте изобразить это на своем компьютере.

А. КОЛЕСНИКОВ,
andr61@mail.ru

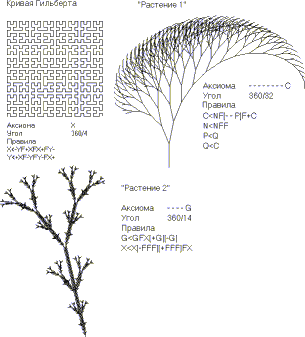
L-фракталы

Ниже мы рассмотрим достаточно общий алгоритм, позволяющий строить множество самоподобных фрактальных структур, в том числе очень напоминающих объекты живой природы. Не так давно по телевизору транслировался научно-популярный фильм BBC о глубоководной жизни, который буквально заворожил меня. Потрясающе красивые съемки, сделанные с глубоководных аппаратов, действовали почти гипнотически, приковывая взгляд к экрану. Животные, обитающие на глубинах в несколько километров в царстве вечной темноты и огромного давления, имеют, как правило, хрупкие, абсолютно прозрачные тела, тут и там обрамленные разноцветным фосфоресцирующим свечением. Их изысканные формы практически полностью основаны на принципах, которые будут обсуждаться ниже.

Задумывались ли вы когда-нибудь, откуда в вашей голове рождаются новые оригинальные идеи (если, конечно, таковые хотя бы иногда вас посещают). Они рождаются как бы спонтанно из хаоса подсознательного. По выражению новосибирского философа А.Г.Чусовитина, "Разум - это бухгалтер мысли, но не ее творец"^*. Однако эти внезапные озарения не происходят сами собой, беспричинно. Как правило, стимулом или катализатором творческого процесса выступают иные оригинальные мысли, приходящие извне. К числу таких "взрывных" эвристичных идей, думается, с полным правом можно отнести принцип L-формализма, предложенный биологом Аристидом Линдермауером для кодирования квазифрактальных самоподобных геометрических структур (см. онлайновый номер журнала "Информатика", расположенный по указанному ниже адресу).

Суть L-кодирования сводится к следующему. Представим себе некое виртуальное программируемое устройство, состоящее из пера, управляющего им механизма и листа бумаги. Управляющий пером механизм способен исполнять несколько команд. А именно: он может опустить перо на бумагу и вычертить прямой отрезок заданной длины в направлении текущей ориентации пера (команда F). Он может изменить ориентацию пера по отношению к текущей на какой-то заданный относительный угол по часовой или против часовой стрелки (команды + и -). Он может также запоминать (заносить в стек) свое текущее состояние (команда [) и вспоминать (извлекать из стека) ранее запомненное состояние (команда ]). Под состоянием в данном случае понимается тройка чисел (x, y, a), где x и y - это координаты пера и а - это угол, определяющий направление ориентации пера. Таким образом, задав некое начальное направление а0, определив относительный угол поворота в 900 и задав длину отрезка, при помощи последовательности команд F+F+ F+F мы можем нарисовать квадрат. Определив относительный угол поворота в 600, при помощи последовательности команд F++F++F можно нарисовать равносторонний треугольник.

Предположим также, что в программы для нашего виртуального устройства, кроме пяти перечисленных команд, можно включать любые другие символы, которые управляющий механизм будет просто игнорировать. То есть если мы введем программу F+BF+CCF+CF, то устройство все равно нарисует квадрат. Теперь мысленно оснастим наше устройство приставкой, которая перед тем, как передать введенную программу на управляющий механизм, может заданное число раз просматривать ее, и при каждом очередном просмотре заменять любые символы последовательности по предварительно указанным правилам. Исходную программную последовательность символов теперь будем называть аксиомой. Например, введем аксиому FB+, и определим правило B < F+FB. Зададим также количество просмотров, равное, например, двум. Тогда на входе механизма после обработки введенной аксиомы приставкой получим последовательность FF+FF+FB+. Вот, собственно, и все. При помощи описанного несложного виртуального устройства можно строить множество самых разнообразных фрактальных форм - от традиционных математических фракталов, таких, как, например, снежинка Коха или кривая Гильберта, до структур, очень напоминающих растительную или подводную жизнь.

По адресу inf.1september.ru/2000/6/fract/main.htm можно найти программы для моделирования L-фракталов, написанные на Q-basic и на C. Я, однако, написал собственный вариант программного кода на Visual Basic, который алгоритмически несколько отличается от программы, приведенной по указанному выше адресу.

На рисунке приведено несколько примеров фрактальных структур, построенных при помощи описанной программы.

Может ли быть случайным столь разительное сходство L-фракталов с формами живых организмов? Думается, что нет. Наверняка генетические программы развития растительных и подводных организмов имеют много общего с принципами описанного L-кодирования. С позиций L-формализма легко поддаются логическому объяснению и разнообразие биологических форм, и принципы их эволюции. Ведь для получения какой-либо новой формы достаточно лишь немного изменить какой-либо параметр или элемент исходной программы, сохранив при этом сам принцип построения. В то же самое время L-формализм демонстрирует всю несостоятельность статистических аддитивных подходов к описанию наследования фенотипических признаков организмов, которые до настоящего времени имеют сильное влияние в биологической науке. На примере L-фракталов можно проиллюстрировать конструктивный параллельный перенос эвристичных идей из разных областей знания. Думается, что фрактальная геометрия могла бы натолкнуть генетиков на решение многих загадок, связанных с природными принципами формообразования и наследования. Впрочем, справедливо и обратное. Недаром принцип L-кодирования был предложен не математиком, а именно биологом.

А. КОЛЕСНИКОВ,
andr61@mail.ru

* Чусовитин А.Г. Концепция деятельности (онтологический и методологический аспекты)\\ Полигнозис 4\2000, - с 149

Dim x_stack(200) As Single
Dim y_stack(200) As Single
Dim a_stack(200) As Single
Dim MaxDepth As Byte
Dim ProgramString As String
Dim NewProgramString As String
Dim Rule(10) As String
Dim RuleSimbol(10) As String
Dim Replace As Boolean
Dim Axiom As String
Dim Simbol As String
Dim Nrule As Byte
Dim angle As Byte
Dim R As Single

Private Sub Form_Click()
 Open "Растение 2.txt" For Input As #1
 Input #1, Axiom
 Input #1, angle
 Input #1, Nrule
 Input #1, MaxDepth
 For i = 1 To Nrule
  Input #1, RuleSimbol(i)
  Input #1, Rule(i)
 Next i
 Close #1
 R = 500
 Interpretation
 Visualisation
End Sub

Public Sub Interpretation()
 Depth = 0
 ProgramString = Axiom
 NewProgramString = ""
 Do While Depth <= MaxDepth
  For i = 1 To Len(ProgramString)
   Simbol = Mid$(ProgramString, i, 1)
   Replace = False
   j = 1
   Do While j <= Nrule
    If RuleSimbol(j) = Simbol Then
     Replace = True: Exit Do
    End If
    j = j + 1
   Loop
   If Replace Then
    NewProgramString = NewProgramString + Rule(j)
   Else
    NewProgramString = NewProgramString + Simbol
   End If
  Next i
  Depth = Depth + 1
  ProgramString = NewProgramString
  NewProgramString = ""
  R = R / 1.5
 Loop
End Sub

Public Sub Visualisation()
 Pi = 3.141592654
 x = 3000
 y = 0
 a = 0
 sector = (360 / angle) * Pi / 180
 Cs = 0
 PSet (x, 7000 - y)
 For i = 1 To Len(ProgramString)
  Simbol = Mid$(ProgramString, i, 1)
  Select Case Simbol
  Case "F"
   x = x + R * Cos(a)
   y = y + R * Sin(a)
   Line -(x, 7000 - y)
  Case "+"
   a = a - sector
  Case "-"
   a = a + sector
  Case "["
   Cs = Cs + 1
   x_stack(Cs) = x
   y_stack(Cs) = y
   a_stack(Cs) = a
  Case "]"
   x = x_stack(Cs)
   y = y_stack(Cs)
   a = a_stack(Cs)
   PSet (x, 7000 - y)
   Cs = Cs - 1
  End Select
 Next i
End Sub

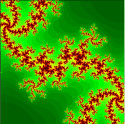
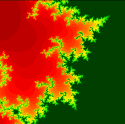
Визуализация фрактальных структур

"В один прекрасный день под поверхностью океана возникает темный плоский широкий круг с рваными краями и как бы залитый смолой. Через несколько часов он начинает делиться на части, все более расчленяется и одновременно пробивается к поверхности. Наблюдатель мог бы поклясться, что под ним происходит страшная борьба, потому что со всех сторон сюда мчатся похожие на искривленные губы, затягивающиеся кратеры, бесконечные ряды кольцевых волн громоздятся над разлившимся в глубине черным колеблющимся призраком..." Все написанное некогда Станиславом Лемом о невероятных образованиях, возникающих в недрах придуманного им мыслящего океана Соляриса, хорошо подходит к структурам фрактальных множеств Мандельброта и Жюлиа. Редкое математическое открытие в истории человечества удостаивалось столь широкой популярности. Сегодня изображения множества Мандельброта и множества Жюлиа можно встретить где угодно - на рекламных плакатах, обложках многочисленных книг, журналов и т.д. В мировом киберпространстве даже появились целые картинные галереи, поражающие своей завораживающей и странной красотой. Из-за бедных вычислительных возможностей человеческого мозга своеобразная красота этих множеств раньше была скрыта от наших глаз. Теперь же, использовав, к примеру, материал этой статьи, вы можете без особого труда создать собственный фрактальный "микроскоп" и попробовать свои силы в этой новой, недавно возникшей области компьютерного искусства.

Мы привыкли изображать объекты окружающего нас мира как некие сплошные тела с четко обозначенными границами. Но далеко не все формы в природе действительно таковы. Достаточно вспомнить, например, облака или морозные узоры на стеклах. Структуры подобного рода принято называть фрактальными. Множества Мандельброта и Жюлиа тоже представляют собой фрактальные объекты. Они не имеют ясно очерченных контуров. Вернее сказать, эти контуры настолько сложны, что мельчайшие их детали теряются в бесконечности. Последовательно увеличивая фрагменты множеств Мандельброта и Жюлиа, мы будем обнаруживать все новые и новые разнообразные "пейзажи" (см. рис.1 и рис. 2).

Рис. 1

Рис. 2

В этом состоит парадоксальная сущность природы фракталов. Благодаря своему бесконечно сложному строению фрактальные "кружева" имеют дробную (!) пространственную размерность. То есть они представляют собой нечто среднее между одномерными линиями и сплошными геометрическими фигурами.

Характерным свойством множеств Мандельброта и Жюлиа является самоподобие их отдельных деталей на разных масштабных уровнях рассмотрения. В отдельных фрагментах пограничных областей множества Мандельброта можно обнаружить многократно уменьшенные копии целого множества. Этот принцип иерархической организации широко распространен в природе и особенно ярко проявляется в мире биологических структур. Убедиться в этом можно, если внимательно рассмотреть лист любого растения или проанализировать форму строения органов (например, легких) у животных организмов. Возможно, в этом принципиальном подобии кроется секрет эстетической привлекательности фрактальных множеств

Умопомрачительная сложность структур множеств Мандельброта и Жюлиа порождается элементарной формулой:

Z_i+1=Z_i² + C (1),

где Z и C - комплексные числа. Это совсем не означает, что всякий раз вам придется непременно извлекать немыслимый мнимый корень из минус единицы. Используя правила сложения и умножения комплексных чисел, эту формулу легко заменить двумя традиционными математическими выражениями, не содержащими никаких мнимых сомножителей:

x_i+1=x_i² - y_i² + a, y_i+1=2x_iy_i + b. (2)

Суть метода построения множества Мандельброта состоит в следующем. Для каждого пиксела, отображающего некоторую точку с координатами (a, b), проводят серию вычислений по формулам (2). При этом исходные значения x₀ и y₀ для каждой новой точки (a, b) изначально всегда равны нулю. На каждом шаге, кроме очередных значений x_i+1 и y_i+1, вычисляют величину r_i=sqrt(x_i+y_i). Эта величина представляет собой не что иное, как расстояние от точки (x_i, y_i) до начала координат. Точка (a, b) считается принадлежащей множеству Мандельброта, если она в процессе вычислений никогда не удаляется от начала координат на критическое расстояние, большее или равное двум. Такой пиксел окрашивается в черный цвет. Для всех прочих значений a и b величина r_i может переходить запретный рубеж в две единицы за разное количество шагов. В зависимости от этого, точку окрашивают в соответствующий цвет.

Критическое значение при программировании фрактального "микроскопа" имеет скорость вычислений. Для того, чтобы работа с программой доставляла удовольствие, код нужно стремиться максимально оптимизировать. Существенно влияют на время расчетов операции возведения в степень и извлечение квадратного корня. Возведение в квадрат целесообразно заменить умножением. Возводить координаты в квадрат следует лишь один раз, сохраняя результаты в промежуточных переменных (X2 и Y2). От извлечения квадратного корня вообще следует отказаться. Вместо самого значения расстояния ri можно вычислять лишь сумму квадратов x²+y², сравнивая ее не с двойкой, а с четверкой.

Программные процедуры для генерации множества Мандельброта на языке Visual Basic приведены ниже. В зависимости от полученного значения k (обратного счетчика итераций), очередная точка закрашивается в соответствующий цвет (в данном случае точка окрашивается в различные градации серого цвета). Если k оказывается равным нулю, то точка с координатами (a, b) принадлежит множеству Мандельброта. В отношении всех прочих точек имеет значение, насколько велико или мало значение k. Оно характеризует скорость убегания величины ri за дозволенный предел при данных значениях a и b.

DefSng X-Z
DefInt I-N
Private Sub Command1_Click()
Dim c As Long
n = 525
xmin = text1(0).Text
xmax = text1(1).Text
ymin = text1(2).Text
ymax = text1(3).Text
hx = (xmax - xmin) / n
hy = (ymax - ymin) / n
x = xmin
y = ymin
For j = 0 To n
 For i = 0 To n
 c = Mandelbrot(x, y)
 x = x + hx
 Screen.PSet (i, j), c
 Next i
 y = y + hy
 x = xmin
Next j
End Sub

Public Function Mandelbrot(a As Single, b As Single) As Long
Dim k As Byte
x = 0
y = 0
k = 100
Do While r <4 And k> 0
 X2 = x * x
 Y2 = y * y
 xy = x * y
 x = X2 - Y2 + a
 y = 2 * xy + b
 r = X2 + Y2
 k = k - 1
Loop
k = (k / 100) * 255
Mandelbrot = RGB(k, k, k)
End Function

Полное изображение множества Мандельброта можно построить на участке координатной плоскости от -2 до 1 по оси x, и от -1,5 до 1,5 - по оси y (см. рис. 1). Предельное ограничение для количества итераций для одного пиксела задается произвольно. Известно, что для достижения вполне приемлемой точности достаточно 100 итераций. По традиции точки, остающиеся на расстоянии менее 2 единиц от начала координат в течение всех 100 итераций, принято окрашивать в черный цвет и считать принадлежащими множеству Мандельброта. В отношении всех прочих можно поступать как подсказывает интуиция и художественный вкус. Эстетическая привлекательность получаемых изображений очень зависит именно от удачного выбора того или иного цветового решения. Так, например, эффект протянутых в бесконечность полосатых "щупалец" (см. рис. 3) можно получить, окрашивая все точки, для которых число итераций k было четным, - в черный цвет, а те точки, для которых k было нечетное - в белый.

Рис. 3

С отображением (1) связано еще одно фрактальное множество - множество Жюлиа (рис. 4, 5).

Рис. 4

Рис. 5

При построении множества Мандельброта от пиксела к пикселу изменяется значение a и b. Начальные значения x0 и y0 всегда равны нулю. Если же наоборот, изменять значения x0 и y0, выбрав какие-то определенные значения a и b, то в результате получится множество Жюлиа. Множество Жюлиа, как и множество Мандельброта, обладает фрактальными свойствами. Для того, чтобы сгенерировать множество Жюлиа, требуется лишь незначительно модифицировать приведенную программу. Вызывающую процедуру можно оставить той же самой, заменив лишь обращение c = Mandelbrot(x, y) на c=Julia(x, y). В тексте самой подпрограммы-функции надо изменить заголовок и передаваемые параметры x и y принимать не как очередные значения a и b, а как очередные значения x0 и y0.

Public Function Julia(x0 As Single, y0 As Single) As Long
Dim k As Byte
Dim x2 As Single
Dim y2 As Single
Dim xy As Single
a = -0.55
b = -0.55
k = 100
x = x0
y = y0
Do While r <4 And k> 0
 x2 = x * x
 y2 = y * y
 xy = x * y
 x = x2 - y2 + a
 y = 2 * xy + b
 r = x2 + y2
 k = k - 1
Loop
k=(100 / k) * 255
Julia = RGB(k, k, k)
End Function

Мир фракталов не исчерпывается лишь рассмотренными множествами Мандельброта и Жюлиа. Просто они приобрели наибольшую известность у любителей программирования. Фракталы - это весьма обширный класс геометрических объектов. Многие очень интересные самоподобные фрактальные изображения, такие, как, например, треугольник Серпинского, можно получить, используя аффинные преобразования координат. На основе этого подхода ведется разработка методов невероятно эффективного кодирования произвольных изображений, позволяющих добиться сверхвысокой степени сжатия графической информации. Сжатие изображений является одним из наиболее интересных, но далеко не единственным направлением практического использования фрактальной геометрии. Кроме того, фракталы дают богатую пищу для философских размышлений о фундаментальных принципах устройства нашего мира. Исходя из "фрактальной" логики можно заключить, что природе вовсе не обязательно проявлять бесконечную изобретательность. Разнообразие форм, которое мы видим вокруг, в принципе может быть построено при помощи небольшого количества остроумных нелинейных соотношений, способных порождать сложные фракталоподобные структуры.

А.КОЛЕСНИКОВ

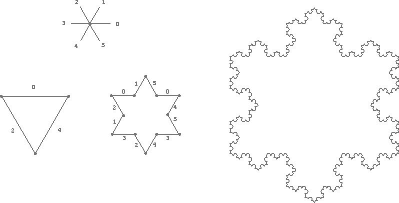
Как построить снежинку Коха

Фрактальная снежинка - один из самых известных и загадочных геометрических объектов - описана Хельгой фон Кох еще в начале нашего века. По традиции ее называют у нас в литературе снежинкой Коха. Это очень "колючая" геометрическая фигура, которую метафорически можно рассматривать как результат многократного "умножения" звезды Давида на саму себя. Шесть ее основных лучей покрыты бесконечным количеством больших и малых вершин-"иголочек". Всякий микроскопический фрагмент контура снежинки как две капли воды похож на весь большой луч, а большой луч в свою очередь содержит в себе бесконечное количество таких же микроскопических фрагментов.

На международном симпозиуме по методологии математического моделирования в Варне еще в 1994 году мне на глаза попалась работа болгарских авторов, которые описывали свой опыт использования снежинки Коха и других подобных объектов на уроках в старших классах для иллюстрации проблемы делимости пространства и философских апорий Зенона. Помимо этого, с образовательной точки зрения весьма интересен, на мой взгляд, сам принцип построения регулярных фрактальных геометрических структур - принцип рекурсивного умножения базового элемента. Природа недаром "любит" фрактальные формы. Это объясняется именно тем, что они получаются путем простого размножения и изменения размеров некого одного элементарного строительного блока. Как известно, природа не излишествует разнообразием причин и, где возможно, обходится наиболее простыми алгоритмическими решениями. Присмотритесь внимательно к контурам листьев, и во многих случаях вы обнаружите явное их родство с формой контура снежинки Коха.

Визуализация фрактальных геометрических структур возможна лишь при помощи компьютера. Построить снежинку Коха выше третьего порядка вручную уже очень сложно, а заглянуть в бесконечность так хочется! Поэтому, почему бы ни попытаться разработать соответствующую компьютерную программу. В РуНете можно отыскать рекомендации строить снежинку Коха из треугольников. Результат работы этого алгоритма выглядит как нагромождение пересекающихся линий. Интереснее скомбинировать эту фигуру из "кусочков". Контур снежинки Коха состоит из отрезков одинаковой длины, наклоненных под углом 0°, 60° и 120° по отношению к горизонтальной оси x. Если обозначить их соответственно 1, 2 и 3, то снежинка любого порядка будет состоять из следующих друг за другом троек - 1, 2, 3, 1, 2, 3, 1, 2, 3… и т. д. Каждый из этих трех типов отрезков может прикрепляться к предыдущему одним либо другим концом. С учетом этого обстоятельства можно считать, что контур снежинки состоит из отрезков шести типов. Обозначим их 0, 1, 2, 3, 4, 5. Таким образом, мы получаем возможность кодировать контур любого порядка при помощи 6 цифр (см. рисунок).

Снежинка более высокого порядка получается из предшественницы более низкого порядка путем замены каждого ребра на четыре, соединенных подобно сложенным ладошкам (_/\_). Ребро типа 0 заменяется на четыре ребра 0, 5, 1, 0 и так далее в соответствии с таблицей:

Простой равносторонний треугольник можно рассматривать как снежинку Коха нулевого порядка. В описанной системе кодировки ему соответствует запись 0, 4, 2. Все остальное можно получить путем описанных замен. Я не буду приводить здесь код процедуры и тем самым лишать вас удовольствия разработать свою программу самостоятельно. При ее написании вовсе необязательно использовать явный рекурсивный вызов. Его можно заменить обычным циклом. В процессе работы у вас будет лишний повод поразмыслить о рекурсии и ее роли в образовании квазифрактальных форм окружающего нас мира, а в конце пути (если, конечно, не поленитесь пройти его до конца) вы сможете полюбоваться сложным узором контуров фрактальной снежинки, а также заглянуть, наконец, в лицо бесконечности.

А. КОЛЕСНИКОВ,
andr61@mail.ru

Сложность и красота

Атмосфера Юпитера представляет собой, наверное, одно из самых захватывающих зрелищ в Солнечной системе. Между ледяным холодом космического пространства и тысячеградусной жарой в глубинах атмосферного океана гигантской планеты зарождаются циклопические облачные вихри самых причудливых форм (см. рис. 1).

Рис. 1

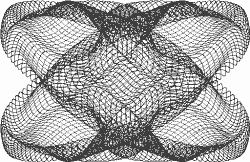
Зоны турбулентности обрамляют загадочные устойчивые структуры типа знаменитого красного пятна - ни с чем земным не сравнимая по своей мощи и масштабам величественная и бесцельная игра формотворящих сил природы. Заурядный юпитерианский вихрь мог бы, наверное, запросто поглотить весь наш земной мир, не претерпев при этом существенных изменений. К вызывающим восхищение и трепет эволюциям юпитерианских облачных масс в равной степени приложимы такие понятия, как "сложность" и "красота". Герменевтика - одно из ведущих направлений в современной западной философии - утверждает, что истинный смысл понятий уже скрыт в самом естественном языке, нужно лишь суметь его увидеть и расшифровать. Естественные языки базируются на веками отшлифованных интуитивных конструкциях, которые, зачастую, адекватнее отображают истину, нежели любые искусственные теоретические построения. Понятия "сложность" и "красота" относятся к тем базовым конструкциям языка, которые совершенно бесполезно пытаться определить через что-то иное. В этих попытках мы обязательно упремся в тавтологию или более узкий синоним. В структуре русского языка в понятие "сложность" вплетено представление о складывании, сложенности, сложении, складке. Что, кстати, вполне соответствует юпитерианским облачным пейзажам. В самой ассоциативной основе слова заложены принципы складывания, многократного перегибания, вложения одного в другое.

Недавно, просматривая старые номера журнала "В мире науки" (русское издание известного научно-популярного журнала Scientific American (http://www.sciam.com/), которое было успешно похоронено в развалинах перестройки), я наткнулся на описание кривой под названием "Безумие". Кривая была случайно получена в процессе любительских опытов С. Миллером и описана А.К. Дьюдни в рубрике "Занимательный компьютер" (см. А.К. Дьюдни. Графотворчество невидимого профессора, скрытого за экраном дисплея// В мире науки - 1988/№7). Ее сложные и красивые формы побудили меня воспроизвести "Безумие" на своем компьютере по приведенным в статье параметрическим уравнениям (рис. 2).

Рис. 2

Форму этой кривой, несомненно, можно определить как сложную. Но в то же время она строится по единому закону при помощи совсем нехитрого программного кода.

Dim i As Integer
Dim j As Integer
Sub Form_click()
 Cls
 pi = 3.141593
 For t = 0 To 100 * pi Step 0.001 * pi
  x = Sin(0.99 * t) - 0.7 * Cos(3.01 * t)
  y = Cos(1.01 * t) + 0.1 * Sin(15.03 * t)
  i = 150 * x + 300
  j = 150 * y + 300
  PSet (i, j)
 Next t
End Sub

Рассматривая изображения сложных кривых, мы далеко не всегда можем угадать тот закон, по которому они построены, но всегда интуитивно ощущаем его присутствие. Оно проявляется в гармонии форм, симметрии и порядке. Не вполне адекватно было бы употреблять эпитет "сложный" по отношению, например, к мотку спутанных кабелей, но по отношению к умопомрачительному переплетению проводов в недрах корпуса суперкомпьютера он более чем уместен. Понятие "сложность" предполагает не столько простое случайное нагромождение деталей, сколько упорядоченную структуру, подчиненную некой единой внутренней логике. Кривая Миллера не только сложна, но и красива. Рассматривая ее, получаешь отчетливое эстетическое наслаждение. То же самое можно сказать и о сложных нелинейных поверхностях, о которых велась речь в некоторых моих прошлых статьях (№29 1999 г., №2 2000 г. и №13 2000 г.). Таким образом, сложность внутренне связана с красотой. Когда множество деталей картины или литературного текста гармонично объединены общей идеей, все произведение воспринимается, в целом, как красивое. Чем глубже идея, лежащая в основе произведения искусства, чем адекватнее использованные автором художественные средства выражают эту идею, тем выше эстетическая ценность всего произведения. Разница состоит в том, что кинолента, картина или стихотворение обычно базируются не на математических законах, а на законах философских, этических или нравственных. Интересно, что при замене гуманитарной идеи на математическую закономерность человеческое антропоморфное восприятие феномена красоты сохраняется, и само понятие "красиво" оказывается вполне применимо к таким формально далеким от искусства геометрическим объектам, как кривые и поверхности.

Впрочем, математические закономерности играют немаловажную роль и в традиционных искусствах. В живописи используются гармоничные сочетания цветов и геометрия перспективных проекций. Музыка воспринимается как музыка только в том случае, если частоты звуков находятся в определенных взаимных математических соотношениях друг с другом. Поэтому музыкальные пьесы и стихи, созданные при помощи компьютерных программ, в которые заложены лишь соответствующие математические закономерности, в принципе, воспринимаются именно как музыка и стихи. Художественное качество этих произведений, конечно, весьма спорно, но факт их восприятия именно как произведений искусства не вызывает сомнений.

В принципе, красоту можно определить как эмоциональное измерение сложности, как специфику человеческого восприятия сложности. Одним из фундаментальных принципов, на котором базируется феномен сложности, является рекурсия. В основе большинства сложных структур лежат именно рекурсивные принципы построения. В моих прошлых статьях в "КВ" приводились изображения нескольких известных геометрических объектов - Снежинки Коха, Драконовой ломаной и треугольника Сиерпинского. К их форме в равной степени приложим эпитет - "сложная". Причем сложность этих объектов возрастает по мере увеличения порядка. Все они относятся к рекурсивно порождаемым самоподобным геометрическим структурам. Мы уже говорили о том, что в самой ассоциативной основе русского слова "сложность" или, например, белорусского аналога "складанасць" заложен принцип складывания, закладки одного в другое, плотной упаковки некоего многократно сложенного целого. Перечисленные объекты как нельзя лучше подходят под этот ассоциативный ряд. Драконова ломаная, например, есть не что иное, как многократно сложенный прямым углом отрезок. Снежинка Коха - есть не что иное, как многократно скомканный контур звезды Давида. Треугольник Сиерпинского - это многократно вложенный сам в себя треугольник. При этом "складанасць", или сложность перечисленных объектов представляет собой результат многократного применения некоего элементарного рекурсивного алгоритма "складывания" к некоей простейшей изначальной геометрической основе. Эти примеры как нельзя лучше иллюстрируют понятия "сложность" - лаконичная общая идея и составной результат с обилием деталей, но деталей не случайных, а порожденных единой логикой организации объекта.

Настоящим зримым воплощением понятия "сложность" являются комплексные фрактальные множества Мандельброта и Жюлиа. Порождаемые элементарным нелинейным отображением фрактальные структуры комплексных множеств так много говорят о философских принципах устройства нашего мира, что кто-то из ученых метко назвал их отпечатком большого пальца Бога. Их формы сколь сложны, столь и великолепно красивы. По существу, одна математическая формула породила целое направление в изобразительном искусстве - фрактальное искусство. В Сети выставлено множество фрактальных галерей, содержащих сотни живописных компьютерных произведений. Заинтересованный читатель может сам попробовать свои силы в этой области, воспользовавшись несложными программными кодами, приведенными в моих статьях ("КВ" №16, 1999 г. и №2, 2000 г. Изображения, приведенные на рисунках 3 и 4, получены именно при помощи этих программ).

Рис. 3	Рис. 4

Тот факт, что сложные геометрические структуры способны вызывать сильные эстетические чувства, убедительно свидетельствует в пользу тезиса о том, что сложность и красота - родственные по своей природе и смысловому содержанию понятия. Кроме того, сложность и красота представляют собой не только чисто субъективные гуманитарные характеристики предметов. Они имеют под собой и определенные объективные математические корни. Давно замечена, например, связь красоты и знаменитого соотношения золотого сечения. Кстати сказать, определение золотого сечения также основано на рекурсивной идее бесконечного деления отрезка. Есть все основания надеяться, что изучение феноменов нелинейности и фрактальной геометрии приблизят нас к более глубокому пониманию природы сложности и природы красоты. По выражению московского философа В.И. Самохваловой, "мудрость красоты в том, что она есть интуитивное постижение самой сути вещи в логике ее проявления, в совершенстве той организации вещи, которая отвечает закономерностям ее развития" (цит. по Самохвалова В.И. Красота против энтропии. - М.: Наука, 1990. - с.79).

А. КОЛЕСНИКОВ,
andr61@mail.ru

Фракталы, рекурсия и эволюция

Одна из самых сокровенных загадок природы - это тайные механизмы эволюционных изменений живых организмов. Синтетическая теория эволюции (современный вариант синтеза классического дарвинизма и генетики) довольно скупо констатирует, что случайные мутационные изменения фильтруются естественным отбором, и постепенно, из хаоса неопределенной изменчивости, выкристаллизовываются совершенные формы, идеально приспособленные к своим условиям обитания. Эта, в общем, правдоподобная теоретическая картина несколько расходится с данными палеонтологической летописи, которая оказалась достаточно прерывистой. Из данных раскопок следует, что новые формы живых организмов появлялись, скорее, скачкообразно, нежели путем последовательной "шлифовки", как того требует классическая теоретическая схема.

Как же так может быть, чтобы столь органичная и высоко интегрированная система, как живой организм, вдруг изменилась бы скачком, да еще и без потери своей функциональности. Принципиальный ответ на этот вопрос можно получить, проводя несложные компьютерные опыты с фрактальными геометрическими фигурами. Еще Гете заметил, что формы живых организмов построены, выражаясь современным языком, по рекурсивному, квазифрактальному принципу. Все части живых организмов несут в себе черты самоподобия, а многие биологические структуры имеют откровенные фрактальные формы. Да и сам процесс индивидуального развития живого организма с информационной точки зрения можно рассматривать как реализацию сложного рекурсивного алгоритма. С учетом этого обстоятельства скачкообразные трансформации биологических объектов в процессе филогенеза уже не кажутся столь чудесными. Ведь в рекурсивно организованных фрактальных структурах достаточно совсем незначительно изменить код исходного первокирпичика, чтобы в результате его самоповторения получилась бы совсем иная конечная форма.

Проиллюстрируем это явление на примере уже упоминавшейся нами ранее на страницах "КВ" снежинки Коха (см. "КВ" №49 от 7 декабря 2000 года). Напомним, что снежинка Коха "рождается" из треугольника. На каждом последующем шаге все стороны фигуры заменяются фрагментом, показанным на рисунке. Снежинка Коха первого порядка - это небезызвестная звезда Давида. Затем после каждого последующего цикла замен она все больше и больше начинает напоминать снежинку с множеством боковых иголочек. В исходных данных рекурсивной программы, строящей снежинку Коха, достаточно поменять местами всего два символа для того, чтобы в результате ее работы появилось нечто совершенно иное, но не менее сложное и интересное. Эта "мутация" приводит к тому, что лучи оказываются вывернутыми не наружу, а вовнутрь. Таким образом, после первого цикла рекурсивных замен из исходного треугольника получается уже не звезда Давида, а логотип фирмы Mitsubishi. "Мутант" четвертого порядка представлен на рисунке. Он совсем не похож на снежинку Коха, хотя определенное родство между этими фигурами, несомненно, прослеживается.

Компьютерное моделирование таких, на первый взгляд, несложных алгоритмических задачек часто позволяет глубже понять и проиллюстрировать суть сложных природных процессов, даже таких нетривиальных и загадочных, как мутационная изменчивость биологических организмов. Один из основных общих выводов, которые можно сделать, опираясь на некоторые открытия последних десятилетий в области нелинейной динамики и фрактальной геометрии, состоит в том, что простые, строго детерминированные, "механические" законы способны порождать бесконечно сложные структуры. Применительно к проблеме эволюции этот вывод имеет принципиальное теоретическое значение. Вовсе необязательно, чтобы сложные формы порождались бы сложными закономерностями. Если бы это было так, то биологическая эволюция вообще вряд ли могла быть возможной. Принципы фрактальной организации сложных структур снимают проблему. С позиции рекурсивного устройства легко объясняется и феномен мутационной изменчивости, и феномен индивидуального развития, что с традиционных "досинергетических" представлений объяснить было невозможно. Такая сложная алгоритмическая задача, как биологическая эволюция, и не могла быть решена иным способом, кроме рекурсии. Невозможно было сразу "создать" совершенные сложные живые формы. Потребовались миллионы лет генетических "вычислений" для того, чтобы получились наблюдаемые нами результаты (включая, конечно, и самих наблюдателей). Начиная с простейших каоцерватных капель, несколько миллиардов лет природа "раскручивала" усложняющиеся, самонастраивающиеся генетические коды, которые несли в себе все более сложные программы построения соматических структур. Форма организации этих структур неизбежно и повсеместно несет в себе следы рекурсивных процедур, которые зримо воплотились в квазифрактарных формах соматических структур живых организмов.

А. КОЛЕСНИКОВ,
andr61@mail.ru