Четыре шага к новому искусству часть 1 Опубликовано в журнале Hard'n'nSoft №12 2001 Стр. 88

Для оптимальной загрузки статья разбита на 2 части:
Шаг первый. Плитки и шизофрения  и Шаг второй. Шестилапые и анимация читайте на этой странице. 
Шаг третий. В гостях у профессора Пола Брауна и Шаг четвертый. Искусство нового века смотрите здесь. 
Также посетите Вернисаж изображений, в том числе и Пола Брауна.

- Все Пластилины Мира - лжецы. Кроме меня, - причем  на середине фразы из пляжного старика он превратился в прехорошенькую девушку, так что осталось неясным, к кому из них относится послед­няя часть высказывания.
- Здравствуйте, - на всякий случай сказал Петропавел, с восхищением глядя на девушку. - Виделись уже, - улыбнулась та и протянула ему руку: - Пластилин Мира. - Петропавел пожал руку. Рука осталась у него в кулаке. С ужасом и отвращением он бросил руку на пол. Девушка подняла ее и приставила на прежнее место: - Фу, неаккуратный какой! Осторожнее надо...
Е.В.Клюев. Между двух стульев  

Любители математики знают, как она (математика) красива. Среди скучнейших выкладок вдруг выявится изящное уравнение, график замысловатого процесса нарисует вдруг цветочный узор, или, бывает, что красива сама формулировка задачи. А уж с компьютером на столе – для таких любителей разговор особый. 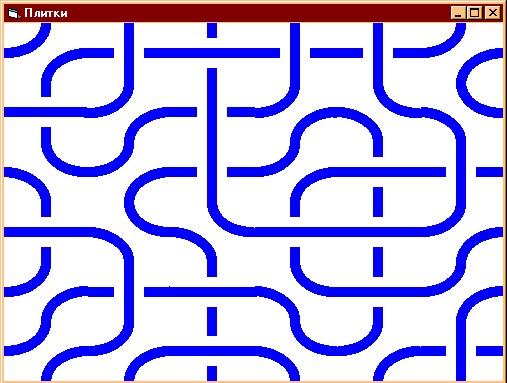Признанный ускоритель процессов в любой области его применения - он волшебным образом расширяет круг приятных задач, преподносит новые, неисследованные модели.
Первопроходцем компьютерных математических забав (наряду с Дж. Конвеем, придумавшем игру «Жизнь») считается Клиффорд Пикоувер, основатель, если можно так выразиться, компьютерного построения организмов и методов визуализации информации. Еще в конце 1980-х годов журнал «Scientific American» («В мире науки» 9/1989) рассказывал об этом ученом и о биоморфах - фрактальных картинках, похожих на живые организмы. Его страничка в Интернете (http://sprott.physics.wisc.edu/pickover/home.htm ) открывается  цитатой из «Лос-Анджелес Таймс»: «Доктор Пикоувер своими публикациями ежегодно раздвигает наши границы в области компьютеров, искусства и мышления».

Шаг первый. Плитки и шизофрения 

Тот же журнал двенадцатилетней давности поведал об одном из "чудачеств" Пикоувера - предложенном им методе визуализации информации с помощью так называемых "плиток Трюше", названных так в честь французского монаха и энциклопедиста Себастьяна Трюше, жившего в XVII веке, и наверняка знакомые любителям математики. Плитки состоят из двух четвертей круга в квадрате; центры круговых секторов находятся в противоположных углах квадрата, а ограничивающие их радиусы совпадают с двумя сторонами квадрата. Получающаяся в результате плитка (см. рис.) может иметь только две различных ориентации. 

Используя эти плитки можно преобразовать в узор любой набор битов, располагая на плоскости плитку, ориентированную одним способом, если пришел ноль и другим, если единица. Если заполнить плоскость, выбирая ориентацию плиток случайным образом, то мы получим хаотический (но от этого не менее красивый) узор. В нем лабиринты замысловатых цепочек соседствуют с одиночными кругами, двойными гантельками, тройными, четверными (и т.д.) замкнутыми областями. Картинка красива сама по себе, но, не менее красивы порождаемые ею сопутствующие занимательные задачи. Ознакомиться с ними можно в статьях Бульон из информации и Визуализация... Однако, вся изюминка состоит в том, что упорядоченный сигнал разумного происхождения дает картинку, отличную от картинки хаотического шума. Конечно, эстетическое восприятие картинок субъективно, каждый видит по-своему. Но, тем более, это дает простор в поисках закономерностей, в определении "разумности" источника сигнала. Используя плитки каждый желающий может попытаться отыскать сигналы внеземного разума, конкурируя с известным Интернет-проектом SETI@home поиска разумных сигналов из Космоса с помощью распределенных вычислений www.setiathome.ssl.berkeley.edu. Здесь, также, возникают интересные вопросы о совпадении понятия разумности нашего и "отправителей" сигнала, и о случайности тех или иных явлений. Например, соотношение плохих и хороших событий в теленовостях, карканье ворон, применение ненормативной лексики или прерывание фильма для рекламы - случайно ли это распределено во времени или несет в себе высокоразумную информацию? Вопрос для читателей с развитым воображением - как изменится картина, если поменять местами плитки, соответствующие нулю и единице соответственно? Сохраниться ли просматриваемая "разумность" сигнала"? 

Предложенная модель не только красива сама по себе, но и предоставляет простор для приятных опытов. Первым делом картинку следует оживить. Для этого в замощенной плитками поверхности выбираем плитку (случайным образом или по какому-либо алгоритму) и меняем (или не меняем) ее ориентацию случайным образом или в зависимости от используемого нами источника сигналов. Подобрав оптимальную величину задержки для своего компьютера, вы будете поражены происходящим на экране - на нем бурлит, кипит, живет (и вопиет) самая, что ни на есть информация. 

Следующим шагом можно предложить заливать рисунок, начиная с какой-либо плитки, например, с центральной, меняя цвет после нескольких изменений ориентации плиток. Тоже получится удивительная картина - заливаться цветом будет то шарик, то гантелька, то, вдруг почти весь рисунок. Есть гипотеза, что длительное наблюдение за меняющимся узором Трюше способно донести до зрителя содержащуюся в потоке данных информацию. Тем более, что, по словам Шри Ауробиндо, человеческий мозг не генерирует мысли сам, а лишь транслирует их как телевизор, получая из внешнего поля неизвестной пока природы. Поразмышляйте об этом, не останавливаясь, однако, в наших экспериментах. Добавляем две плитки третьей - квадратом, у которого соединены середины противоположных сторон, это позволит разрядить сплошные повороты прямыми участками. Но это внесет в нашу картину точки пересечения линий, это не очень-то красиво. Поэтому мы добавим не одну, а две плитки с "крестиком" - в одной из них вертикальная линия проходит "над" горизонтальной, а в другой - горизонтальная "над" вертикальной. Запустив "процесс" получим невероятно красивую жизнь на кране - множество линий, замыкаясь-размыкаясь, поворачивая и распрямляясь, пытаются то соединить противоположные стороны экрана, то загибаются к его краям, возвращаются или замыкаются. 

Для тех, кому наблюдение красивой картинки не достаточно для ощущения полноты жизни, приведем варианты применения полученной модели. Первый вариант - предположим, что в системе (организме или предприятии), находящейся в равновесии все линии прямые и сигналы проходят беспрепятственно. При внесении возмущений линии начинают искривляться, сигналы проходят хуже (шизофрения?). В крайнем положении линии вырождаются в маленькие окружности, сигналы не проходят. Такая модель может быть применима к реальным процессам. Можно теперь задать параметры "стремления" системы вернуться (по принципу Ле Шателье) к начальному состоянию и параметры вносимых возмущений и наблюдать переходные процессы "живьем", ожидая равновесия на каком-либо уровне или, наоборот, того, что система пойдет вразнос (например, финансовый кризис, смерть или взрыв). Возможно, что визуализация процесса позволит выявить негативные тенденции на начальном этапе и своевременно принять меры для стабилизирования системы. Второй вариант. Лет пятнадцать назад в "Науке и жизни" была статья о том, что процесс мышления сводится к прорастанию временных связей между отдельными участками мозга. У кого-то они прорастают быстро, а у кого-то плутают и путаются. Особенно после третьей рюмки. Лучшей иллюстрации этой гипотезы, чем наши линии не найти... Для желающих лично насладиться процессом и исследовать многочисленные эффекты, возникающие при замене параметров приведем текст программы на Visual Basic. 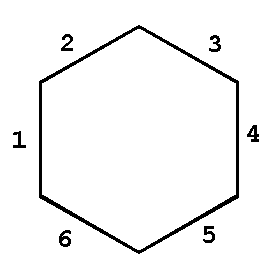От вас требуется только создать форму, назвать ее "Плитки" и "кинуть" на нее таймер.

Dim pi, i, j, k, r, n, x, y 
Private Sub Form_Load() 
Randomize (Timer) 
n = 5 'Количество плиток по вертикали и по горизонтали 
x = ScaleWidth / (n + 1) 
y = ScaleHeight / (n + 1) 
pi = 4 * Atn(1) 
For i = 0 To n 
    For j = 0 To n 
    draww 
Next j, i 
End Sub Private 
Sub Form_KeyPress(keyascii As Integer) 
    If keyascii = 32 Then End 'Если нажать пробел, то выход 
End Sub 
Private Sub draww() 'Подпрограмма рисования плитки 
Плитки.DrawWidth = 1 
' Очистка предыдущего изображения 
Line (x * i, y * j)-Step(x, y), RGB(255, 255, 255), BF 
Плитки.DrawWidth = (x + y) / 15 'Толщина линии 
If ScaleWidth > ScaleHeight Then 
    r = x / 2 
Else
   r = y / 2 
End If 
Select Case Int(Rnd * 4) 
Case 0 
    Circle (x * i, y + y * j), r, RGB(0, 0, 250), 2 * pi, pi / 2, y / x 
    Circle (x + x * i, y * j), r, RGB(0, 0, 250), pi, 3 * pi / 2, y / x 
Case 1 
    Circle (x + x * i, y + y * j), r, RGB(0, 0, 250), pi / 2, pi, y / x 
    Circle (x * i, y * j), r, RGB(0, 0, 250), 3 * pi / 2, pi * 2, y / x 
Case 2 
    Line (x / 2 + x * i, y * j)-Step(0, y), RGB(0, 0, 250) 
    Line (x / 2 - 10 + x * i, y / 2 - 10 + y * j)-Step(20, 20), RGB(255, 255, 255), BF 
    Line (x * i, y / 2 + y * j)-Step(x, 0), RGB(0, 0, 250) 
Case 3 Line (x * i, y / 2 + y * j)-Step(x, 0), RGB(0, 0, 250) 
    Line (x / 2 - 10 + x * i, y / 2 - 10 + y * j)-Step(20, 20), RGB(255, 255, 255), BF 
    Line (x / 2 + x * i, y * j)-Step(0, y), RGB(0, 0, 250) 
End Select 
End Sub Private 
Sub Часы1_Timer() 
    x = Плитки.ScaleWidth / (n + 1) 
    y = Плитки.ScaleHeight / (n + 1) 
    i = Int(Rnd * (n + 1)) 
    j = Int(Rnd * (n + 1)) 
draww 
End Sub 

Шаг второй. Шестилапые и анимация. 

Пока набирайте программу (если лень - пишите, вышлю), а мы движемся дальше. Самый плодотворный прием вдохнуть вторую жизнь в процессы, протекающие на клетчатой доске - это перенести их на доску, состоящую из многоугольников другого типа, лучше всего шестиугольников. Известны шестиугольные шахматы (разные варианты), шашки, можно попробовать запустить "Жизнь", назначив толковые правила существования организмов. Мы же рассмотрим только шестиугольный аналог плиток Трюше, то есть проведем линии, соединяющие середины сторон шестиугольника. 

Сразу возникает вопрос - сколько существует вариантов таких плиток? Не так уж и много - ведь проводя одну линию, мы убираем из дальнейшего рассмотрения вариантов сразу две стороны, оставляя для второй линии всего три варианта, а для третьей линии выбора нет - она соединит оставшиеся несоединенные грани. Варианты можно свести в таблицу, представляя линии номерами сторон, которые она соединяет. В правой колонке покажем три цифры, показывающие, сколько вершин шестиугольника обходит каждая линия.

Таким образом, получили все возможных 15 вариантов проведения линий в шестиугольнике. А сколько же получится вариантов, если считать одинаковыми варианты, переходящие друг в друга при повороте и отражении? Для этого рассмотрим значения из правого столбца с учетом того, что очередность цифр не имеет значения, то есть варианты 221 и 212 равноправны. И получим всего пять уникальных вариантов, из которых вращением или отражением можно получить все пятнадцать вариантов. 

№	Количество обходимых вершин	Количество случаев	Рисунок
1	111	2
2	113	3
3	122	6
4	223	3
5	333	1

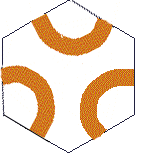
Шикарный вопрос для тех, кто думает, что что-то понял: почему нет в количестве обходимых вершин варианта 112? Приведенные выкладки не претендуют на академическую непогрешимость, просто рассуждения на досуге, буду рад, если кто-нибудь найдет ошибку или неточность. Во всяком случае, мы получили сведения о том, какая конфигурация линий в шестиугольных плитках встречается чаще всего, - при которой одна линия соединяет середины смежных сторон, а две другие линии, пересекаясь, соединяют середины сторон несмежных.

Дальнейшие наши действия? Ладно, сжалюсь - не будем больше писать программ - это утомительное и неблагодарное занятие. Ну кто сейчас пишет программы, когда полно готовых на все случаи жизни? А уж креативом (как сейчас модно говорить) занимаются все поголовно. Для наблюдения за жизнью наших шестиугольников с внутренними линиями создадим движущуюся картинку. Сначала в Corel Draw нарисуем шестиугольник, чтобы он был правильным, при движении мыши надо удерживать Alt, впрочем, читатели наверняка это знают. Потом рисуем "карандашом" внутренние линии и, двигая мышкой их узлы, добиваемся плавности. Когда шестиугольник готов копируем его и заполняем копиями плоскость.

Дальше у нас два варианта действий. Первый - сохранить полученный рисунок в формате GIF и открыть его в гиф-аниматоре, самый популярный из которых Ulread GIF Animator. Потом вернуться в Corel Draw, повернуть два-три шестиугольника на 60, 120, 180 или 240 градусов, запомнить картинку, зайти в гиф-аниматор и поместить ее во второй кадр. Повторять эти действия до получения приемлемой движущейся картинки. Объем ограничен только желанием разместить это чудо на своей страничке в Интернете. Второй путь - воспользоваться устанавливаемой вместе с Adobe Photoshop 6.0 специальной программой для создания гиф-анимации Adobe ImageReady. При описании любого программного продукта от любой фирмы непременно присутствует магическая фраза о том, что с каждой новой версией происходит все боле полная интеграция с ВЕБ, усиливается ориентация на ВЕБ. Данная программа как раз и является материализацией этих заклинаний, так как объединяет мощь Photoshop'a, признанного лидера в наборе инструментов художников всех мастей, с удобным средством создания компактных движущихся картинок. Особенно удобно создавать движение, делая для каждого кадра видимым только один слой. При сохранении картинки в каждом кадре запоминаются только его отличия от фоновой картинки, что позволяет получать картинки малого объема, а это важно для выкладывания их в Сеть. 

Наблюдение шестиугольников рождают вопрос, не относящийся непосредственно к сегодняшней теме - какой алгоритм шагания у шестилапых животных? (Известных, например, по книге А. Волкова "Семь подземных королей"). Если шагать медленно, то вроде ясно, то одна тройка ног, то другая, очень устойчиво. А если бежать - как будет выглядеть рысца или галоп с шестью копытами? 

Шаг третий. В гостях у профессора Пола Брауна и Шаг четвертый. Искусство нового века смотрите здесь.