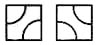Бульон из информации

Чаще всего выдумывают действительность.
(Мудрость, найденная в Интернете)

Из всевозможных применений компьютера для меня самым важным является волшебная возможность видеть на экране результат всяких математических фантазий. Знаете ли вы уравнение цветка сирени или листка крапивы? Их можно найти довольно быстро, набросав программку и просматривая картинку на экране. А о том, чтобы построить множество Мандельброта без компьютера не может быть и речи. Правда, игру «Жизнь» можно изучать на шахматной доске (чем я в детстве и занимался частенько), но, согласитесь, это исключение. Только на экране мы можем насладиться ростом кристаллов, полетом пружинки, фрактальными организмами, пеной и роением мошкары у фонаря – поменять формулы и параметры и, наконец, убедиться в своих догадках и заблуждениях. Отдельное место в подобных «забавах» занимает попытка определения смыслового содержания каких-либо данных по их внешнему виду. Самым ярким примером может служить так называемая «Скатерть Улама»: если числа подряд выписывать по спирали, то простые числа расположатся вдоль прямых линий, что довольно неожиданно.
Сегодня же хотелось бы рассказать об увиденном (и сразу запросившемся на экран) в старом журнале «В мире науки» (№9 1989 год.) интересном методе «визуализации» информации с помощью так называемых «плиток Трюше», названных так в честь французского монаха и энциклопедиста Себастьяна жившего в XVII в. Плитки состоят из двух четвертей круга в квадрате; центры круговых секторов находятся в противоположных углах квадрата, а ограничивающие их радиусы совпадают с двумя сторонами квадрата. Получающаяся в результате плитка (см. рис.) может иметь только две различных ориентации.

Используя эти плитки можно преобразовать в узор любой набор битов, располагая на плоскости плитку, ориентированную одним способом, если пришел ноль и другим, если единица. Если заполнить плоскость, выбирая ориентацию плиток случайным образом, то мы получим хаотический (но от этого не менее красивый) узор. (Смотри фон экрана) В нем лабиринты замысловатых цепочек соседствуют с одиночными кругами, двойными гантельками, тройными, четверными (и т.д.) замкнутыми областями. Картинка красива сама по себе, но, не менее красивы порождаемые ею задачи. Всегда ли, ткнув в картинку наугад, можно пройти в лабиринте до ближайшего края? Если нет, то какова вероятность успеха? Какова вероятность попасть в замкнутую область, или, лучше, каких областей больше – замкнутых, или проходных? Какова доля единичных шариков? Есть мнение, что она составляет 0.054 от полного числа плиток. А двойных и тройных? Сколько вариантов «пятикружковых» областей? Совпадает ли это с количеством вариантов предельных углеводородов? Обязательно ли любая кривая, не выходящая на границу площадки, должна быть замкнутой? Рассмотрите этот замечательный хаотический узор и вы найдете в нем много удивительных закономерностей.
Однако, вся изюминка состоит в том, что упорядоченный сигнал разумного происхождения дает картинку, отличную от картинки хаотического шума. Конечно, эстетическое восприятие картинок субъективно, каждый видит по-своему. Но, тем более, это дает простор в поисках закономерностей, каждый может попытаться отыскать сигналы внеземного разума, конкурируя с известным Интернет-проектом. Здесь, также, возникают интересные вопросы о случайности тех или иных явлений. Например, кваканье лягушек в озере, применение ненормативной лексики или прерывание фильма для рекламы – случайно ли это распределено во времени или несет в себе высокоразумную информацию?
А где же обещанный в заглавии бульон. Дело в том, что написать и запустить программку, заполняющую плоскость плитками Трюше в зависимости от какой-либо информации или случайным образом не так уж сложно (если лень - пишите – вышлю), но статичная картинка надоедает. И тут мы делаем великую вещь – оживляем ее (картинку). Для этого в выбранных случайно (или разумно) нарисованных уже плитках мы меняем (или не меняем – в зависимости от источника информации) ориентацию плитки. Подобрав оптимальную величину задержки для своего процессора вы заставите ахнуть от восторга любого, кто взглянет на экран: на нем бурлит, кипит, живет (и вопиет) самая что ни на есть информация.
И еще один способ качественного улучшения «визуализации» информации. Интересная картина получится, если узор Трюше заливать каким-либо цветом, начиная из случайно выбранной точки. Результат непредсказуем: может закраситься одна окружность, а может целый лабиринт или ажурная гирлянда. При повторении операции заливки случайных областей случайным цветом получим замысловатый узор, по виду которого также можно будет отличить случайный набор нулей и единиц от какой-либо осмысленной информации. Некоторые из полученных картинок можно использовать как орнамент или как рисунок для ковров.

Есть гипотеза, что длительное наблюдение за меняющимся узором Трюше способно донести до зрителя содержащуюся в потоке данных информацию. Тем более, что, по словам Шри Ауробиндо, человеческий мозг не генерирует мысли сам, а лишь транслирует их как телевизор, получая из внешнего поля неизвестной пока природы.

Два вопроса для читателей с развитым воображением. Первый – как изменится картина, если поменять местами плитки, соответствующие нулю и единице соответственно? Сохраниться ли просматриваемая «разумность» сигнала»? Второй – создадим кубики Трюше, вырезав у четырех вершин куба сферы с радиусом, равным половине ребра. Сколько вариантов модификаций кубика Трюше существуют? Получим ли мы объемный трубопровод-лабиринт с замкнутыми полостями? Или эта идея в принципе невыполнима, даже если предположить, что мы сможем рассмотреть внутренности пространства, заполненного кубиками Трюше, из четвертого измерения? Убедившись в бесплодности заполнения пространства кубиками с вырезанными сферами рассмотрим более похожую на плитки модель: в середине каждой грани кубика врезан шланг, идущий к середине смежной грани. Сколько вариантов таких кубиков может существовать? Построим ли мы ими сквозной трубопровод и как оценить количество замкнутых полостей?
Вот и все с визуализацией информации. Остаётся только решить один небольшой вопрос (а его обязательно задаст въедливый читатель, тем более, что я сам его не решил) – с каким шагом укладывать плитки, или, точнее, сколько плиток в каждом ряду? Это число полностью меняет картину, но, надеемся, не позволит спутать разумный сигнал с белым шумом. Тем более мы заранее картину не планируем и любое значение шага не более предпочтительно, чем соседнее. Был бы признателен каждому, кто предложит разумное обоснование какого-либо значения шага укладки плит.