Четыре шага к новому искусству часть 2 Опубликовано в журнале Hard'n'nSoft №12 2001 Стр. 88

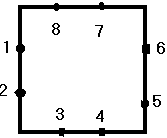
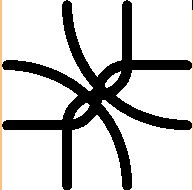
Для оптимальной загрузки статья разбита на 2 части:
Шаг первый. Плитки и шизофрения  и Шаг второй. Шестилапые и анимация смотрите здесь.
Шаг третий. В гостях у профессора Пола Брауна и Шаг четвертый. Искусство нового века читайте  на этой странице. 
Также посетите Вернисаж изображений, в том числе и Пола Брауна.

Шаг третий. В гостях у профессора Пола Брауна (www.paul-brown.com) 

Трудно передать восторг от знакомства с работами австралийского художника-математика Паула Брауна. Он доработал плитки Трюше, взяв на каждой стороне квадрата по две точки и соединяя их, соответственно, четырьмя линиями. Эта идея дает потрясающий эффект, даже сами статичные картинки вариантов красивы, а уж о движущихся на экране живых бурлящих соединениях и говорить нечего.

Сразу же вопрос - сколько вариантов соединений существует? Конечно, больше, чем мы насчитали в шестиугольнике, но в обозримых пределах, ведь здесь также, проводя одну линию, мы убираем из дальнейшего рассмотрения две точки. Я насчитал 105 вариантов соединений без учетов поворотов и отражений, если кто-то меня поправит, буду признателен. Количество уникальных вариантов с учетом поворотов-отражений, естественно, намного меньше, жду соображений читателей. Идея не отпускает, пока не напишите программу и не наиграетесь с параметрами, причем сам процесс написания, кодирования, продумывания алгоритма необычайно приятен. Задав массив, и начав его заполнять, вы столкнетесь с массой чудесных трудностей, например, если первая точка соединяется с пятой, то они обе выбывают из кандидатур для соединений с другими точками. Но, уверяю вас, затея стоит того. 

Когда на экране зашевелятся червяки, ежесекундно рождая и разрушая самые замысловатые соединения, вы почувствуете себя мини-Творцом. Невозможно не привести замечательную конструкцию, появившуюся в программе: a(a(i))=i, она красива сама по себе, не представляю, в какой еще задаче она могла бы появиться. Сразу хочется поэкспериментировать, поменять количество квадратов на плоскости, толщину линий, размер квадратов, паузу между движениями, и каждый шаг порождает по-своему замечательный процесс, который хочется сохранить. Смотреть на это "бурление червяков" не надоедает, поэтому я сделал из них скринсейвер. Еще пару слов о программе. Задав выбор цвета линий случайным образом и толщину линий в 20 пикселей, я получил невероятно красивую пестро-бурлящую абстрактную картину, насмотреться на которую невозможно. Хочется повесить ее на стену, подарить друзьям. 

Однако самое замечательное в модели Паула Брауна - это его собственная реализация движения. В отличие от рассмотренных нами движений, созданных по программе или в гиф-анимации, когда движение создавалось заменой целой плитки, Браун применил анимацию, созданную с помощью Macromedia Shockwave, в этом можно убедиться, посмотрев страничку в виде html. Этот пакет для работы с векторной графикой позволил создать необычайно красивый эффект - в квадратах пары линий обмениваются точками контакта, причем другие концы каждой линии остаются на месте, словно толстые червяки соединяются в постоянно меняющиеся цепи. Словами описать невозможно, зайдите на www.paul-brown.com/gallery/timebase/chromos.index.htm Желающие могут создать своих червяков в популярном редакторе векторной графики для веб-страниц Macromedia Flash. Предлагаю интересное задание - каким либо образом выразить вид червяков в квадрате Брауна числом. Чтобы, меняя, например разряды в двоичной записи числа, получать заранее определенный вид квадрата. А по числу однозначно построить квадрат с червяками. Мне пока не удалось. 
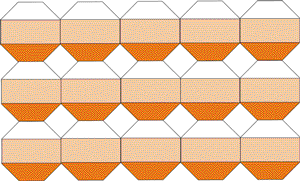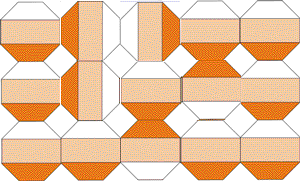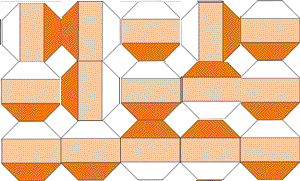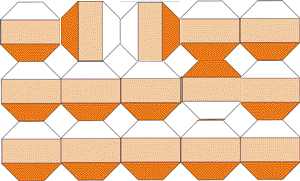
О замечательной программе, рисующей движущихся червяков, смотрите в заметке Фантастические червяки.

Шаг четвертый. Искусство нового века 

Вы заметили, что рассмотренные нами картинки красивые? Почему вообще математические картинки - фракталы, аттракторы, мозаики так красивы? Так сказочно, обворожительно, волнующе (какие еще есть эпитеты?) красивы. Так красивы, что материалисты-циники, с усмешкой отбрасывающие многочисленные брошюры, выводящие наличие Бога из красоты окружающего мира, просто в недоумении. "Когда передо мной прекрасный часовой механизм, я невольно думаю об авторе, сотворившем его" - восклицал Бенедикт Спиноза. Размышления и восторги по поводу красоты математических картинок, может, и не приведут нас в Церковь (наверное, этого недостаточно), но оставят в изумлении. Ведь если красота горных вершин, звездного неба или морского прибоя ожидаема, привычна (а как же иначе?), то откуда же берется, например, красота возводимых в квадрат комплексных чисел? Математика вся пронизана красотой и гармонией, но ведь мы сами выдумали числа, назначили правила их существования и действия над ними. В этом отношении они сродни шахматам - искусственно придуманным правилам жизни некоторых объектов. И тоже несущих в себе красоту, (помимо спортивного азарта). Как-то, разбирая партии Капабланки, я был поражен, сколько в них интриги, остроумия и изящества. (К сожалению, позже, особенно с приходом Тиграна Петросяна, красота партий шахматистов верхних эшелонов стала менее доступной для простых любителей, постоянные неочевидные попытки улучшения труднопонятных позиций, но, скорее всего, я просто слаб в шахматах.)

Для технарей, которых в принципе раздражают рассусоливания об искусстве еще один вопрос для размышлений. Создадим кубики Трюше, вырезав у четырех вершин куба сферы с радиусом, равным половине ребра. Сколько вариантов модификаций кубика Трюше существуют? Получим ли мы объемный трубопровод-лабиринт с замкнутыми полостями? Или эта идея в принципе невыполнима, даже если предположить, что мы сможем рассмотреть внутренности пространства, заполненного кубиками Трюше, из четвертого измерения? Убедившись в бесплодности заполнения пространства кубиками с вырезанными сферами рассмотрим более похожую на плитки модель: в середине каждой грани кубика врезан шланг, идущий к середине смежной грани. Сколько вариантов таких кубиков может существовать? Построим ли мы ими сквозной трубопровод и как оценить количество замкнутых полостей?

И снова вернемся к Полу Брауну. На его страничке представлено несколько невероятной красоты картинок, основанных на математических алгоритмах, в том числе и рассмотренных червяках. Можно было бы привести многочисленные исследования о связи математики и искусства, начиная с Пифагора, Аристотеля, Декарта, да Винчи и кончая бесконечными современными попытками скрестить кибернетику с живописью, музыкой, литературой. Но, помня о том, что чем шире угол обзора, тем он тупее, рекомендую лишь прочитать эссе "Шаги по камушкам в тумане" (Stepping Stones in the Mist, правда, на английском, но при сильном желании можно воспользоваться PROMPT'ом) все того же профессора Пола Брауна, расположенное на его страничке. Там же вы найдете и новую идею - замостить плоскость восьмиугольниками, раскрашенными тремя цветами и сделать гиф-анимацию с вращением восьмиугольников. Причем, сами восьмиугольники могут располагаться несколькими вариантами. 

Вращение будет порождать узоры и линии, рассыпающиеся и вновь возникающие, не позволяя оторваться от созерцания процесса. Эстетические чувства возникают при наличии ритма и движения (так вещают нам теоретики от искусства), в наших рассмотренных выше картинках присутствуют оба элемента. Правда для просмотра, нужно запускать программу, или, для гиф-картинок, открывать их в броузере или "смотрелке" картинок (все, конечно подумали об ACDSee). Можно и фон экрана сделать, включив Active Desktop и вызвав страничку с картинкой. Недавно появились сообщения о выпуске носимых картинок - в устройство, состоящее из плоского экрана и оснащенное флэш-памятью закачивается до пятисот картинок, выбираете фотку любимой кошечки и носите с собой пока не сядут батарейки. О поддержке гиф-анимации пока не говориться, но это дело времени. Так что скоро на стенах будут висеть переключающиеся плитки Трюше, вращающиеся мозаики и шевелящиеся червяки профессора Брауна. 

Причем, их движение можно будет синхронизировать с вашим самочувствием или с внешними источниками сигналов - это и будет искусством нового наступившего века. И создадим его мы.