|
|
|
|
|
|
|
|
|
Ломтик юбилейный, часть первая, с картинкамиТридцать
седьмой выпуск газеты-ломтика, 37 - Максимальное количество 5х степеней
чисел, необходимое для выражения их суммой любого числа. Количество кусков,
на которые делят круг 8 прямых линий. Шестиугольное число. Перестановочное
(с 73)простое число.
Разделителем мыслей у нас будет апплет,
найденный на потрясающей "Вентрелле"
http://www.ventrella.com Понаблюдайте за ним и поймете в чем
изюминка... На страницу Джефри Вентреллы указал активный арбузник-форумчанин
Некто (это ник такой..) - на ней такое... многое на ней заставляет вскрикивать от восторга, но
от искусственной жизни вообще "сносит крышу"... Итак, заходите на
http://www.ventrella.com/GenePool/gene_pool.html, скачиваете
GenePool3.exe (435кб)
Если выбрать для родителей одинаковые цвета, а в меню кнопки "View" в подменю "Look for a mini-drama" выбрать пункт "Love Triangle", то вы насладитесь созерцанием историй любви, оставляющей далеко позади бразильские сериалы по накалу страстей. А еще интереснее
задать партнеров противоположного цвета а из мини драм выбрать "Best
Lover" (что говорил Фрейд о страсти к подглядыванию?) -
программа сама перенесет вас в самое "интересное" действие - несколько
желтых гуманоидов создают потомство (не хочется
Программа имеет встроенный остроумный
хелп (на английском, естественно), а в нем есть список разработчиков.
Приведу его в знак благодарности за полученное удовольствие, спасибо!
Почему ломтик юбилейный? Арбузу 29 февраля исполняется 4 года, все уже в курсе - на главной странице, в Арбузном Форуме и Форуме Узнета давно висят объявления о конкурсе, итоги и подробности будут во второй части ломтика. Арбузные новости 1. Благодаря Дарье (бывшей жительнице Узбекистана, ныне россиянки), приславшей ссылки на прикольные арбузные фотки, открылся Пятый зал арбузной живописи. 2. В связи с юбилеем снова возник вопрос о целесообразности високосных годов (шутка), поэтому создан новый раздел История календаря, прошу. 3. Выложена статьи Геометрические преобразования и паркеты (из Кванта) и Замечательные последовательности (PDF) 4. Выложена мои статьи, опубликованные в Инфокоме-уз Сетевая жизнь картинок (поиск их в Сети) и Музыкальная шкатулка 5. В Зоне ПИ выложена статья Л. Завальского НОРМАЛЬНОЕ ЧИСЛО ПИ 6. Я проводил в Узнете конкурс на самый красивый сайт. Подробности и итоги конкурса смотрите на на страничке конкурса. Не удержусь - приведу фрагменты сайтов - победителей конкурса.
Там же, у Джефри Вентреллы можно скачать еще три программки, которые доставят удовольствие любителям математических картинок. Первая - это Bowman Fractal, которая рисует колышущееся причудливое фрактальное облако.
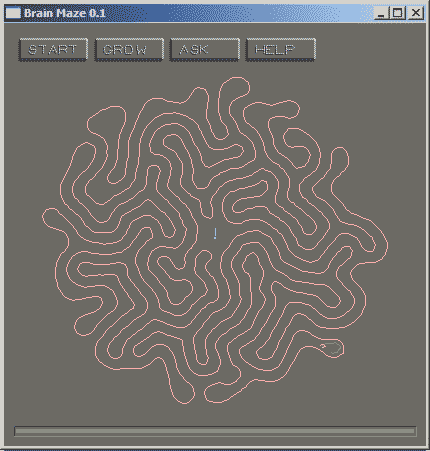
Вторя - BownMan.exe рисует замысловатый лабиринт (непостижимым образом растущий и ветвящийся) по которому можно запускать "червячка", ищущего путь к центру лабиринта.
И третья fluid.exe оставит за
курсором мышки "аттракторный"
И последнее на сегодня чудо от Вентреллы - подарок любителям многогранников. На картинке, расположенной на http://www.ventrella.com/Ideas/polyhedra.html можно проследить "родственные связи" многогранников. Ранее такие схемы мне не встречались. Для просмотра покрупнее кликните по картинке и рассмотрите - как живут додекаэдры, кубы, октаэдры и пирамиды... Эх, одно из самых-самых заветных желаний - бросить все и заняться многогранниками... Если бы я составлял заповеди (скромно так...), то главным грехом выделил бы "растворение в суете"
Еще одно замечательное открытие (подсказал в Форуме E'zy) - страничка с математическими картинками, да еще какими! Например, морфинг:
И особенно "подсолнух"
Он (подсолнух) напомнил о старой дискуссии в Форуме - "почему количество дырочек в дуршлагах всегда нечетное?" и подвигнул попытаться написать программу, выводящую точки (семечки) по спирали. Пока безуспешно - если просто в полярных координатах, то с ростом радиуса ряды редеют, еще в каждом ряду надо увеличивать количество точек... пока никакие спирали не просматриваются :( Прошу любителей попытаться...
Несколько приятных ссылок. На сайте Elitarium.Ru — Дистанционное интернет-образование есть неплохая статья "История памяти", точнее, история развития понимания человеком что такое память. Онлайн-журнал New Scientist опубликовал 9 февраля статью о переброске части стока сибирских рек в Арал. Арбуз следит за этим процессом, в статье ничего нового нет, увязывается вопрос и с политическими играми в России. Там же, как оказалось, в июле 2003 года была статья об Арале, тоже, в общем-то, ничего нового. Все, кто интересуется историей техники, хайтека, компьютеров и Сети - здесь найдут историю рождения Рунета, написанную и прокомментированную авторами процесса. Всех любителей шахмат и просто красивых картинок прошу зайти на страницу Вероники Касаткиной и насладиться открывшейся галереей ВЕСТНИК РОССИЙСКОЙ АКАДЕМИИ НАУК публикует статью Круглякова Эдуарда Павловича - академика, председателя Комиссии РАН по борьбе с лженаукой под названием "ЧЕМ УГРОЖАЕТ ОБЩЕСТВУ ЛЖЕНАУКА?" Взгляните - очень познавательно.
Статья Косинова Н. В.
ЗОЛОТЫЕ ИНВАРИАНТЫ
ГАРМОНИЧЕСКИХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ, много спорного и необычного,
взгляните.
РЕШЕНА НЕРАЗРЕШИМАЯ 16-Я ЗАДАЧА ГИЛЬБЕРТА
Из переписки.
1. Пишет Валерьян Виноградов. Здравствуйте, Евгений. Замечательный у Вас сайт. После переписки Валерьян прислал исходные коды на С и ехе-шники, можете скачать zip-архив (27кб). Спасибо!
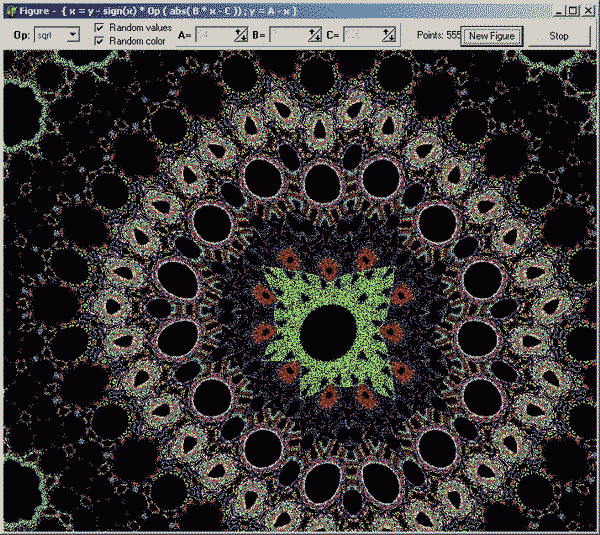
2. Пишет Вадим Потилицин Об этой формуле Б. Мартина из Астонского университета рассказано в моей статье "Волшебные точки на мониторе" (из арбузного меню статья пока не доступна), но картинки программы Вадима намного красивее моих. Например, такая: (при оптимизации gif цвета чуть померкли...)
Скачать программу можно здесь. Поиграйте с ней - просто не верится, что простейшая формула порождает такие фантастические узоры. Вот и все... |
| Автор | )c( 2000-2019 Kопирайта нет, копируйте на здоровье :) 100112 лет в Интернете |
|
 совершенно
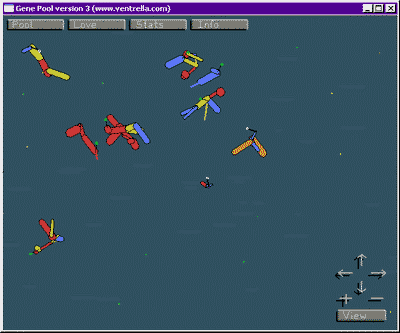
бесплатно, запускаете - и вы там навсегда... В меню Pool
выбираете один из трех типов существ
- первичный бульон со случайными конструкциями, опыты Франкештерна с чудными
монстрами и, третьи - гуманоиды. В меню Love
настраиваете параметры размножения - например, только одного цвета, - и...
наблюдаете жизнь. Организмы передвигаются, дрыгаются (чем-то напоминая
мускулами и пружинками организмы Sodaplay), и, самое
главное, они питаются разбросанными битами пищи и размножаются. Принцип
подбора партнера для воспроизводства потомства, наследование родительских
признаков плюс случайная мутация создают
совершенно
бесплатно, запускаете - и вы там навсегда... В меню Pool
выбираете один из трех типов существ
- первичный бульон со случайными конструкциями, опыты Франкештерна с чудными
монстрами и, третьи - гуманоиды. В меню Love
настраиваете параметры размножения - например, только одного цвета, - и...
наблюдаете жизнь. Организмы передвигаются, дрыгаются (чем-то напоминая
мускулами и пружинками организмы Sodaplay), и, самое
главное, они питаются разбросанными битами пищи и размножаются. Принцип
подбора партнера для воспроизводства потомства, наследование родительских
признаков плюс случайная мутация создают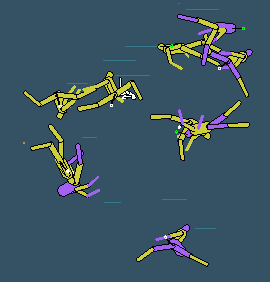 достоверную модель для проверки теории естественного отбора Чарльза Дарвина.
А наличие приятных фичей вроде масштабирования, перемещения по колонии,
перетаскивания организмов мышкой, Великой стены и пр. делают проверку еще и
чудесным развлечением.
достоверную модель для проверки теории естественного отбора Чарльза Дарвина.
А наличие приятных фичей вроде масштабирования, перемещения по колонии,
перетаскивания организмов мышкой, Великой стены и пр. делают проверку еще и
чудесным развлечением. говорить
о любви в этом контексте) с сиреневыми подругами. И вот тут стоит поглядеть
на их детишек - они пестрые, желто-сиреневые в самых разных вариантах, и их
дети пестрые и дети их детей... и по закону Менделя появляется иногда чисто
желтый или сиреневый ребенок, (а пару раз родился красный - что тут говорит
генетика?). А еще... - но нельзя же пересказывать удовольствие, которое вы
можете получить самостоятельно...
говорить
о любви в этом контексте) с сиреневыми подругами. И вот тут стоит поглядеть
на их детишек - они пестрые, желто-сиреневые в самых разных вариантах, и их
дети пестрые и дети их детей... и по закону Менделя появляется иногда чисто
желтый или сиреневый ребенок, (а пару раз родился красный - что тут говорит
генетика?). А еще... - но нельзя же пересказывать удовольствие, которое вы
можете получить самостоятельно...