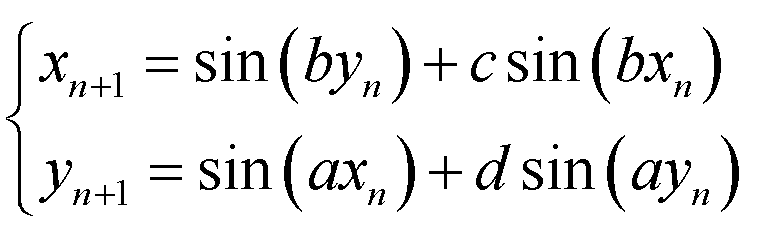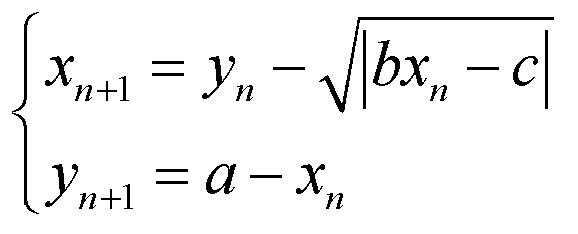Волшебные точки на мониторе

(Опубликовано в Домашнем компьютере №4 2002)

О мировой славе мечтают миллионы людей, тех
самых, которые мучительно думают, чем бы
занять себя в дождливый воскресный вечер (Доди Смит)

Люди придумали цифры и действия с ними, а потом в них же открыли множество законов, правил и теорем. Кроме того, оказалось, что в жизни цифр, линий, углов и бесконечно малых величин можно увидеть много красивого – изящные теоремы, тела, поверхности, даже условия задач. Числа живут своей жизнью, и мы, соприкоснувшись с ней, удивляемся, а иногда и любуемся ею. Компьютер дает нам возможность видеть на экране те или иные процессы, которые мы программируем. Особенно привлекательны, согласитесь, процессы, которые протекают по заданным нами правилам, но живут своей удивительной жизнью. Например, игра «Жизнь» - мы задаем "алгоритм жизни" и затем с волнением наблюдаем протекание этой самой жизни. Чем-то сродни «Жизни» и шахматы: мы сами придумали правила игры и благодаря этому получили возможность восхощаться красивыми комбинациями, изучать дебюты, возмущаться организацией чемпионатов (впрочем, это уже игры людей и больших денег). Самое удивительное, когда числа живут сами своей жизнью, а мы, наблюдая ее, пребываем в заблуждении, что управляем ими. 

Для начала рассмотрим удивительную формулу Хнов=К*Хстар*(1-Хстар). У серьезных математиков она называется «отображением Ферхюльста» и на первый взгляд ничем не примечательно – ну подумаешь, новое число последовательности зависит от старого по простейшей формуле. Но здесь таится необъяснимый сюрприз – все зависит от коэффициента К. Если мы, начав с какого-нибудь малого X, будем исследовать всю получаемую последовательность значений, то при К=1 и К=2 последовательность вырождается: график ее (по горизонтальной оси пустим счетчик цикла, по вертикальной оси – значения чисел нашей последовательности, масштаб подбирается за пару секунд) будет прямой линией. Но при приближении величины К к трем и увеличении его до четырех картина меняется – последовательность «оживает» и непредсказуемым образом «располагается» в пределах некоторого коридора! На приведенном рисунке внизу нарисован график изменения значения функции во времени, а сверху, для наглядности, прорисованы значения эти значения в осях «старое значение» - «новое значение» (как и следовало ожидать, это самая обыкновенная парабола). 

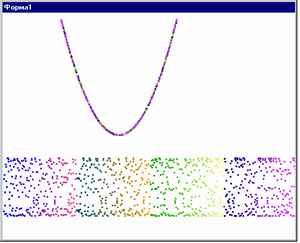
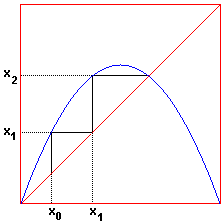
Но примечательно, что «новые» значения последовательности, становясь «старыми», тоже укладываются в эту же самую параболу. Для наглядности на рисунке цвет зависит от номера счетчика. Каждый желающий может поискать не найденные еще свойства этого чуда, запустив необычную последовательность на своем компьютере. Правда, при дальнейшем увеличении К процесс идет вразнос, вызывая «ошибку переполнения». 

Public a, x, ss, v As Integer 
Private Sub Form_Load() 
Randomize (Timer) 
ss = 2 
v = 1# 
a = 4# 
x = 0.1 
End Sub Private 
Sub Form_KeyPress(keyascii As Integer)
 If keyascii = 32 Then End 
End Sub 
Private Sub Часы1_Timer()
 v = v + 1 
x1 = a * x * (1 - x) 
red = Int(v) Mod 255 
green = (v / 3) Mod 255 
blue = Abs(255 - v / 2) 'Mod 255 
Coll = RGB(red, green, blue) 
Line (100 + x * 200, x1 * 200 + 10)-Step(ss, ss), Coll, BF ‘ Рисует параболу 
Line (v / 2, x1 * 100 + 250)-Step(ss, ss), Coll, BF ‘ Рисует график последовательности 
x = x1 
End Sub 

Интересную модель рассмотренной функции можно найти на страничке профессора математики университета Айовы Александра Богомольного (http://www.cut-the-knot/blue/chaos.html). Он пишет, что с последовательностью Хнов=К*Хстар*(1-Хстар) впервые столкнулся австралийский математик Роберт Мей изучая ежегодный прирост городского населения. С одной стороны этот прирост прямо пропорционален количеству жителей, но, с другой стороны, из-за ограниченности ресурсов, обратно пропорционален тому же количеству жителей, что и отражено в формуле. Для отслеживания процесса Богомольный предлагает построить график f(х)=k*x*(1-x) и провести линию через начало координат f(x)=x (или под 45 градусов при равенстве осевых масштабов). Выбрав любое начальное значение х, мы проводим вертикальную линию до пересечения с параболой, потом, из точки пересечения проводим горизонтальную линию до пересечения с графиком прямой линии. Так как х новой точки равен f(x) предыдущей, то мы можем повторять эту операцию многократно, отслеживая процесс графически. 

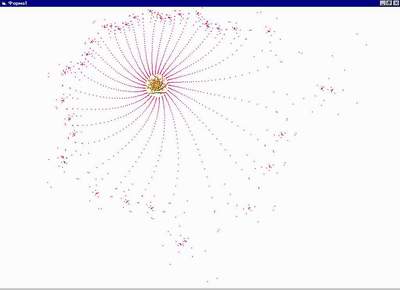
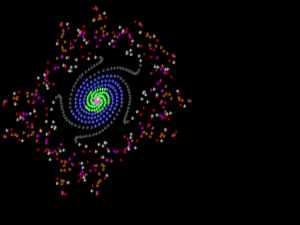
И мы увидим, как в зависимости от вида параболы (то есть, коэффициента k), проводимые нами линии или затухают, или идут вразнос, или пульсируют в некоторых пределах, отражаясь от параболы и от линии. На страничке выложен Java-аплет, позволяющий проследить все отражения выбранных вами начальных точек. 

Интересный материал об этой зависимости расположен также на http://www.ghcube.com/fractals/feigenbaum.html под названием ДЕРЕВО ФЕЙГЕНБАУМА (Добавлено после публикации)

Движемся далее. Путешествуя по дальним уголкам Сети (забавная фигура речи. А в самом деле, могут ли у Интернета быть "дальние уголки"?), я попал как-то к Мишелю, студенту университета в Виктории (Канада). Пропустив его многочисленные увлечения, в том числе расчет траекторий движения спутников и даже активное участие в «Движении геев, лесбиянок и бисексуалов», нашел замечательную вещицу. (http://www.geocities.com/WestHollywood/3101/logistic.html ) Мишель исследовал эту же формулу Zn+1 = k * Zn * (1 - Zn), но рассматривал z и k как комплексные числа, состоящие из реальной и мнимой частей. Далее Мишель приводит потрясающий рисунок, полученный из значений  Z = 0.5 + 0.1i и k = 1.1 + 0.698i 

Текста программы и подробностей реализации не приводится, у меня не получилось такого красивого фантастического облака. Но зато получилось нечто другое. На приведенном рисунке внутренний цикл вычисления Z (три тысячи раз) вложен во внешний, в котором меняется мнимая часть начального числа, что и позволяет получить закручивающиеся лучи. Желающие могут проверить правильность перемножения комплексных чисел, поменять начальные значения и получить еще более красивые рисунки.

 При увеличении масштаба можно «опуститься» в сердцевину цветка, там вас ждет тоже забавный узор. Алгоритм очень «нежный», некоторые изменения в подобранных параметрах даже в пятом знаке после запятой могут отправить процесс «в космос» (все та же ошибка переполнения), что затрудняет подбор красивых рисунков. 

Dim re1, re2, re3, re4, im1, im2, im3, im4, ix, y As Integer 
Private Sub Form_Load() 
re1 = 0.2 
im1 = 0.38 
re2 = 0.649 
For im2 = -0.8015 To 0.755 Step 0.03805 
     For i = 1 To 3000 
          re3 = re1 - re1 ^ 2 + im1 ^ 2 
          im3 = im1 - 2 * re1 * im1 
          re4 = re2 * re3 - im2 * im3
          im4 = re2 * im3 + re3 * im2 
          x = Int(re4 * 800) + 400 
          y = Int(im4 * 800) + 200 
          Line (x, y)-Step(1, 1), RGB(Abs(im2 * 300 Mod 255), 90 + im2 * 90, i Mod 255), BF 
          re1 = re4 
          im1 = im4 
          X1 = x: Y1 = y 
      Next i 
      re1 = 0 
      im1 = 0.038 
      re2 = 0.649 
Next im2 
End Sub 
Private Sub Form_KeyPress(keyascii As Integer) 
If keyascii = 32 Then End 
End Sub 

Настоящие любители могут усмотреть здесь связь с фрактальными алгоритмами (в обоих случаях многократно перемножаются комплексные числа), но есть существенное отличие – при прорисовке фрактальных картин берутся все точки плоскости и их цвет определяется вычислениями множества, а здесь все «растет» из одной начальной точки.

Путешествуя по математическим страничкам, я встречал и такой алгоритм рисования красивых фракталов: 
Xнов=А1*Х^2+А2*X+A3*Y^2+A4*Y+A5*X*Y+A6 
Yнов=B1*Х^2+B2*X+B3*Y^2+B4*Y+B5*X*Y+B6 
Приглядитесь – это как раз по теме нашего разговора, координаты новой точки зависят от координат предыдущей, да еще не просто зависят, а через квадратный многочлен, связывающий обе координаты предыдущей точки. Несколько раз брался я «поиграть» с этими штучками, предчувствуя появление волшебных картин, но, неудачно. Никак не удавалось подобрать масштаб, цвета, глубину цикла, программа затыкалась или рисовала сущие гадости. Недавно получаю очередную рассылку Интернет-зоны, с рекламой, советующей идти на Downloads портала km.ru, послушно иду, а там, в лидерах загрузки рисовалка фракталов. Я стараюсь не пропускать подобные штучки, иду к создателям, и в описании программы вижу приведенный выше алгоритм, причем картины рисует, судя по скриншотам, не хуже «настоящих», то есть, основанных на множествах Мандельброта, фракталов. Я, естественно, сажусь снова за Visual Basic и вдруг сразу получаю потрясающие картины. 

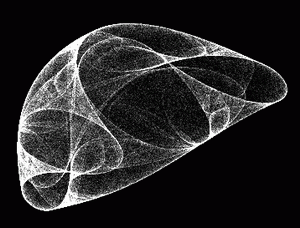
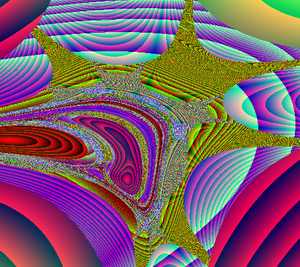
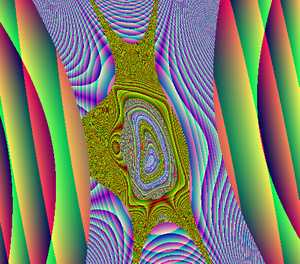
В благодарность за «толчок» приведу адрес создателей рисовалки, интересная страничка, www.yurkinsoft.chat.ru. Это не реклама, ведь не будете же вы, читатели, скачивать рисовалку фракталов с юркинсофта, это все равно, как повару-кондитеру покупать торт в кулинарии, весь смысл-то попробовать самим. Тем более, что приведу текст отлаженной программы. 

Public h, scal, ss, xx, yy, j, red, blue, green As Integer 
Dim a(10) As Single, b(10) As Single, k As Integer, _ x As Single, y As Single, y1 As Single, x1 As Single 
Private Sub Form_Load() 
Randomize (Timer) 
h = 500 ‘ сторона квадратной картинки в пикселях 
k = 400 ‘ максимальное значение количества итераций 
ss = 1 ‘шаг рисования 
scal = 50 ‘ масштаб 
End Sub Private 
Sub Form_KeyPress(keyascii As Integer) 
    If keyascii = 32 Then End 
End Sub 
Private Sub Часы1_Timer()
Cls 
For i = 1 To 6 
   a(i) = Rnd * 3 - 1 
   b(i) = Rnd * 3 - 1 
  Print i; "a="; a(i); "b="; b(i) 
  Next i 
  For xx = 1 To h Step ss
    For yy = 1 To h Step ss 
       x = (xx - h / 2) / scal 
       y = (yy - h / 2) / scal 
      For j = 1 To k 
         x1 = a(1) * x ^ 2 + a(2) * x + a(3) * y ^ 2 + a(4) * y + a(5) * x * y + a(6) 
         y1 = b(1) * x ^ 2 + b(2) * x + b(3) * y ^ 2 + b(4) * y + b(5) * x * y + b(6) 
         If Abs((x1) + (y1)) > 20 Then Exit For ‘Выход по условию из цикла 
         x = x1 
        y = y1 
      Next j 
      red = Abs(Int(x1 * 20)) Mod 255 
      blue = Abs(Int(y1 * 10)) Mod 255 
      green = (j * 88) Mod 255 
      Line (xx + 200, yy + 5)-Step(ss, ss), RGB(red, blue, green), BF 
  Next yy, xx 
End Sub 

Не забудьте «кинуть» таймер на форму, дав ему минимальную паузу, выбрать Scale mode в пикселях и прочие мелочи. Программа без остановки рисует фрактальные картины, для которых все шесть коэффициентов каждый раз выбираются случайным образом. Придирчивые ценители фрактальных картинок заметят, что красный цвет зависит от координаты X, а зеленый - от координаты Y последней точки итерационного цикла, и только синий цвет зависит от номера счетсика. Такой прием позволяет "раскрасить" картину и дает простор для экспериментов.

Еще один аттрактор (так называются на математических страничках в Сети эти чудные непредсказуемые изображения из точек) выложен в виде Java-аплета на http://www.mathpuzzle.com/applets.html. Нас же интересует его алгоритм, довольно незатейливый и просящийся на экран. 

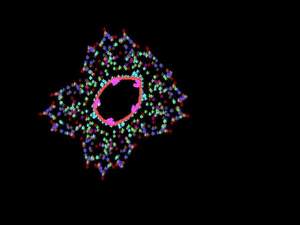
Удивление от формы появляющихся дымчатых картин с лихвой компенсирует все наши хлопоты с выбором масштаба и отысканием подходящих коэффициентов. Вот некоторые аттракторы. 

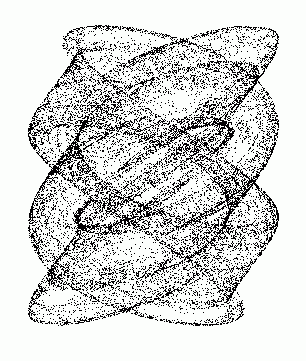
И, наконец, рассказывая о красивых «точечных» процессах на экране, невозможно не вспомнить знакомую многим любителям компьютерных развлечений замечательную формулу, придуманную Б.Мартином их Астонского университета: 

Посмотрите, как оригинально новые значения X и Y связаны со старыми: новый X зависит от старого Y, а новый Y – от старого X, причём, чтобы процесс не пошёл "вразнос", при вычислении X от старого Y отнимается X^1/2. А для того, чтобы ситуация нами (якобы) контролировалась, введены коэффициенты A, B и C. Сразу же возникает желание посмотреть, как же уложатся точки, если их координаты менять по приведённой формуле. И желание не напрасное, так как результат необычайно красив. Предлагаю текст программы на Паскале, которая позволит вам поиграть с формулой и полюбоваться её жизнью на экране. Программа выбирает точку с координатами (100,100), что не существенно, можно начать с любой точки. Потом запрашиваются три числа (целых), это и есть коэффициенты A, B и C. Для выхода из программы надо ввести А=0. Потом запускается цикл из 1000 шагов преобразований координат по формуле, на каждом шаге в соответствующе точке выводится символ “*” цветом, меняющимся через каждые 100 шагов. В строке 4 добавлены константы для расположения узоров в центре экрана. 

PROGRAM uzor; 
USES GRAPH,DOS,CRT; 
VAR GraphDriver : Integer; { для графического адаптера } 
GraphMode : Integer; { для графического режима } 
ErrorCode : Integer; { для кода ошибки } 
I,X,X1,Y,a,b,c : INTEGER; 
BEGIN 
GraphDriver:= Detect; { режим автоопределения } 
InitGraph(GraphDriver,GraphMode,''); { инициализация} 
settextstyle(1,0,1) ; 
repeat 
    gotoxy(1,1) ; 
    x:=100 ; y:=100 ; {1} 
    read(a); if a=0 then exit; read(b,c); 
    SETFILLSTYLE(1,0) ; BAR(0,0,640,480); 
    for i:=1 to 1000 do begin 
        x1:=x ; x:=trunc(y-sqrt(abs(b*x1-c)))-100; {2} 
        y:=a-x1; 
        setcolor(trunc(i/100)+4); {3} 
        outtextxy(x+300,y+100,'*'); {4} 
   end; 
UNTIL KEYPRESSED; 
END. 

Запустив программу и введя наугад три числа 55, 66 и 77, сразу получим узор, напоминающий цветок.

>Введя числа 111,11,1 получим гиперболы. Числа 1,1,1000 дадут спираль, а 11,111,1 – замысловатый узор. Особенно интересно наблюдать изменения формы узора, меняя одно из трёх чисел, оставляя два без изменения. Можно добиться, чтобы узор рассыпался в звёздное небо или, наоборот, выродился в несколько точек. Попробуйте, поэкспериментируйте, и вы еще раз убедитесь в том, что числа живут своей собственной жизнью, а мы самонадеянно уверены, что управляем ими.