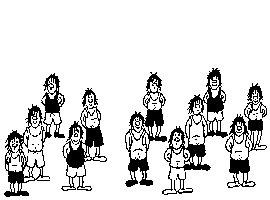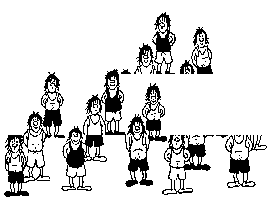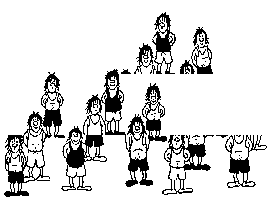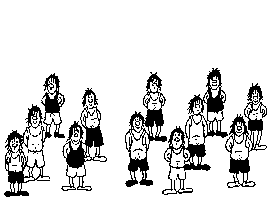Ломтик обезьяний
Первый выпуск в 2004 году, отсюда и название. Тридцать
шестой выпуск газеты-ломтика, 36 - наименьшее (кроме1) одновременно и
квадратное и треугольное число. Подробнее о треугольных числах смотрите
статью о треугольнике Паскаля. Кто знает еще интересные свойства
номеров газет - сообщайте в Форум или мылом. С числом 36 связано много
задач, вот самая красивая из них. Один математик, будучи в гостях у
сослуживца, спросил, сколько лет его детям. Хозяин ответил, что произведение
возрастов его трех детей равно 36. Гость казал, что этого мало, тогда хозяин
сообщил сумму возрастов детей. Гость опять сказал, что этого недостаточно. И
лишь после того, как хозяин сообщил, что старший ребенок - мальчик, гость
смог назвать возраст каждого ребенка... А вы?
Начнем, как всегда, с картинки

Картина найдена в
галерее
Вольфрам-ком, домашней страницы специального пакета математических программ.
И еще одна картинка из этой же галереи

Рассмотрите ее. Это те самые шестиугольники, которые
описаны в статье "Четыре шага к новому искусству"
в главе "Шестилапые и анимация". От ориентации плитки зависит вид кривой
линии - она или идет от края до края, или замыкается самым причудливым
образом. Поиграйте с такими шестиугольниками, очень рекомендую. А если кто
сделает флэш- или гиф-анимацию, будет просто здорово!

напоминаю - разделитель тем еще и
ссылка на Форум для обсуждения ломтика
Интересный материал - дополнение к статье Константина
Кнопа в Арбузниках Мир тесен
|
Мир не так уж тесен
Авторитетный научный журнал Science в последнем номере сообщил
об итогах эксперимента, известного под названием Six Degrees of
Separation ("Шесть степеней удаленности" или "Шесть рукопожатий" -
в последнем случае предполагается, что каждого человека на планете
с другим человеком связывает цепочка из шести знакомых).
Напомним, что гипотеза о шести степенях удаленности
была высказана психологом Стэнли Милграмом (Stanley Milgram) в
1967 г. То, что нужно именно 6, а не 5 или 7 степеней удаленности
для передачи личной информации, Милграм установил в результате
эксперимента, в ходе которого жителям небольшого провинциального
городка Омаха в штате Небраска было роздано 300 конвертов. Эти
конверты необходимо было передать определенному человеку,
проживающему в Бостоне, штат Массачусетс, причем конверты надо
было передавать только через своих родственников и знакомых. Всего
до адресата дошло 60 из 300 конвертов. Милграм в итоге установил,
что в среднем каждый дошедший по адресу конверт прошел через шесть
человек.
В результате эксперимента, который имел все же ограниченную
географию и число участников, возникло предположение, что не
только в Соединенных Штатах, но и во всем мире люди, несмотря на
национальные и культурные различия, связаны теснее, чем принято
было думать раньше. Как ни странно, до последнего времени лишь
немногие исследователи пытались воспроизвести эксперимент Милграма,
который не раз подвергался в научной среде критике за
неубедительность доказательств, недостаточное число участников и
другие методические недостатки.
Появление интернета и широкое распространение электронной почты
дало возможность расширить рамки эксперимента. Сама проблема имеет
два аспекта - математический, связанный со структурой сети, и
психологический, касающийся в основном мотивации к участию в этом
эксперименте. Соответственно, и результаты исследования
представляют наибольший интерес для специалистов по компьютерным
сетям, которым будет интересна картина перемещения информация в
интернете, и психологам, изучающим тенденции распространения
слухов, а также различных культурных влияний. В ходе нового
интернет-исследования были привлечены 60 тыс. пользователей,
которые должны были передать информацию 18 адресатам из 13 разных
стран. Среди адресатов были такие разные люди, как профессор
Корнельского университета, ветеринар из Норвегии, полицейский из
Австралии. Полученный результат значительно отличался от того, что
получил в свое время доктор Милграм, - из 24613 цепочек
электронных писем лишь 384, т.е. менее 2%, достигли конечной цели.
Интересно отметить, что почти все успешные попытки оказались
короче 6 ступеней (в среднем 4). Неудачные же цепочки прерывались
в основном из-за того, что кто-то не желал отправлять письмо
дальше, т.е. не проявлял желания участвовать в этом эксперименте.
Конечно, многие получатели воспринимали письмо как спам, но все же
неожиданно высокая доля - 37% всех участников - пересылали письмо
дальше.
Результаты эксперимента поставили новые вопросы перед
исследователями. Например, выяснилось, что могло быть удачным
гораздо большее число цепочек, особенно в случае, когда первый
отправитель и адресат живут в одной стране (достаточно в среднем
пяти ступеней). Другой интересный результат - около половины
удачных "соединений" пришлось на профессора университета, хотя его
круг общения вовсе не в 10 раз шире, чем у других адресатов. И,
как ни странно, большую роль в успешной доставке электронных писем
сыграли простые случайности.
По-видимому, итоги эксперимента по проверке утверждения "мир
тесен" еще долго будут обсуждаться научной общественностью. В
Колумбийском университете уже начата подготовка к новому
эксперименту, в котором будут выясняться психологические аспекты
принятия решения о том, кому именно направить письмо. Кроме того,
у отправителей появится возможность направить письмо не одному, а
нескольким адресатам.
Источник: по материалам газеты
The New York Times.
Адрес статьи: http://www.cnews.ru/newtop/index.shtml?2003/08/12/147328
|
.
|
Биквадратные числа - это ряд n4 - 1,
16, 81, 256, 625,1296, 2401, 4096, ...
Минимальное количество биквадратных чисел (складываемых
или вычитаемых), необходимых для представления чисел 1, 2,
3, ... равно 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11,
12, 13, 14, 15, 1, 2, 3, 4, 5, ...
Подробнее об этом
здесь - рассмотрите и другие последовательности... |

Арбузные новости...
Главная новость - изменилось оформление. Прошу обсудить
в Форуме.
В музее Зоны ПИ открыт второй зал.
Прошу.

На странице "Искусственный
Интеллект в домашних условиях", в разделе астрономии, есть
интересная
статья с новой формулой закона Всемирного тяготения. Для нас интересна
тем, что теперь в формуле участвует число Пи. :)

Кушнер Александр
Анекдот. Открывается дверь,
Входит смерть, вот такого росточка.
Очень острую держит, поверь,
Косу, вся - не крупней ноготочка
Твоего. В капюшончике. Что ж,
Умереть? Я готов: от злодейки
Все равно никуда не уйдешь.
- Извини, я к твоей канарейке.

Отличная задача от одного из самых
популярных жж-стов Анатолия
Воробьева. Ломтики около года назад цитировали его, если помните заметку
"Гравитация утонула".
|
об обедающих криптографах
Прочитал об алгоритме обедающих криптографов. Понравилось — остроумно!
Перескажу.
Предположим, трое криптографов пришли в какой-то ресторан пообедать.
После того, как они уселись за стол, официант сообщает им, что их обед
оплатил заранее некий анонимный доброжелатель.
Криптографы знают, что этим доброжелателем мог быть один из них, но,
кроме того, им мог быть некий внешний орган (определённости ради
предположим, что этим внешним органом может быть только NSA, федеральное агентство национальной безопасности США, очень
интересующееся криптографией и криптографами). Они хотят выяснить,
действительно ли заплатил за обед один из них, или это дело рук
NSA . Но при этом они очень тактичны, так что,
если заплатил один из них, они не хотят, чтобы другие двое об этом
узнали. Поэтому они не могут, скажем, просто договориться, что тот из
них, кто заплатил (если есть такой), признается в этом.
Могут ли они выяснить, заплатил ли один из них, не выдавая при этом
самим себе информацию о том, кто именно? Оказывается, могут, и вот как.
Каждый из них кидает монетку и показывает результат (орёл или решка)
своему соседу справа. Таким образом есть три броска монетки, и каждый
криптограф знает результат двух из них (той, что он сам бросил, и той,
что бросил его сосед слева и показал ему результат). Далее, каждый из
них говорит вслух следующую информацию: одинаковые два результата он
видел, или разные (например, если у него вышел орёл, а у соседа слева
решка, он говорит "разные"; если у него решка, и у соседа слева решка,
говорит "одинаковые", итп.) — но с одним исключением: тот из них,
который заплатил за обед (если есть такой) говорит наоборот, т.е.
если он видит два разных результата, говорит "одинаковые", если видит
два одинаковых, говорит "разные".
Простое задание: докажите, что этот алгоритм позволяет им определить,
заплатил ли кто-то из них за обед, но вместе с тем не позволяет им (тем,
кто не платил) узнать, кто именно. Это несложно и занимательно. Для тех,
у кого не получается или лень думать, объяснение:
Если все трое говорят правду, т.е. никто из них не платил за обед, то
количество ответов "одинаковые" обязательно будет нечётным (например, 3,
если у всех выпала решка, или 1, если выпал один орёл и две решки, итд.).
Если же один из них заплатил, то он говорит наоборот, и это меняет
количество ответов "одинаковые" на единичку, поэтому их теперь будет
чётное число. Таким образом, чётное число ответов "одинаковые"
прозвучало, или нечётное, позволяет определить, платил за обед кто-то из
них, или NSA .
Теперь о том, почему это не даёт им никакой новой информации о том, кто
заплатил за обед. Если за обед заплатило NSA , то
понятно, что они узнали об этом и всё. Если за обед заплатил один из них,
то сам он об этом знает, остаётся доказать, что не знают двое других.
Предположим, я — один из тех, кто не заплатил. Есть два варианта: либо я
видел два одинаковых результата, либо два разных.
Предположим, я видел два одинаковых результата, скажем, два орла. Т.к.
число ответов "одинаковые" было чётным, ещё один криптограф, кроме меня,
ответил "одинаковые", а третий ответил "разные". Я не знаю результата
той монетки, которую видели второй и третий. Если она выпала орлом, то
второй говорил правду, а третий врал, и значит, он оплатил обед; если
решкой, то второй врал, а третий говорил правду, значит, второй заплатил
за обед. Но т.к. результат падения монетки был случайным, у меня нет
никакой информации, позволяющей выбрать между этими двумя исходами — я
знаю не больше, чем раньше, о том, кто из них мог заплатить.
Совершенно симметричный этому аргумент проходит в том случае, когда я
видел два разных результата.
По-моему, очень красиво. Этот алгоритм придумал David
Chaum и опубликовал в 1988-м году в статье
The Dining Cryptographers Problem: Unconditional
Sender and Recipient Untraceability , которая есть в сети (см.
ссылку). |

О квадратах, головоломках и правополушарном
мышлении говорили в Арбузном Форуме с подачи Сергея Ф. А
началось все с поста:
|
"Можно ли из
попарно различных квадратов собрать какой-либо прямоугольник?" Эта
головоломка достаточно долго занимала умы математиков в первой половине
XX века. В 1925 году польскому математику З. Морону удалось решить эту
проблему: он показал, что из девяти попарно различных квадратов со
сторонами 1, 4, 7, 8, 9, 10, 14, 15 и 18 можно сложить прямоугольник.
Материалы по этой проблематике содержатся по адресу:
http://www.px-pict.com/5/2.html
Мною была разработана игра по сборке “композиции Морона”:
http://www.px-pict.com/5/2/3.html
В этой игре квадраты уже присутствуют на экране и вам нужно только лишь
передвинуть их мышью, чтобы из них сложился прямоугольник.
Интересно отметить, что, занимаясь решением этих головоломок, математики
открыли связь между прямоугольниками, собранными из квадратов, и
электрическими сетями. А именно: выяснилось, что такие прямоугольники
могут рассматриваться как "коды" вполне определенных графов и
электрических сетей. См. по этому поводу:
http://www.px-pict.com/5/3.html
|

Эти скульптуры сделаны из снега.
Отсюда.





Постоянный участник Арбузного Форума
E'zy выложил в форуме замечательную картинку -
присмотритесь, на ней то 12, то 13 человек. Куда один пропадает и откуда
появляется?
Истинные любители головоломок помнят подобные
картинки в книгах М. Гарднера - там при повороте части картинки тоже
пропадал или появлялся человек. Кто объяснит? :)

Если Вы думаете, что только на Арбузе
"копирайта нет, используйте любую информацию в своих целях", то напрасно.
Автор "Академии виртуального общения
Красные глаза" Николай обратил мое внимание на
"копирайт" Андрея Матюшкина:
Все, что покоится в недрах этого сайта может быть
использовано в любых целях, включая: модифицирование с целью улучшения,
купирование с целью ухудшения, цезурирование с целью сокращения, цитирование
с целью прославления и даже модерирование с целью глумления. Вы можете
продавать, покупать, дарить и красть все написанное мною. Любое
стихотворение и байка с этого сайта могут быть выданы за свои. В случае
письменного уведомления автора сайта о намерении отсюда что-нибудь слямзить,
я обещаю единожды подтвердить Ваше авторство любой из написанных мною вещей.
Этот тип лицензии носит характер эзотерической прострации.

Вот и все... |