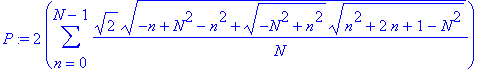p-Club или Клуб фанатиков числа p

Зал №2    Перейти в Зал №1

Зал №2 содержит дополнения, появившиеся после создания зала №1.

Прежде всего - сообщение о невероятном скрипте. Вот фрагмент из Форума
найденного здесь

И еще о том же скрипте из другого блога:

Я тоже пытался открыть эту страницу - полезли колонки цифр, вертикальный скроллбар быстро уменьшался, через несколько секунд я снял задание, испугался, что большой файл подвесит IE и локальную сеть. Но, имейте в виду, что такая штука есть.

Новость, прошагавшая по всем популярным сайтам - о том, что цифры числа Пи олицетворяют хаос. Например, сообщение с Компьютерры+

[08.08 12:00] Дело случая.

Последовательность цифр в числе Пи, издавна волнующая умы математиков своей непредсказуемостью, действительно случайна.
На сегодняшний день число Пи известно с точностью до 500 млрд. знаков, в которых так и не найдены какие-либо повторения. И, если верить работе американского физика Дэвида Бейли и канадских математиков Питера Борвина и Саймона Плофе (David Bailey, Peter Borewin, Simon Plouffe), таких повторений найдено никогда и не будет. Доказали они это просто: составили компьютерную программу, которая вычисляет любой знак в числе Пи почти ничего не зная... о знаках предыдущих. Достижение, считавшееся до сих пор невозможным (Пи представляет собой отношение длины окружности к ее диаметру и допускает вычисление себя со сколь угодно большой точностью — но начать все же нужно с самого первого знака после запятой), стало реальностью благодаря применению теории хаоса: в ней существует предположение, что в нормальных числах одни числовые последовательности неким образом зависят от соседних с ними чисел (т. н. Гипотеза А).
В свою очередь, нормальными числовыми последовательностями математики называют такие последовательности, в которых числа одинаковой длины встречаются одинаковое число раз (к примеру, 123 встречается столько же раз, сколько 234 — т. е. последовательность чисел случайна). В Пи — судя по анализу вычисленных знаков — это правило соблюдается. Однако строго доказать, что Пи — нормальное число, никто пока не сумел. Это сделали вышеназванные трое исследователей, показав, что числа в Пи подчиняются теории хаоса, а значит, случайны.
По словам математиков, доказательство того, что Пи — случайно и никогда не повторяет самое себя, нужно отнюдь не как очередной забавный математический курьез: это важное научное достижение, на котором могут быть основаны такие чисто практические вещи, как, к примеру, создание невзламываемых шифров.

И сообщение о той же гипотезе словами Известия-Наука http://www.inauka.ru/news/01-09-02/article28705

МАТЕМАТИКИ РАСКРЫЛИ ТАЙНУ ЧИСЛА "ПИ"

Математики сделали важный шаг к ответу на вопрос, насколько случайны число "пи" и прочие математические константы. Впервые им удалось связать теорию чисел с теорией хаоса. Значение числа "пи" известно с точностью до 500 миллиардов знаков, его первые цифры - 3.1415926535. В нем нет ни одной циклической последовательности и, если математики не ошибаются, никогда не будет, сколько бы еще знаков ни вычислили.

Число "пи" - отношение длины окружности к диаметру - тысячи лет считалось мистическим, древние греки даже построили на нем религию. Любая последовательность цифр одинаковой длины встречается в нем с одинаковой частотой. Например, вероятность найти последовательность 234 равна вероятности обнаружить 876; а 23568 попадается так же часто, как 98427. Математики называют такие числа "нормальными". Другие примеры "нормальных" чисел - корень квадратный из 2 и натуральный логарифм 2. Но до сих пор строгого доказательства нормальности числа "пи" не было. Видимо, математики устали от бесплодных попыток найти это доказательство.

Как считает Дэвид Бэйли из Национальной лаборатории Лоуренс Беркли в США, нормальность некоторых математических констант связана с гипотезами из области хаотической динамики. Одна из них, так называемая "гипотеза А", утверждает, что последовательность чисел определенного вида "пляшет" между двумя другими числами. Бэйли и его канадские коллеги - математики Питер Борвин и Саймон Плуфф написали компьютерную программу, вычисляющую произвольную цифру числа "пи", не вычисляя предыдущие, - раньше это считалось невозможным.

Отличительная особенность алгоритма - то, что он работает не целиком с числом, а с его фрагментами. То есть ученые взяли числа 0.314; 0.141; 0.415; 0.159 и т.д. Все они составлены из трех последовательных цифр числа "пи". Если цифры "пи" случайны, то все эти числа должны быть случайно распределены между 0 и 1. Правда, ученые работали не с десятичной, а с двоичной записью числа "пи", то есть с последовательностями из нулей и единиц.

Вычисления по созданной Бэйли и его коллегами программе показали, что цифры числа "пи" ведут себя в соответствии с теорией хаоса, то есть, по-видимому, их последовательность действительно случайна. Возможные применения этих результатов - новый алгоритм генератора случайных чисел и криптография.

Ольга ЯКОВЛЕВА

Очень популярна в Интернете (судя по количеству копирований на разных сайтах) статья Косинова Н. В. "СВЯЗЬ ТРЕХ ВАЖНЕЙШИХ КОНСТАНТ: постоянной тонкой структуры (альфа), числа пи (p) и золотой пропорции (f=1,618…)".
Выявлена связь постоянной тонкой структуры (альфа) с важнейшими математическими константами: числом пи (p) и золотой пропорцией (f), вытекающей из последовательностей чисел Фибоначчи и Люка. Получено соотношение, связывающее эти безразмерные константы. Формула имеет вид:

альфа²⁰ =(p*f¹⁴ )^1/13·10^-43

На основе этой формулы получено новое расчетное значение постоянной тонкой структуры (альфа):

альфа == 1/137,036009823754683675307501201348…

Полученные результаты подтверждают геометрический статус постоянной тонкой структуры, а также указывают на то, что основные безразмерные параметры, которые характеризуют микромир и Вселенную определяются числами пи, альфа и золотой пропорцией  и являются принципиально вычисляемыми.

Это порождает надежду на то, что наконец-то появится хоть какая-то возможность подступиться к решению запутанной головоломки о таинственном числе “альфа”, что не дает покоя физикам. Эта константа была введена в физику Зоммерфельдом в 1916 году при создании теории тонкой структуры энергии атома. Первоначально постоянная тонкой структуры (альфа) была определена как отношение скорости электрона на низшей боровской орбите к скорости света. С развитием квантовой теории стало понятно, что такое упрощенное представление не объясняет ее истинный смысл. До сих пор природа происхождения этой константы и ее физический смысл не раскрыты. Кроме тонкой структуры энергии атома эта константа проявляется в следующей комбинации фундаментальных физических констант: альфа = (мю)₀ce²/2h. По поводу того, что константа (альфа) появляется в соотношении, связывающем постоянную Планка, заряд и скорость света Дирак писал: "неизвестно почему это выражение имеет именно такое, а не иное значение. Физики выдвигали по этому поводу различные идеи, однако общепринятого объяснения до сих пор нет". Аналогичное высказывание о числе (альфа) принадлежит Фейнману: "с тех пор как оно было открыто... оно было загадкой. Всех искушенных физиков-теоретиков это число ставило в тупик и тем самым вызывало беспокойство. Непосредственно вам хотелось бы знать, откуда эта постоянная связи появилась: связана ли она с числом пи или может быть она связана с натуральными логарифмами? Никто не знает". Относительно значения постоянной тонкой структуры авторы Берклеевского курса физики пишут: "мы не располагаем теорией, которая предсказывала бы величину этой постоянной".

По мнению автора формулы теперь можно установить геометрический, или пространственный смысл постоянной тонкой структуры, что, в вою очередь, позволит приоткрыть тайны микромира и устройства материи. Заинтересовавшихся отсылаю к первоисточнику.

Вычисление с нужной точностью числа Пи

Kantor Ilia
e-mail: algolist@manual.ru

Метод Монте-Карло

Самый простой и легкий в реализации метод.
Рассмотрим произвольный квадрат с центром в начале координат и вписанный в него круг. Будем рассматривать только первую координатную четверть. В ней будет находиться четверть круга и четверть квадрата. Обозначим радиус круга r, тогда четверть квадрата тоже будет квадратом(очевидно) со стороной r.

Будем случайным образом выбирать точки в этом квадрате и считать количество точек, попавших в четверть круга. Благодаря теории вероятности мы знаем, что отношение попаданий в четверть круга к попаданиям 'в молоко' равно отношению площадей - пи/4. Вот, собственно, и весь алгоритм... Чем больше взятых наугад точек мы проверим, тем точнее будет отношение площадей.

Вот простенькая программа на Паскале, считающая пи этим способом... Четыре первых знака требуют на моем PentiumII-300 около 5 минут...

uses Crt;
const
 n=10000000;
 r=46340;
 r2=46340*46340;
var
 i,pass : LongInt;
 x,y : real;
{$F+}
begin
 WriteLn('Поехали!');
 Randomize;
 pass:=0;
 for i:=1 to n do
  begin
   x:=Random(r+1);
   y:=Random(r+1);
   if ( x*x+y*y < r2 ) then INC(pass);
  end;
 TextColor(GREEN);
 WriteLn('Число ПИ получилось равным: ',(pass/i*4):0:5);
 ReadLn;
end.

Продолжая читать эту интересную статью, расположенную на http://algolist.manual.ru/maths/count_fast/pi.php, вы узнаете, как посчитать ПИ с помощью рядов. Эти алгоритмы мы рассматривали в статьях, лежащих в Зоне ПИ.

Повторим новость, прошагавшую в декабре 2002 года по всем новостным сайтам (скопировано с Газеты.Ru http://www.gazeta.ru/2002/12/06/kz_m70818.shtm )

Ученые Токийского университета сумели поставить новый мировой рекорд в вычислениях «числа Пи». Известную математическую константу они сосчитали до 12411-триллионного знака. Для этого группе программистов и математиков, которую возглавлял профессор Ясумаса Канада, понадобилась специальная программа, суперкомпьютер и 400 часов машинного времени, сообщает Associated Press.

Новый рекорд будет внесен в Книгу рекордов Гиннеса. Прежне рекордное достижение было поставлено учеными Канады, которые смогли сосчитать «число Пи» с точностью 206158 миллиардов знаков после запятой. Очевидно, что японцы смогли пересчитать «число Пи» в 60,2014 раза точнее.

Наиболее сложным этапом в установлении нового рекорда стала компьютерная программа, которая выполняет операцию вычисления «числа Пи», – на ее написание и отладку ушло более 5 лет. Само же вычисление отняло менее месяца и преследовало к тому же сугубо практическую цель протестировать новый суперкомпьютер Hitachi, способный выполнять два триллиона операций в секунду.

Прочтите цитату из книги, найденной на http://www.om3.org/russian/book1/Section2/2_1.htm и постарайтесь представить - о чем же идет речь:

Пространство Жизни может быть только трехмерным. Взаимодействие трех составляющих Бога (Бытиё, Небытиё, Сознание) охватывает абсолютно все процессы Природы! Способность Сознания охватить процессы Бытия и Небытия определяет мерность (диапазон) Сознания и мерность того мира, в котором живет человек. Мерность Сознания определяет возможность реализации проявленных человеком способностей в плане управления процессами Жизни.

Зарождение органической Жизни и ее существование возможны только в мерности равной числу “пи”, то есть в трехмерном пространстве. Это значит, что пространство, в котором материализуется Сущее и существует органическая Жизнь, может быть только трехмерным.Разница семи уровней Бытия определяется лишь диапазоном (мерностью) Сознания и связанными с ним Мыслительными (психическими) процессами людей, живущих на том или ином уровне. Раскрытие диапазона Сознания на 2 - 5 % не является свидетельством нашей никчемности или ограниченности, это – стандарт нашего материального мира, наш стартовый капитал!

Смысл Эволюции (на нашем уровне и на любом другом) – способность человека выйти за пределы стандарта (комфортной зоны) своего мира. Он должен найти в себе силы и мужество, чтобы выйти за пределы “нормы”, принятой общественным мнением, неписаными законами в среде ему подобных, не побоявшись стать непохожим на них или смешным. Найти силы и мужество, чтобы выделиться из этой среды. (Пойти туда - не знаю куда, найти то - не знаю что). Испытание не для слабонервных! И так на каждой ступеньке, на каждом уровне бесконечного “Пути Дао”.

Число “пи” - это не есть универсальная постоянная. Ее значение приближено к числу “3”, но не равно точно трем. За счет этого приближения к трем (отклонения, несовпадения), и создаются разные уровни Мироздания.

Если органическая жизнь зарождается при значении “пи”, приблизительно равном числу 3, то уровень возникновения Сознания в нашем мире, на Земле определяется “пи”+ 0,1 (то есть при значении “пи”= 3,1). Наличие мерности Земли в пределах 3,00017 говорит о том, что Человечество до обретения Сознания, мягко говоря, не дотягивает.Надо помнить, что проявление Бытия не ограничивается данным диапазоном. Он является стартом, отправной точкой для непрерывного расширения Сознания, для образования различных уровней существования органической Жизни во Вселенной. Каждому уровню соответствует свой диапазон Сознания. Отсюда изменяется, растет мерность пространства.

Например, в Мире Бога мерность пространства и Сознания составляет от 4 до 4,5. Мерность Сознания самого Бога составляет около 5,5 единиц, и она не стоит на месте, поскольку Эволюция не дает засиживаться и Ему. Растет Его мерность, возрастает мерность всей Его (и нашей тоже) Вселенной, а значит, и все ее население обязано повышать свою мерность, шагать в ногу с Богом!

Без комментариев - число Пи принадлежит в равной мере всем желающим го использовать....

На странице Елецкого Государственного Университета имени И. А. Бунина http://www.elsu.ru/edu/pi100000.html выложены 100 000 знаков числа Пи. Вот пример всем - чем должны заниматься университеты! :) Здесь копировать не будем, так как эта страница весит 165 кб, хотя приятно было бы лишний раз поглазеть на таинственные цифры волшебного числа.

Сколько было рассуждений о том, что в числе Пи закодирована любая выбранная нами книга, в том числе и Ветхий Завет... и вдруг узнаем, что в Торе присутствует число Пи с точностью до пятого (!!!) знака после запятой. Подробности в стате "Тора и число Пи", лежащей на http://ariel.h1.ru/articles/tnpi/tnpi_rus.html Цитата для ленивых:

Различие в написании и прочтении, записаное масоретами, подчеркнуто красной линией. Обрати внимание, здесь уже есть огласовки (система точек и других значков под словом). Надпись гласит:«пишется вэ-кав’э, читается вэ-кав», ну это еще не «30/10 пишется, а читается Пи», но уже близко.

Раньше в славянских языках буквы использовались в качестве цифр. В иврите буквы используют как цифры и числа и по сегодняшний день, паралельно с привычной нам арабской символикой. Более того, часто подсчет числового значения слов используется при исследовании Торы, это - так называемая гематрия. Числовое значение слова "кав" = (коф: 100 + вав: 6) = 106,  "кав’э" = (коф: 100+вав: 6+hей: 5) = 111. Для получения поправочного коэффициента из различий в написании и произношении, которое было сохранено для нас чрез тысячилетия, делим 111 на 106.

Умножаем наш «грубый» показатель 3 = (30/10) соотношения числа локтей на поправку: 3*(111/106) = 3,14159…
Подробности смотрите на первоисточнике...

Статья Герасима Андреева "Фи-треугольник - геометрия мироздания и инструмент познания" доступна на http://grani.agni-age.net/articles2/andreev.htm В ней автор самым неожиданным образом связывает числа Пи и Фи (золотое сечение) с пирамидой Хеопса, Ветхозаветным Енохом как носителем магической цифрой семь, построением семиугольника и прочими эзотерическими изысками.

Нет смысла цитировать фрагменты - зайдите и прочтите лично.

Создатель странички http://laplas.narod.ru/numer_pi.htm предложил свою формулу для вычислния числа Пи.

Если N=10 000, и точность вычисления 500 значащих цифр, то получим следующее значение для "пи"
Пи = 3.14159235959337332640673822570842421870593265598024690
6552049683416344089789068475237805981571125029387686062
4673188325650310260348017353037507287559741891028695865
48197024241906686830981813108269063793022376385475028538
39385092453592019148747614349583130497832722636129106169
443221761920176454563831745851684321691766427896810965901
112798977399787102891355739487908433311450311756802892268
981078453770726294564316856435700374584201612826374912855
59273951738815850437806694754603297770690392403992688

На страничке известного форумчанам Андрея http://andrey.unitech.uz/programming/cs/pi/index.htm выложена статья об использовании... впрочем, читайте сами:

Число Пи

Довольно подробную информацию про число Пи, а так же множество интересных статей и материалов про число Пи, Вы можете найти здесь. Здесь же я предоставляю Вам возможность ознакомиться с мощным вычислительным потенциалом нового типа decimal (System.Decimal), включённого в .NET Framework.

Тип decimal

Новый тип в C# - 128-битный монстр вычислений decimal (в .NET Framework'е ему соответствует System.Decimal). Позволяет вычислять с точностью до 28-29 знаков (подробнее о значениях Вы можете узнать здесь). Нужно отметить неплохую скорость вычисления, вычисление происходит практически на той же скорости, что и при использовании типа double.

Приступаем к вычислениям!

Понятно, что обладая только одной точностью вычислений, ничего посчитать не удастся. Как это ни странно необходимо ещё и обладать алгоритмом вычисления. Для примера предлагаю взять ряд Лейбница:

ПИ = 4 - 4/3 + 4/5 - 4/7 + 4/9 - ... - 4/n + 4/(n+2)

Примечание: вообще-то ряд Лейбница выглядит как pi/4 = 1 - 1/3 + 1/5 - 1/7 ..., однако если обе части уравнения умножить на 4, получится вышестоящая строка.

Остаётся лишь написать программу, делающую это, что довольно не трудно - Вам нужно лишь создать консольный проект на C#, и вставить следующий код в файл Class1.cs (я проект назвал Picalc).

Через некоторое время (чем дольше будет программа работать - тем точнее будет Пи, максимум 28 знаков вычисления, у меня она работала около 2-х часов, затем я не вытерпел и нажал Ctrl+C) Вы сможете видеть что-то похожее на это:
Pi ~= 3,1415922535897932384786433576; i = 5000001;
Pi ~= 3,1415927869231087940199765815; i = 15000003;
Pi ~= 3,1415925735898060384607232875; i = 25000005;
Pi ~= 3,1415927107326405854030514414; i = 35000007;
Pi ~= 3,1415926091453566952513840285; i = 45000009;
Pi ~= 3,1415926899534229905299490471; i = 55000011;
Pi ~= 3,1415926228205681497042054871; i = 65000013;
Pi ~= 3,141592680256454927352456658; i = 75000015;
Pi ~= 3,1415926300603859028216745075; i = 85000017;
Pi ~= 3,1415926746424208284910976858; i = 95000019;
Pi ~= 3,1415926345421778189608202485; i = 105000021;
Pi ~= 3,1415926709810942592572293024; i = 115000023;
Pi ~= 3,1415926375897963104620544466; i = 125000025;
Pi ~= 3,1415926684046052000544127793; i = 135000027;
Pi ~= 3,1415926397966924536821057459; i = 145000029;
Pi ~= 3,141592666493016547516195921; i = 155000031;
Pi ~= 3,1415926414685834680305994022; i = 165000033;
Pi ~= 3,1415926650183624466263398273; i = 175000035;
Pi ~= 3,14159264277898453137677054; i = 185000037;
Pi ~= 3,1415926638462014961882134421; i = 195000039;
Pi ~= 3,1415926438336975811154547435; i = 205000041;
Pi ~= 3,1415926628921170026598613498; i = 215000043;
Pi ~= 3,1415926447009060878450196187; i = 225000045;
Pi ~= 3,1415926621004298704231322748; i = 235000047;
Pi ~= 3,1415926454265295316734922878; i = 245000049;
Pi ~= 3,1415926614329289554948556662; i = 255000051;
Pi ~= 3,1415926460426249080956744134; i = 265000053;
Pi ~= 3,1415926608625190830910229231; i = 275000055;
Pi ~= 3,1415926465722507576990608556; i = 285000057;
Pi ~= 3,1415926603694529224617564075; i = 295000059;
Pi ~= 3,1415926470324174792578749163; i = 305000061;
Pi ~= 3,1415926599389983379841793441; i = 315000063;
Pi ~= 3,1415926474359482964505706154; i = 325000065;
Pi ~= 3,1415926595599413159857087509; i = 335000067;
Pi ~= 3,1415926477926929318041531249; i = 345000069;
Pi ~= 3,1415926592235949444735745891; i = 355000071;
Pi ~= 3,1415926481103422645461232793; i = 365000073;

Здесь под "i" имеется ввиду число - последний знаменатель ряда (4/i).

Если в 40-ой строке программы (if(i%5000001==0)) вместо числа 5000001 поставить 5001, то можно увидеть как ряд сближается в самом начале:

Pi ~= 3,1411926536057932352626449479; i = 5001;
Pi ~= 3,1417259691471264927757294533; i = 15003;
Pi ~= 3,1415126663878735046688553525; i = 25005;
Pi ~= 3,1416497866526501174710502723; i = 35007;
Pi ~= 3,1415482170452008838422690501; i = 45009;
Pi ~= 3,141629010615776497567014979; i = 55011;
Pi ~= 3,1415618900384561498950727651; i = 65013;
Pi ~= 3,141619315279606401034274581; i = 75015;
Pi ~= 3,1415691286062639817630210862; i = 85017;
Pi ~= 3,1416137022332058389941775983; i = 95019;
Pi ~= 3,1415736095981743214640558846; i = 105021;
Pi ~= 3,1416100415677439681414128899; i = 115023;
Pi ~= 3,1415766566612045510975143736; i = 125025;
Pi ~= 3,1416074655519330508164774733; i = 135027;
Pi ~= 3,1415788631493272256108086235; i = 145029;
Pi ~= 3,1416055543186838840512201359; i = 155031;
Pi ~= 3,1415805347279971833545771071; i = 165033;
Pi ~= 3,1416040799412445834541665152; i = 175035;
Pi ~= 3,1415818448822987963761242388; i = 185037;
Pi ~= 3,141602908001753715003203042; i = 195039;
Pi ~= 3,1415828993954899199499300034; i = 205041;
Pi ~= 3,1416019540985308652995804079; i = 215043;
Pi ~= 3,1415837664388362677845806995; i = 225045;
Pi ~= 3,1416011625625048089581706294; i = 235047;
Pi ~= 3,1415844919235075854738341565; i = 245049;
Pi ~= 3,1416004951894794539288546426; i = 255051;
Pi ~= 3,1415851079006455560030217034; i = 265053;
Pi ~= 3,1415999248892470677619887; i = 275055;
Pi ~= 3,1415856374245486009643531129; i = 285057;
Pi ~= 3,1415994319181218281878246538; i = 295059;
Pi ~= 3,1415860975024662257147922045; i = 305061;
Pi ~= 3,141599001546703243006896692; i = 315063;
Pi ~= 3,1415865009552351789034673507; i = 325065;
Pi ~= 3,1415986225630700919353293911; i = 335067;
Pi ~= 3,1415868576307359419198480378; i = 345069;
Pi ~= 3,1415982862819384045887300654; i = 355071;

Теперь - как запомнить число Пи. В дополнение к рекордсменам по запоминанию, представленных в разделе Олега Степанова, приведем статью

В.Козаренко "Как запомнить число ПИ"

источник - http://mnemotexnika.narod.ru/sport_01.htm  

Мнемонисты любят запоминать число ПИ. И соревнуются в количестве запоминаемых цифр этого бесконечного числа. Рекордсмены разных стран занесены в книгу рекордов.

Японец Хидеаки Томойори может воспроизвести число ПИ до 40 000 знаков. На запоминание такого количество цифр у него ушло около 10 лет.

Российский рекорд по запоминанию числа ПИ много скромнее. Челябинец Александр Беляев воспроизвел 2500 знаков числа ПИ. На припоминание цифр он затратил полтора часа. На запоминание - полтора месяца. До этого рекорд России был «всего» 2000 знаков. У вас есть реальные шансы побить российский рекорд, так как запомнить 3-4 тысячи цифр не так уж и сложно. Было бы желание.

Почему именно число ПИ, а не ряд случайных чисел?
Мнемонисты запоминают число ПИ по одной простой причине. Если бы они воспроизводили просто ряд случайных чисел, то могут возникнуть подозрения, что человек не запомнил эти числа, а воспроизводит их по какой-нибудь системе. Например, называет любое случайное число, затем прибавляет 13 и называет две последние цифры, затем отнимает 9 и называет две последние цифры. Или что-нибудь другое в этом же роде.

Но когда человек воспроизводит бесконечное число ПИ, то всякие подозрения о нечестности запоминателя отпадают. Очевидно, что никакой закономерности в следовании цифр в числе ПИ нет. И единственный способ воспроизвести эти цифры - это запомнить их.

Для чего запоминают такое количество цифр?
Не только ради установления мирового рекорда. Не только для рекламы школы, в которой читаются курсы по технике запоминания. Не только ради славы (книга рекордов - это книга рекордов).
Число ПИ обычно запоминают для тренировки. Что тренируется при выполнении такого необычного упражнения?

Первое. Мнемонист оттачивает, отшлифовывает образные коды чисел - зрительные образы, которыми обозначается двузначное число (их всего сто) или трехзначное число (этих образных кодов 1000).

Второе. Мнемонист отрабатывает основную операцию запоминания - соединение зрительных образов в воображении. Чтобы запомнить несколько тысяч цифр, нужно образовать соответствующее количество связей между образами.

Третье. Мнемонист закрепляет в своей памяти большое количество вспомогательных образов, которые в разных системах называются по разному - локи, опорные образы, стимулирующие образы, вешалки и т.д.

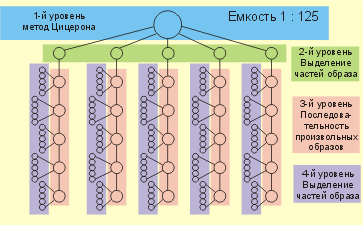
Четвертое. Мнемонист отрабатывает разные способы фиксации последовательности образов. Длинный ряд чисел может быть разбит на фрагменты, каждый из которых запомнен разными методами. В результате, можно лично убедиться в том, какой метод запоминания более надежен с точки зрения долговременного запоминания. И более рационален с точки зрения запоминания числовой информации.

Ниже мы рассмотрим один из способов запоминания числа ПИ. Хотя, конечно же, способов запоминания может быть много. Если у вас есть свой оригинальный способ запоминания числа ПИ, вы можете рассказать о нем читателям сайта «Mnemonikon» в разделе «Дискуссии». Лично я знаю много способов запоминания этого числа. И, возможно, в обновлениях сайта мы продолжим эту интересную тему.

Для начала приведем само число ПИ, рассчитанное с точностью до 20 000. Это и будет наше суперупражнение для тренировки.

3.14159265358979323846264338327950
28841971693993751058209749445923
07816406286208998628034825342117
06798214808651328230664709384460
95505822317253594081284811174502
84102701938521105559644622948954
93038196442881097566593344612847
56482337867831652712019091456485
66923460348610454326648213393607
26024914127372458700660631558817
48815209209628292540917153643678
92590360011330530548820466521384
(для ускорения закачки страницы сокращены знаки числа Пи - для тренировки смотрите их в первом зале музея Пи Е.С.)

Способ запоминания числа ПИ

(Четырехуровневая система опорных образов, емкостью 1:125. Кодирование цифр - в образные коды двузначных чисел.)

Проведем предварительные расчеты. Если 20000 цифр запоминать с помощью образных кодов двузначных чисел, то вам придется запомнить 10 тысяч образов. Самый надежный способ запоминания образных кодов - это запоминать их на заранее подготовленную систему опорных образов. Следовательно, потребуется подготовить десять тысяч опорных образов. Где же их столько взять?

Основная проблема в данном случае заключается не в запоминании самих цифр числа ПИ, а в подготовке вспомогательных образов, на которые число ПИ будет запоминаться.

Во-первых, совершенно не обязательно формировать 10000 опорных образов сразу. Вы можете разбить процесс запоминания на части. И запоминать по 500 образов в день (по 1000 цифр числа ПИ). А можете запоминать и еще более маленькими «порциями».

Не следует забывать и о том, что любые вновь запомненные сведения необходимо закреплять путем их мысленной «прогонки». На это так же затрачивается время.

Для формирования большого количества опорных образов следует использовать комбинацию нескольких способов запоминания последовательности. При этом нужно подобрать эти способы так, чтобы вы имели возможность постепенно достраивать систему опорных образов.

В первом способе я предлагаю использовать многоуровневую систему опорных образов.

Первый уровень - образы, выделенные методом Цицерона. Представьте коридор своей квартиры и вспомните последовательно 10 предметов в нем.

Второй уровень. В каждом полученном образе выделите по пять частей. Пример. Если взять первым образом «дверь», то ее можно мысленно разобрать на части: петля, номерок, глазок, ручка, замок. В результате на втором уровне мы получили уже 5 опорных образов.

Третий уровень. Последовательность произвольных образов. Подберите любые пять образов и свяжите их приемом «Цепочка». Пример: голубь - клавиатура - сотовый телефон - магнитофон -дерево. Нужно запомнить пять таких цепочек. Каждая цепочка привязывается к образу второго уровня. В нашем примере к образу «петля» следует привязать связью первый образ цепочки «голубь». В результате на третьем уровне мы получим уже 25 образов.

Четвертый уровень. Каждый из 25 образов третьего уровня разбирается на пять частей. Пример. В образе «голубь» выделите образы: клюв, глаз, крыло, лапа, хвост. Аналогичные действия проделайте и с остальными 25 образами третьего уровня.

Многоуровневые системы опорных образов - одна из отличительных особенностей системы запоминания "Джордано"

В результате на четвертом уровне будет 125 опорных образов. Эти образы - конечные образы в системе опорных образов. Именно к ним будут привязываться запоминаемые числа.

На одной двери в своем коридоре вы сможете зафиксировать 125 чисел или 250 цифр числа ПИ.

На десяти образах, выделенных в коридоре, вы сможете зафиксировать 1250 двузначных чисел или 2500 цифр числа ПИ.

Если опорные образы сформированы - на это может уйти целый день - и если вы хорошо знаете образные коды двузначных чисел, то сам процесс запоминания двух с половиной тысяч цифр числа ПИ займет время равное 1250 умноженное на 6 секунд. Это 125 минут или примерно 2 часа. К этому времени, однако, можно смело прибавить еще 2 часа, необходимые для повторения информации и для устранения ошибок. Если ваша скорость запоминания ниже нормативной, то на запоминание 2500 цифр может уйти и целый день.

В четырех комнатах своей квартиры вы сможете разместить 10000 цифр числа ПИ.

Я рекомендую именно такой способ запоминания. Хотя могут быть и другие варианты. После «сдачи» рекорда, в вашем мозге останется 2500-5000 хорошо закрепленных опорных образов. А это намного важнее, чем воспроизведение числа ПИ. Эти опорные образы вы сможете в дальнейшем использовать для запоминания любой нужной вам информации.

Упражнение на запоминание числа ПИ, следует расценивать, в первую очередь, как упражнение на формирование системы опорных образов. Многоуровневая система опорных образов очень удобна для перемещения по информации в памяти, а также дает возможность системного и тематического запоминания - информация организуется в памяти буквально как в папках компьютера.

По легендам, мнемонисты средневековья "форматировали" свою память на 300000 опорных образов.

Еще раз хочу обратить ваше внимание на то, что емкость памяти мнемониста ограничена только системой заранее сформированных опорных образов. Мозг запоминает только связи. И новая информация запоминается на старую информацию - на заранее заученный стимулирующий образ. Система опорных образов - это система внутренней стимуляции мозга, позволяющая последовательно просматривать запомненные ранее сведения. Интересно и то, что даже при изменении состояния сознания (в состоянии опьянения, например) вы сможете безошибочно считывать информацию из мозга, благодаря системе опорных образов, которые не зависят от изменений в работе «входных» систем мозга (зрение, слух и так далее).

Да, мы не разобрали как, собственно, запоминать сами числа? Очень просто, как обычно. Разбейте цифровой ряд на двузначные числа, преобразовывайте двузначные числа в образные коды и последовательно связывайте с подготовленными опорными образами.

3. 14-15-92-65-35-89-79-32-38-46-26-43-38-32-79-...

3. Жучок-губы-радио-лупа-куб-фара-сыр-кит-хвоя-чашка-душ-очки-...

(Первую цифру "3" можно не запоминать, как-нибудь вспомните...)

О числе Пи ( А.В.Жукову)
Serg Merisarov

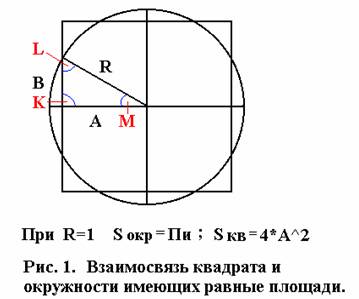
В заключение о новых методах вычисления Пи от Александра Новикова. http://www.nauka.lucksite.com/hipot/pi_an.html Я имел с Александром длительную переписку, предлагаю посетителям самим сделать заключение о его методах вычисления Пи. В одном из Ломтиков я упоминал этого автора. Привожу одну из его гипотез, присланную мне для заключения.

ГИПОТЕЗА. БОЛЕЕ ПРОСТОЙ МЕТОД РАСЧЁТА ЧИСЛА ПИ.

Существует доказательство того, что площадь окружности равна площади квадрата (Рис.1.) при угле М равном 27 градусов 36 минут.

Если данное доказательство достоверно, то тогда значение числа Пи можно рассчитать следующим образом: Косинусом угла М в треугольнике со сторонами АВR является отношение прилежащего катета А к гипотенузе R: cosM=A\R => A=R*cosM=1*cosM=cos27”36’=0,8878 Пи=Sокр=Sкв=4*А^2=4*0,8878^2=4*0,788189=3,152756
Полученный результат отличается от современного значения числа Пи равное 3,1415926. Хотя он немного и меньше значения 3,1547005 полученного в статье «Расчёт числа Пи», но тем не менее намного ближе к нему по своему значению.

Я ответил, что нелогично использовать готовое значение косинуса, найденное, отталкиваясь от известного значения Пи. Хотя, конечно, идея довольно занимательна.

Это пока все