Ломтик невозможный
Потому что попалась такая
картинка:

Рассмотрите ее внимательно - на
первый взгляд ничего особенного - берем лобзик
и... впрочем, и на второй взгляд ничего
особенного... как думаете - можно сделать в реале? Источник на нидерландском
языке :)

В ломтике
паркетном было опубликовано письмо Андрея
Василькова, в котором он обзывал меня всякими
словами (шучу) за предположение о том, что белок в
живых организмах имеет спиральную ориентацию. В
защиту моей позиции хочется привести сообщение,
найденное здесь:
Воссоздан самый
первый этап эволюции жизни на Земле
Группа Грэма Кукса из
Университета Пердью (Уэст-Лафайетт, штат Индиана)
выяснила, почему первые "строительные
блоки" биологических молекул имели
левостороннюю ориентацию. По-видимому, данная
работа позволит яснее понять "принципы
действия" живых организмов.
Как известно, аминокислоты, не
входящие в состав белков, могут быть
"закручены" как влево, так и вправо. И
"левые", и "правые" молекулы имеют
одинаковые химические свойства, вне зависимости
от ориентации, или, как говорят специалисты,
хиральности. Возможно, левосторонние
аминокислоты вошли в состав живой материи
совершенно случайно. Однако некоторые ученые
предполагают, что выбор природы пал на
левосторонние молекулы из-за того, что те
отличаются от правосторонних "сородичей"
какими-то особыми, пока не изученными свойствами.
Недавно группе Кукса удалось найти тому
подходящее доказательство. Серия экспериментов
продемонстрировала, что левосторонняя
"версия" аминокислоты под названием серин
способна укомплектовывать крупные пептидные
блоки соответствующей направленности.
Как выяснилось, молекулы
"левого" серина способны легко
формироваться в цепочки, в которых каждое звено
прочно связано друг с другом. Левосторонние
сериновые кластеры, в свою очередь, "сами
собой" соединяются с другими левосторонними
аминокислотами. Правосторонний серин, по мнению
ученых, не обладает способностями формировать
прочные связи и поэтому не обладает столь
выраженными "конструкторскими
способностями".
Возможно, формирование
"первичного бульона" началось с активной
деятельности левосторонних молекул серина. По
словам Кукса, обладающая необычными свойствами
аминокислота получила "партнеров для танца
жизни" и вместе с ними положила начало
биологической эволюции. Впоследствии
сформировавшиеся крупные биологические
молекулы - белки - последовали курсом, заданным
"левым" серином. Результаты экспериментов
также позволяют предположить, что серином была
определена хиральность и других биомолекул,
например, сахаров.
"Серин способен менять
хиральность при особых условиях окружающей
среды, - объясняет Кукс. - Если подвергнуть
правосторонние молекулы аминокислоты
воздействию поляризованного света, некоторые из
них станут левосторонними. Подобное явление
могло запустить химические реакции, которые
через миллиарды лет привели к возникновению
жизни". |
Впрочем, речь кажется не
о белке, но это уже не так важно по сравнению с
обязательной ориентацией. И по сравнению с
приятным впечатлением от знакомства - Андрей
давний (по)читатель Терры, я часто видел его ник {Alt}.ru-ist в Вопросе недели. Кроме
того Андрей продвигает Терру+ в Волгограде,
хорошо знаком с Наблюдателем (который сделал
Арбузный Форум и поддерживает арбуз-уз) и ведет
страницу, посвященную защите в Сети http://angstroem.t-k.ru/, которой в
сентябре исполняется три года. Поздравляем!
(Вообще 2000й был урожайным на хорошие проекты... :) )

Арбузные новости...
1 . Выложена статья "Преджизнь"
о происхождении жизни
2. Выложены Записки жизнелюба
3.Фигуры Лиссажу
4.Зеркальная симметрия в нашем мире
5. Обновил Законы Мэрфи - прислал
мой тезка, спасибо...
Еще один узор Лиссажу: Не правда ли
нечто объемное просматривается? Сплошные уши...

Смотрите также фигуры Лиссажу,
полученные участниками арбузного Форума, в том
числе и цветные и с рожицами...

Неоднократно цитированный Стас
снова пишет в
своем ЖЖ потрясающе интересные вещи, глупо
переписывать чужой ЖЖ, но эта тема настолько
"арбузная", что просто ссылкой ограничиться
не получится. Тем более, что на этот постинг мне
указали в Форуме Узнета с просьбой
прокомментировать - ведь вопросом о самом
большом числе задавался любой мыслящий человек.
Самое большое число в мире
В детстве меня мучил вопрос, какое существует
самое большое число, и я изводил этим дурацким
вопросом практически всех подряд. Узнав число
миллион, я спрашивал, а есть ли число больше
миллиона. Миллиард? А больше миллиарда? Триллион?
А больше триллиона? Наконец, нашёлся кто-то умный,
кто мне объяснил, что вопрос глуп, так как
достаточно всего лишь прибавить к самому
большому числу единицу, и окажется, что оно
никогда не было самым большим, так как существуют
число ещё больше.
И вот, спустя много лет, я решил задаться другим
вопросом, а именно: какое существует самое
большое число, которое имеет собственное
название? Благо, сейчас есть инет и озадачить
им можно терпеливые поисковые машины, которые не
будут называть мои вопросы идиотскими ;-).
Собственно, это я и сделал, и вот, что в результате
выяснил.
| Число |
Латинское название |
Русская приставка |
| 1 |
unus |
ан- |
| 2 |
duo |
дуо- |
| 3 |
tres |
три- |
| 4 |
quattuor |
квадри- |
| 5 |
quinque |
квинти- |
| 6 |
sex |
сексти- |
| 7 |
septem |
септи- |
| 8 |
octo |
окти- |
| 9 |
novem |
нони- |
| 10 |
decem |
деци- |
Существуют две системы наименования чисел —
американская и английская.
Американская система постороена довольно
просто. Все названия больших чисел строятся так:
в начале идет латинское порядковое числительное,
а в конце к ней добавляется суффикс -иллион.
Исключение составляет название "миллион"
которое является названием числа тысяча (лат. mille)
и увеличительного суффикса -иллион (см. таблицу).
Так получаются числа — триллион, квадриллион,
квинтиллион, секстиллион, септиллион, октиллион,
нониллион и дециллион. Американская система
используется в США, Канаде, Франции и России.
Узнать количество нулей в числе, записанном по
американской системе, можно по простой формуле
3·x+3 (где x - латинское числительное).
Английская система наименования наиболее
распространена в мире. Ей пользуются, например, в
Великобритании и Испании, а также в большинстве
бывших английских и испанских колоний. Названия
чисел в этой системе строятся так: так: к
латинскому числительному добавляют суффикс
-иллион, следущее число (в 1000 раз большее)
строится по принципу — то же самое
латинское числительное, но суффикс — -иллиард.
То есть после триллиона в английской системе
идёт триллиард, а только затем квадриллион, за
которым следует квадриллиард и т.д. Таким
образом, квадриллион по английской и
американской системам — это совсем разные
числа! Узнать количество нулей в числе,
записанном по английской системе и
оканчивающегося суффиксом -иллион, можно по
формуле 6·x+3 (где x - латинское числительное) и
по формуле 6·x+6 для чисел, оканчивающихся на
-иллиард.
Из английской системы в русский язык перешло
только число миллиард (10 9), которое всё же
было бы правильнее называть так, как его называют
американцы — биллионом, так как у нас принята
именно американская система. Но кто у нас в
стране что-то делает по правилам! ;-) Кстати,
иногда в русском языке употребляют и слово
триллиард (можете сами в этом убедиться,
запустив поиск в Гугле или Яндексе) и означает оно, судя по
всему, 1000 триллионов, т.е. квадриллион.
Кроме чисел, записанных при помощи латинских
префиксов по американской или англйской системе,
известны и так называемые внесистемные числа,
т.е. числа, которые имеют свои собственные
названия безо всяких латинских префиксов. Таких
чисел существует несколько, но подробнее о них я
расскажу чуть позже.
Вернемся к записи при помощи латинских
числительных. Казалось бы, что ими можно
записывать числа до бессконечности, но это не
совсем так. Сейчас объясню почему. Посмотрим для
начала как называются числа от 1 до 10 33:
| Название |
Число |
| Единица |
10 0 |
| Десять |
10 1 |
| Сто |
10 2 |
| Тысяча |
10 3 |
| Миллион |
10 6 |
| Миллиард |
10 9 |
| Триллион |
10 12 |
| Квадриллион |
10 15 |
| Квинтиллион |
10 18 |
| Секстиллион |
10 21 |
| Септиллион |
10 24 |
| Октиллион |
10 27 |
| Нониллион |
10 30 |
| Дециллион |
10 33 |
И вот, теперь возникает вопрос, а что
дальше. Что там за дециллионом? В принципе, можно,
конечно же, при помощи объединения приставок
породить такие монстры, как: андецилион,
дуодециллион, тредециллион, кваттордециллион,
квиндециллион, сексдециллион, септемдециллион,
октодециллион и новемдециллион, но это уже будут
составные названия, а нам были интересны именно
собственные названия чисел. Поэтому собственных
имён по этой системе, помимо указанных выше, ещё
можно получить лишь всего три
— вигинтиллион (от лат. viginti —
двадцать), центиллион (от лат. centum — сто) и
миллеиллион (от лат. mille — тысяча). Больше
тысячи собственных названий для чисел у римлян
не имелось (все числа больше тысячи у них были
составными). Например, миллион (1 000 000) римляне
называли decies centena milia, то есть "десять сотен
тысяч". А теперь, собственно, таблица:
| Название |
Число |
| Вигинтиллион |
10 63 |
| Центиллион |
10 303 |
| Миллеиллион |
10 3003 |
Таким образом, по подобной системе
числа больше, чем 10 3003, у которого было бы
собственное, несоставное название получить
невозможно! Но тем не менее числа больше
миллеиллиона известны — это те самые
внесистемные числа. Расскажем, наконец-то, о них.
| Название |
Число |
| Мириада |
10 4 |
| Гугол |
10 100 |
| Асанкхейя |
10 140 |
| Гуголплекс |
10 10100 |
| Второе число Скьюза |
10 10 10 1000 |
| Мега |
2[5] (в нотации Мозера) |
| Мегистон |
10 [5] (в нотации Мозера) |
| Мозер |
2[2[5]] (в нотации Мозера) |
| Число Грэма |
G63 (в нотации Грэма) |
| Стасплекс |
G100 (в нотации Грэма) |
Самое маленькое такое число — это мириада
(оно есть даже в словаре Даля), которое означает
сотню сотен, то есть — 10 000. Слово это, правда,
устарело и практически не используется, но
любопытно, что широко используется слово
"мириады", которое означает вовсе не
определённое число, а бесчисленное, несчётное
множество чего-либо. Считается, что слово мириада
(англ. myriad) пришло в европейские языки из древнего
Египта.
Гугол (от англ. googol) — это число десять в
сотой степени, то есть единица со ста нулями. О
"гуголе" впервые написал в 1938 году в статье
"New Names in Mathematics" в январском номере журнала
Scripta Mathematica американский математик Эдвард Каснер
(Edward Kasner). По его словам, назвать "гуголом"
большое число предложил его девятилетний
племянник Милтон Сиротта (Milton Sirotta).
Общеизвестным же это число стало благодаря,
названной в честь него, поисковой машине Google.
Обратите внимание, что "Google" — это торговая
марка, а googol — число.
В известном буддийском трактате Джайна-сутры,
относящегося к 100 г. до н.э., встречается число асанкхейя
(от кит. асэнци — неисчислимый), равное 10 140.
Считается, что этому числу равно количество
космических циклов, необходимых для обретения
нирваны.
Гуголплекс (англ. googolplex) - число также
придуманное Каснером со своим племянником и
означающее единицу с гуголом нулей, то есть 10 10100.
Вот как сам Каснер описывает это "открытие":
Words of wisdom are spoken by children at least as often as by scientists. The name
"googol" was invented by a child (Dr. Kasner's nine-year-old nephew) who was
asked to think up a name for a very big number, namely, 1 with a hundred zeros after it.
He was very certain that this number was not infinite, and therefore equally certain that
it had to have a name. At the same time that he suggested "googol" he gave a
name for a still larger number: "Googolplex." A googolplex is much larger than a
googol, but is still finite, as the inventor of the name was quick to point out.
Mathematics and the Imagination (1940) by Kasner and James R.
Newman.
Еще большее, чем гуголплекс число — число
Скьюза (Skewes' number) было предложено Скьюзом в 1933
году (Skewes. J. London Math. Soc. 8, 277-283, 1933.) при
доказательстве гипотезы
Риманна, касающейся простых чисел. Оно
означает e в степени e в степени e в
степени 79, то есть eee79. Позднее,
Риел (te Riele, H. J. J. "On the Sign of the Difference П(x)-Li(x)."
Math. Comput. 48, 323-328, 1987) свел число Скьюза к ee27/4,
что приблизительно равно 8,185·10 370. Понятное
дело, что раз значение числа Скьюза зависит от
числа e, то оно не целое, поэтому
рассматривать мы его не будем, иначе пришлось бы
вспомнить другие ненатуральные числа — число
пи, число e, число Авогадро и т.п.
Но надо заметить, что существует второе число
Скьюза, которое в математике обозначается как Sk2,
которое ещё больше, чем первое число Скьюза (Sk1).
Второе число Скьюза, было введённо Дж.
Скьюзом в той же статье для обозначения числа, до
которого гипотеза Риманна справедлива. Sk2
равно 101010103, то есть 1010101000
.
Как вы понимаете чем больше в числе степеней,
тем сложнее понять какое из чисел больше.
Например, посмотрев на числа Скьюза, без
специальных вычислений практически невозможно
понять, какое из этих двух чисел больше. Таким
образом, для сверхбольших чисел пользоваться
степенями становится неудобно. Мало того, можно
придумать такие числа (и они уже придуманы), когда
степени степеней просто не влезают на страницу.
Да, что на страницу! Они не влезут, даже в книгу,
размером со всю Вселенную! В таком случае встаёт
вопрос как же их записывать. Проблема, как вы
понимаете разрешима, и математики разработали
несколько принципов для записи таких чисел.
Правда, каждый математик, кто задавался этой
проблемой придумывал свой способ записи, что
привело к существованию нескольких, не связанных
друг с другом, способов для записи чисел — это
нотации Кнута, Конвея, Стейнхауза и др.
Рассмотрим нотацию Хьюго Стенхауза (H. Steinhaus. Mathematical
Snapshots, 3rd edn. 1983), которая довольно проста. Стейн
хауз предложил записывать большие числа внутри
геометрических фигур — треугольника, квадрата и
круга:
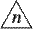 — означает nn. — означает nn.
 — означает
"n в n треугольниках". — означает
"n в n треугольниках". 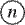 — означает
"n в n квадратах". — означает
"n в n квадратах".
Стейнхауз придумал два новых сверхбольших
числа. Он назвал число 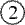 — Мега, а число — Мега, а число  — Мегистон. — Мегистон.
Математик Лео Мозер доработал нотацию
Стенхауза, которая была ограничена тем, что если
требовалаось записывать числа много больше
мегистона, возникали трудности и неудобства, так
как приходилось рисовать множество кругов один
внутри другого. Мозер предложил после квадратов
рисовать не круги, а пятиугольники, затем
шестиугольники и так далее. Также он предложил
формальную запись для этих многоугольников,
чтобы можно было записывать числа, не рисуя
сложных рисунков. Нотация Мозера выглядит так:
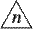 = "n
треугольнике" = nn = n[3]. = "n
треугольнике" = nn = n[3].  = "n в
квадрате" = n[4] = "n в n
треугольниках" = n[3]n. = "n в
квадрате" = n[4] = "n в n
треугольниках" = n[3]n. 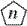 = "n в
пятиугольнике" = n[5] = "n в n
квадратах" = n[4]n. = "n в
пятиугольнике" = n[5] = "n в n
квадратах" = n[4]n. - n[k+1] = "n в n k-угольников"
= n[k]n.
Таким образом, по нотации Мозера
стейнхаузовский мега записывается как 2[5], а
мегистон как 10[5]. Кроме того, Лео Мозер предложил
называть многоугольник с числом сторон равным
меге — мегагоном. И предложил число "2 в
Мегагоне", то есть 2[2[5]]. Это число стало
известным как число Мозера (Moser's number) или просто
как мозер.
Но и мозер не самое большое число. Самым большим
числом, когда-либо применявшимся в
математическом доказательстве, является
предельная величина, известная как число Грэма
(Graham's number), впервые использованная в 1977 года в
доказательстве одной оценки в теории Рамсея. Оно
связано с бихроматическими гиперкубами и не
может быть выражено без особой 64-уровневой
системы специальных математических символов,
введённых Кнутом в 1976 году.
К сожалению, число записанное в нотации Кнута
нельзя перевести в запись по системе Мозера.
Поэтому придётся объяснить и эту систему. В
принципе в ней тоже нет ничего сложного. Дональд
Кнут (да, да, это тот самый Кнут, который написал
"Искусство программирования" и создал
редактор TeX) придумал понятие сверхстепень,
которое предложил записывать стрелками,
направленными вверх:
- 2
  3 = 222. 3 = 222.
- 8
  4 = 8888. 4 = 8888.
- 2
   3 = 2 3 = 2  2 2  2 = 2 2 = 2  4 = 65536. 4 = 65536.
- Гугол = 10
 10 10 2. 2.
- Гоголплекс = 10гугол = 10
 10 10 10 10 2. 2.
В общем виде это выглядит так:
Думаю, что всё понятно, поэтому вернёмся к числу
Грэма. Грэм предложил, так называемые G-числа:
- G1 = 3
  .. ..  3, где число
стрелок сверхстепени равно 3 3, где число
стрелок сверхстепени равно 3    3. 3.
- G2 =
  .. ..  3, где число
стрелок сверхстепени равно G1. 3, где число
стрелок сверхстепени равно G1.
- G3 =
  .. ..  3, где число
стрелок сверхстепени равно G2. 3, где число
стрелок сверхстепени равно G2.
- ...
- G63 =
  .. ..  3, где число
стрелок сверхстепени равно G62. 3, где число
стрелок сверхстепени равно G62.
Число G63 стало называться числом
Грэма (обозначается оно часто просто как G).
Это число является самым большим известным в
мире числом и занесёно даже в "Книгу рекордов
Гинесса". А, вот тут
лежит доказательство, что число Грэма больше
числа Мозера.
P.S. Чтобы принести великую пользу
всему человечеству и прославиться в веках, я
решил сам придумать и назвать самое большое
число. Это число будет называться стасплекс и
оно равно числу G100. Запомните его, и когда
ваши дети будут спрашивать какое самое большое в
мире число, говорите им, что это число называется стасплекс. |
Первая мысль у каждого -
конечно же прибавить к стасплексу 1 и
назвать своим именем. Но будем честными - кто
кроме Стаса "двинул собой" чтобы разложить
все по полочке более ленивым нам? Так что
название этого числа его именем справедливо -
считаю, что каждый, кому оно попадется в расчетах,
именно так и должен его называть.:)
Поиск больших чисел у Гарднера не дал результата.
Есть эпизод у Гуго Штейнгауза в
"Математическом калейдоскопе" (библиотечка
Квант, Наука., М., 1981, стр 19), но он повторяет
сказанное у Стаса:
число МЕГА слишком большое, чтобы ему
можно было приписать какой-либо физический
смысл.
МЕГА=2 в кружочке=2 в двух квадратиках=2 в двух
треугольничках и в квадратике=22 в
треугольничке и в квадратике=44 в
квадратике=256 в квадратике=256 в 256
треугольничках=(256256)256 раз...
Потом Штейнгауз предлагает оценить число
МЕДЗОН=3 в кружочке.
Насчет времени (было в комментах
наподобие) в какой-то книжке ссылка на индийскую
легенду (возможно надуманная, а, может быть, и
правда), что раз в сто лет к алмазной скале
прилетает орел почистить клюв. Когда вся скала
сточится - пройдет одна секунда вечности... Можно
было бы прикинуть - взять стойкость алмаза,
режимы зачистки клюва... все равно получится
больше, чем прошло от Большого взрыва и появления
Вселенной - это 20*109 лет (кажется, точно не
помню - я тогда был маленький)
Впрочем, вопрос не в природе числа, а в названии.
Хорошо бы назать его словом из трех букв (фи,
поручик), чтобы можно было продолжить известную
игру - меняя по одной букве построить цепочку
слов
МИГ - ЧАС - ГОД - ВЕК - ЭРА - (новое слово, хотя бы БУЗ)

Фрагмент переписки с Артуром о
пропавшем сайте небезызвестной Апачи
> Знакомый Ваш
адрес, кажется, мы ранее переписывались
Угу, было дело... Мы с Вами так и не обсудили,
например, откуда
взялась эта кочующая из книги в книгу и из
программы в программу ошибка,
что множество Мандельброта лежит целиком внутри
окружности с радиусом 2.
Однако простейший эксперимент показывает, что
если проверку модуля
члена комплексной последовательности
ограничить числом 2, то картина
совсем не такая получается, чем если его
увеличить до, скажем, 3...
> и я был на Вашей Сплюшке, напомните, пожалуйста
url.
А его чрезвычайно просто получить - достаточно в
Яндексе или в Гугле
набрать в строке поиска слово "сплюшка" - он
будет на ПЕРВОМ месте
в списке результатов!
Недавно я обновил мой FAQ о фракталах. Он, конечно,
далек от совершенства,
но в нем представлено многое из того, что не дает
мне спать по ночам...
С уважением,
Артур
Итак, приглашаю всех на
замечательную Сплюшку http://splushka.narod.ru
не только посмотреть FAQ по фракталам, но и другие
не менее интересные материалы.
По существу вопроса о границах условия выхода из
итерационного цикла, порождающего фракталы,
утверждаю, что никогда не выбирал ее равной 2.
Наоборот - менял этот параметр в широчайших
пределах, добиваясь красивых картинок. Буду
благодарен всем "фрактальщикам" за участие
в обсуждении этого вопроса, прошу в Форум.

В развитие темы о цвете крови из ломтика рекомендательного -
получил письмо от Петра Глядкова:
"У всех людей
кровь красного цвета. Цвет ей, как известно,
придаёт гемоглобин" - а все ли так просто? Вот в
одном из романов Кусто (глава "Там, где льется
зеленая кровь") описано, как удивились
ныряльщики, когда порезав руку на глубине,
увидели вытекающую кровь зеленой. Может быть это
связано с неравномерным поглощением различных
частей спектра солнца при погружении, а может
быть дело в давлении. По их словам, кровь, которая
при максимальной глубине была зеленой, ближе к
поверхности стала бурой, а потом - красной.
Интересно - кто что думает?

Наверное одни математические
картинки утомительны для неокрепшей психики,
поэтому предлагаю отдохнуть взором на
фотографиях, любезно предоставленных арбузницей
с ником pailaps. По эстонски это означает
"паинька", но ник этот взят, по признанию его
носителя, скорее вопреки, чем по соответствию...

 
Как приятно смотреть на
аппетитно кушающего человека!!! Анти-паинька
пригласила на свою страницу
ЖЖ (а там и следующие интересные сылки...) и
познакомила с проектом
Дельфи - интернет-тусовка прибалтийцев.
Вообще-то Интернет без границ, но, вместе с тем,
популярны локальные образования... (Где-то
зависла моя статья об интернет-сообществах, там
все расписано, постараюсь выложить...)

Под занавес задачи - с помощью
программ решаются мгновенно - а как насчет
подумать головой? Первые три задачи специально
для суеверных :)
Найдите все трехзначные
числа, которое уменьшается в 13 раз при
вычеркивании средней цифры
Найдите наименьшее натуральное
число, которое оканчивается на 13, делится на 13 и
имеет сумму цифр, равную 13.
Сколько последовательных
натуральных чисел, начиная с 1, надо сложить,
чтобы получить трехзначное число, записываемое
одинаковыми цифрами?
Найдите наибольший общий
делитель всех девятизначных чисел, состоящих из
цифр 1,2,3,4.5.6,7,8,9 (без повторений).
|

Вот и все... The end типа... |







