Самая изумительная во всем Интернете страница - список интересных чисел, составленный ассоциативным профессором Университета Сетсона во Флориде Эриком Фридманом. Если вы знаете интересные сведения о числах, не отраженные в таблице, просьба посылать ее автору.

Я перевел на русский то, что с ходу понял и с любезного разрешения автора представляю "рунетчикам". Сложность не в переводе, а в знаниях различных областей математики. Буду рад всем, кто предложит свои толкования свойств чисел, не переведенных пока на русский.
Список разбит на 2 части.   Вторая часть здесь.  Цвета чисел соответствуют списку:

1 is the multiplicative identity. Дает тождество при умножении.
2 is the only even prime. Единственное четное простое число.
3 is the number of dimensions we live in. Число размерностей, в которых мы живем.
4 is the smallest number of colors sufficient to color all planar maps. Наименьшее число цветов для раскраски карты на плоскости.
5 is the number of Platonic solids. Число Платоновых многогранников.
6 is the smallest perfect number. Наименьшее совершенное число.
7 is the smallest number of integer-sided rectangles that tile a rectangle so that no 2 rectangles share a common dimension. ????
8 is the largest cube in the Fibonacci sequence. Наибольший куб в последовательности Фибоначчи.
9 is the maximum number of cubes that are needed to sum to any positive integer. Максимальное число кубов, необходимое для представления в виде их суммы любого положительного целого числа????
10 is the base of our number system. Основание нашей системы счисления
11 is the largest known multiplicative multiplicity.????
12 is the smallest abundant number.
13 is the number of Archimedian polyhedra.Число Архимедовых многогранников
14 is the smallest number n with the property that there are no numbers coprime to n smaller numbers.
15 is the smallest composite number n with the property that there is only one group of order n.
16 is the only number (besides 1) of the form x^y=y^x. Единственное число (кроме 1), выражаемое в форме x^y=y^x   , а именно 2⁴=4^2.
17 is the number of wallpaper patterns.
18 is the only number that is twice the sum of its digits.Единственное число, равное удвоенной сумме его цифр.
19 is the maximum number of 4^th powers needed to sum to any number.
20 is the number of rooted trees with 6 vertices.
21 is the smallest number of distinct squares needed to tile a square.
22 is the number of partitions of 8.
23 is the smallest number of integer-sided boxes that tile a box so that no two boxes share a common dimension.
24 is the largest number divisible by all numbers less than its square root. Самое большое число, которое делится на все числа, меньшие корня из него.
25 is the smallest square that can be written as a sum of 2 squares. Наименьшее число, которое можно представить как сумму двух квадратов.
26 is the smallest non-palindrome with a palindromic square. Наименьшее число не-палиндром, квадратом которого является палиндром.
27 is the largest number that is the sum of the digits of its cube. Наибольшее число, равное кубу суммы его цифр.
28 is the 2^nd perfect number. Второе совершенное число.
29 is the 7^th Lucas number.
30 is the largest number with the property that all smaller numbers coprime to it are prime.
31 is a Mersenne prime. Простое число Мерсенна.
32 is the smallest 5^th power (besides 1). Наименьшая 5-ая степень числа (исключая 1)
33 is the largest number that is not a sum of distinct triangular numbers.
34 is the smallest number with the property that it and its neighbors have the same number of divisors.
35 is the number of hexominoes. Количество плиток гексамино.
36 is the smallest number (besides 1) which is both square and triangular. Наименьшее число (кроме 1), которое одновременно и квадрат и треугольное.
37 is the maximum number of 5^th powers needed to sum to any number. Максимальное количество 5х степеней чисел, необходимое для выражения их суммой любого числа.
38 is the last roman numeral when written lexicographically.
39 is the smallest number which has 3 different partitions into 3 parts with the same product.
40 is the maximum number of spheres that can touch another sphere in a lattice packing in 5 dimensions.
41 is the smallest number that is not of the form |2^x - 3^y|.
42 is the 5^th Catalan number.
43 is the number of sided 7-iamonds.
44 is the number of derangements of 5 items.
45 is a Kaprekar number.
46 is the smallest number of vertices known in a planar 3-regular 3-connected graph with no Hamiltonian cycle.
47 is the largest number of cubes that cannot tile a cube.
48 is the smallest number with 10 divisors.
49 is the smallest number with the property that it and its neighbors are squareful.
50 is the smallest number that can be written as the sum of of 2 squares in 2 ways.
51 is the 6^th Motzkin number.
52 is the 5^th Bell number.
53 is a value of n with the property that n divides the sum of the first n primes.
54 is the smallest number that can be written as the sum of 3 squares in 3 ways.
55 is the largest triangular number in the Fibonacci sequence.
56 is the number of reduced 5 x 5 Latin squares.
57 = 111 in base 7.
58 is the number of commutative semigroups of order 4.
59 is the smallest number whose 4^th power is of the form a⁴+b⁴-c⁴.
60 is the smallest number divisible by 1 through 6.
61 is the 6^th Euler number.
62 is the smallest number that can be written as the sum of of 3 distinct squares in 2 ways.
63 is the number of partially ordered sets of 5 elements.
64 is the smallest number with 7 divisors.
65 is the smallest number that can be written as the sum of of 2 distinct squares in 2 ways.
66 is the number of 8-iamonds.
67 is the smallest number which is palindromic in bases 5 and 6.
68 is the last 2-digit string to appear in the decimal expansion of pi.
69 has the property that n² and n³ together contain each digit once.
70 is the smallest abundant number that is not the sum of some subset of its divisors.
71 divides the sum of the primes less than it.
72 is the maximum number of spheres that can touch another sphere in a lattice packing in 6 dimensions.
73 is the smallest number (besides 1) which is one less than twice its reverse.
74 ???
75 is the number of orderings of 4 objects with ties allowed.
76 is automorphic.
77 is the largest number that cannot be written as a sum of numbers whose reciprocals sum to 1.
78 is the smallest number that can be written as the sum of of 4 distinct squares in 3 ways.
79 is a permutable prime.
80 is the smallest number n where n and n+1 are both products of 4 or more primes.
81 is the square of the sum of its digits.
82 is the number of 6-hexes.
83 ???
84 is the largest order of a permutation of 14 elements.
85 is the largest n for which 1²+2²+3²+...+n² = 1+2+3+...+m has a solution.
86 = 222 in base 6.
87 ???
88 is the only number known whose square has no isolated digits.
89 = 8¹ + 9²
90 is the number of degrees in a right angle.
91 is the smallest pseudoprime in base 3.
92 is the number of essentially different placements of 8 non-attacking queens on a chessboard.
93 = 333 in base 5.
94 is a Smith number.
95 is the number of planar partitions of 10.
96 is the smallest number that can be written as the difference of two squares in 4 ways.
97 is the smallest number with the property that its first 3 multiples contain the digit 9.
98 is the smallest number with the property that its first 5 multiples contain the digit 9.
99 is a Kaprekar number.
100 is the smallest square which is also the sum of 4 consecutive cubes.
101 is the number of partitions of 13.
102 is the smallest number with three different digits.
103 has the property that placing the last digit first gives 1 more than triple it.
104 is the smallest known number of unit line segments that can exist in the plane, 4 touching at every vertex.
105 is the largest number n known with the property that n - 2^k is prime for k>1.
106 is the number of trees with 10 vertices.
107 is the exponent of a Mersenne prime.
108 is the hyperfactorial 3³ 2² 1¹.
109 is the smallest number which is palindromic in bases 5 and 9.
110 is the smallest number that is the product of two different substrings.
111 is the smallest possible magic constant of a 3 x 3 magic square of distinct primes.
112 is the side of the smallest square that can be tiled with distinct integer-sided squares.
113 is a permutable prime.
114 = 222 in base 7.
115 is the number of rooted trees with 8 vertices.
116 ???
117 ???
118 is the smallest number that has 4 different partitions into 3 parts with the same product.
119 is the smallest number n where either n or n+1 is divisible by the numbers from 1 to 8.
120 is the smallest number to appear 6 times in Pascal's triangle.
121 is the only square known of the form 1+p+p²+p³+p⁴, where p is prime.
122 ???
123 is the 10^th Lucas number.
124 is the smallest number with the property that its first 3 multiples contain the digit 2.
125 is the only number known (other than 1) that contains all its divisors as substrings.
126 = ₉C₄.
127 is a Mersenne prime.
128 is the largest number which is not the sum of distinct squares.
129 is the smallest number that can be written as the sum of 3 squares in 4 ways.
130 is the number of functions from 6 unlabeled points to themselves.
131 is a permutable prime.
132 is the smallest number which is the sum of all of the 2-digit numbers that can be formed with its digits.
133 is the smallest number for which the sum of the proper divisors divides phi(n).
134 = ₈C₁ + ₈C₃ + ₈C₄.
135 = 1¹ + 3² + 5³.
136 ???
137 is the maximum number of 7^th powers that are needed to sum to any arbitrarily large number.
138 ???
139 is the number of unlabeled topologies with 5 elements.
140 is the smallest harmonic divisor number.
141 is a Cullen number.
142 is the number of planar graphs with 6 vertices.
143 is the smallest quasi-Carmichael number in base 8.
144 is the largest square in the Fibonacci sequence.
145 = 1! + 4! + 5!
146 = 222 in base 8.
147 is the number of sided 6-hexes.
148 ???
149 ???
150 ???
151 is a palindromic prime.
152 ???
153 = 1³ + 5³ + 3³.
154 is the smallest number which is palindromic in bases 6, 8, and 9.
155 is the sum of the primes between its smallest and largest prime factor.
156 is the number of graphs with 6 vertices.
157 is the exponent of the smallest power that 2 that contains the digit string 666.
158 is the number of planar partitions of 11.
159 is the number of isomers of C₁₁H₂₄.
160 is the number of 9-iamonds.
161 ???
162 ???
163 has the property that e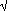¹⁶³ is within 10^-12 of an integer.
164 ???
165 = ₁₁C₃.
166 is the number of monotone Boolean functions of 4 variables.
167 ???
168 is the size of the smallest non-cyclic simple group which is not an alternating group.
169 is a square whose digits are non-decreasing.
170 ???
171 is a palindromic triangular number.
172 = 444 in base 6.
173 ???
174 ???
175 = 1¹ + 7² + 5³.
176 is an octagonal pentagonal number.
177 is the number of graphs with 7 edges.
178 ???
179 ???
180 is the total number of degrees in a triangle.
181 is a strobogrammatic prime.
182 is the number of connected bipartite graphs with 8 vertices.
183 ???
184 is a Karmekar number in base 3.
185 ???
186 is the number of degree 11 irreducible polynomials over GF(2).
187 is the smallest quasi-Carmichael number in base 7.
188 is the number of semigroups of order 4.
189 is a Karmekar number in base 2.
190 ???
191 is a palindromic prime.
192 is the smallest number with 14 divisors.
193 ???
194 is the smallest number that can be written as the sum of 3 squares in 5 ways.
195 ???
196 is the smallest number that is not known to reach a palindrome when repeatedly added to its reverse.
197 = 111 + 9 + 77.
198 = 11 + 99 + 88.
199 is the 11^th Lucas number.
200 ???
201 is a Karmekar number in base 4.
203 is the 6^th Bell number.
207 has a 4^th power where the first half of the digits are a permutation of the last half of the digits.
209 is the smallest quasi-Carmichael number in base 9.
210 is the product of the first 4 primes.
212 has a square with 4/5 of the digits are the same.
215 = 555 in base 6.
216 is the smallest cube that can be written as the sum of 3 cubes.
217 is a Karmekar number in base 2.
218 is the number of digraphs with 4 vertices.
219 is the number of space groups, not including handedness.
220 is the smallest amicable number.
221 is the number of Hamiltonian planar graphs with 7 vertices.
222 is the number of lattices on 10 unlabeled nodes.
225 is an octagonal square.
227 is the number of connected planar graphs with 8 edges.
228 = 444 in base 7.
230 is the number of space groups, including handedness.
231 is the number of partitions of 16.
232 is the number of 7x7 symmetric permutation matrices.
233 is the smallest number with the property that it and its neighbors can be written as a sum of 2 squares.
235 is the number of trees with 11 vertices.
237 is the smallest number with the property that its first 3 multiples contain the digit 7.
239 is the largest number that cannot be written as a sum of 8 or fewer cubes.
240 is the smallest number with 20 divisors.
242 is the smallest number n where n through n+3 are all products of 3 or more primes.
243 = 3⁵.
244 is the smallest number (besides 2) that can be written as the sum of two squares or the sum of two fifth powers.
246 = ₉C₂ + ₉C₄ + ₉C₆.
251 is the smallest number that can be written as the sum of 3 cubes in 2 ways.
252 is the 5^th central binomial coefficient.
254 is the smallest composite number all of whose divisors (except 1) contain the digit 2.
255 = 1111111 in base 2.
256 is the smallest 8^th power (besides 1).
257 is a Fermat prime.
259 = 1111 in base 6.
261 is the number of essentially different ways to dissect a 16-gon into 7 quadrilaterals.
262 is the 9^th meandric number.
264 is a non-palindrome with a palindromic square.
265 is the number of derangements of 6 items.
266 is the Stirling number of the second kind S(8,6).
267 is the number of planar partitions of 12.
270 is a harmonic divisor number.
272 is the 7^th Euler number.
273 = 333 in base 9.
274 is the Stirling number of the first kind s(6,2).
276 is the sum of the first 3 5^th powers.
282 is the sum of its proper divisors that contain the digit 4.
284 is amicable.
285 is the number of binary rooted trees with 13 vertices.
286 is the number of rooted trees with 9 vertices.
288 = 1¹ + 2² + 3³ + 4⁴.
289 is a square whose digits are non-decreasing.
291 is the number of functional digraphs on 8 vertices.
292 = 444 in base 8.
297 is a Kaprekar number.
301 is a 6-hyperperfect number.
302 is the number of acyclic digraphs with 5 vertices.
303 has a cube that is a concatenation of other cubes.
307 is a non-palindrome with a palindromic square.
311 is a permutable prime.
312 = 2222 in base 5.
313 is a palindromic prime.
315 = (4+3)(4+1)(4+5).
318 is the number of unlabeled partially ordered sets of 6 elements.
320 is the maximum determinant of a 10 x 10 matrix of 0's and 1's.
322 is the 12^th Lucas number.
323 is the product of twin primes.
325 is a 3-hyperperfect number.
327 and its double and triple together contain every digit from 1-9 exactly once.
330 = ₁₁C₄.
333 is the number of 7-hexes.
335 is the number of degree 12 irreducible polynomials over GF(2).
336 = ₈P₃.
337 is a permutable prime.
341 is the smallest pseudoprime in base 2.
342 = 666 in base 7.
343 = 7³.
350 is the Stirling number of the second kind S(7,4).
351 is the smallest number n where n, n+1, and n+2 are all products of 4 or more primes.
353 is the smallest number whose 4^th power can be written as the sum of 4 4^th powers.
354 is the sum of the first 4 4^th powers.
355 is the number of labeled topologies with 4 elements.
360 is the number of degrees in a circle.
364 = ₁₄C₃.
365 is the smallest number that can be written as a sum of consecutive squares in more than 1 way.
367 is the largest number whose square has strictly increasing digits.
369 is the number of octominoes.
370 = 3³ + 7³ + 0³.
371 = 3³ + 7³ + 1³.
373 is a permutable prime.
374 is the smallest number that can be written as the sum of 3 squares in 8 ways.
376 is automorphic.
377 is the 14^th Fibonacci number.
381 is a Karmekar number in base 2.
383 is the number of Hamiltonian graphs with 7 vertices.
384 = 8!!.
385 is the number of partitions of 18.
392 is a Karmekar number in base 5.
400 = 1111 in base 7.
401 is the number of connected planar Eulerian graphs with 9 vertices.
407 = 4³ + 0³ + 7³.
420 is the smallest number divisible by 1 through 7.
428 has the property that its square is the concatenation of two consecutive numbers.
429 is the 7^th Catalan number.
432 = (4) (3)³ (2)².
438 = 666 in base 8.
441 is the smallest square which is the sum of 6 consecutive cubes.
442 is the number of planar partitions of 13.
444 is the largest known n for which there is a unique integer solution to a₁+...+a_n=(a₁)...(a_n).
446 is the smallest number that can be written as the sum of 3 distinct squares in 8 ways.
448 is the number of 10-iamonds.
450 = (5+4)(5+5)(5+0).
454 is the largest number known that cannot be written as a sum of 7 or fewer cubes.
455 = ₁₅C₃.
456 is the number of tournaments with 7 vertices.
461 = 444 + 6 + 11.
462 = ₁₁C₅.
465 is a Karmekar number in base 2.
468 = 3333 in base 5.
469 is the largest known value of n for which n!-1 is prime.
471 is the smallest number with the property that its first 4 multiples contain the digit 4.
480 is the smallest number which can be written as the differenc of two squares in 8 ways.
483 is the last 3-digit string in the decimal expansion of pi.
484 is a palindromic square number.
487 is the number of Hadamard matrices of order 28.
490 is the number of partitions of 19.
495 is the Kaprekar constant for 3-digit numbers.
496 is the 3^rd perfect number.
497 is the number of graphs with 8 edges.
499 is the smallest number with the property that its first 12 multiples contain the digit 9.
501 is the number of partitions of 5 items into ordered lists.
504 = ₉P₃.
505 = ₁₀C₅ + ₁₀C₀ + ₁₀C₅.
510 is the number of binary rooted trees with 14 vertices.
511 = 11111111 in base 2.
512 is the cube of the sum of its digits.
518 = 5¹ + 1² + 8³.
521 is the 13^th Lucas number.
527 is the smallest number n for which there do not exist 4 smaller numbers a₁ through a₄ so that a₁! a₂! a₃! a₄! n! is square.
528 is the sum of its proper divisors that contain the digit 6.
531 is the smallest number with the property that its first 4 multiples contain the digit 1.
538 is the 10^th meandric number.
540 is divisible by its reverse.
541 is the number of orderings of 5 objects with ties allowed.
546 = 666 in base 9.
551 is the number of trees with 12 vertices.
554 is the number of self-dual planar graphs with 20 edges.
555 is a repdigit.
560 = ₁₆C₃.
561 is the smallest Carmichael number.
563 is the largest known Wilson prime.
567 has the property that it and its square together use the digits 1-9 once.
568 is the smallest number whose 7^th power can be written as the sum of 7 7^th powers.
572 is the smallest number which has equal numbers of every digit in bases 2 and 3.
573 has the property that its square is the concatenation of two consecutive numbers.
575 is a plaindrome that is one less than a square.
576 is the number of 4 x 4 Latin squares.
582 is the number of antisymmetric relations on a 5 element set.
585 = 1111 in base 8.
594 = 1⁵ + 2⁹ + 3⁴.
595 is a palindromic triangular number.
598 = 5¹ + 9² + 8³.
607 is the exponent of a Mersenne prime.
610 is the 15^th Fibonacci number.
614 is the smallest number that can be written as the sum of 3 squares in 9 ways.
619 is a strobogrammatic prime.
620 is the number of sided 7-hexes.
624 is the smallest number with the property that its first 5 multiples contain the digit 2.
625 is automorphic.
627 is the number of partitions of 20.
630 is the number of degree 13 irreducible polynomials over GF(2).
637 = 777 in base 9.
641 is the smallest prime factor of 2²⁵+1.
642 is the smallest number with the property that its first 6 multiples contain the digit 2.
645 is the largest n for which 1+2+3+...+n = 1²+2²+3²+...+k² for some k.
646 is the number of connected planar graphs with 7 vertices.
650 is the sum of the first 12 squares.
651 is an nonagonal pentagonal number.
652 has the property that e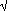⁶⁵² is within 10^-9 of an integer.
660 is the order of a non-cyclic simple group.
666 is a palindromic triangular number.
672 is multiply perfect.
676 is the smallest palindromic square number whose square root is not palindromic.
679 is the smallest number with multiplicative persistence 5.
680 is the smallest tetrahedral number that is also the sum of 2 tetrahedral numbers.
682 = ₁₁C₆ + ₁₁C₈ + ₁₁C₂.
688 has a factorization using the same digits as itself.
689 is the smallest number that can be written as the sum of 3 distinct squares in 9 ways.
697 is a 12-hyperperfect number.
703 is a Kaprekar number.
704 is the number of sided octominoes.
709 is the number of connected planar graphs with 9 edges.
710 is the number of connected graphs with 9 edges.
714 is the smallest number which has equal numbers of every digit in bases 2 and 5.
715 = ₁₃C₄.
718 is the number of unlabeled topologies with 6 elements.
719 is the number of rooted trees with 10 vertices.
720 = 6!
721 is the smallest number which can be written as the difference of two cubes in 2 ways.
727 has the property that its square is the concatenation of two consecutive numbers.
728 is the smallest number n where n and n+1 are both products of 5 or more primes.
729 = 3⁶.
730 is the number of connected bipartite graphs with 9 vertices.
731 is the number of planar partitions of 14.
732 = 1⁷ + 2⁶ + 3⁵ + 4⁴ + 5³ + 6² + 7¹.
733 = 7 + 3! + (3!)!.
735 is the smallest number that is the concatenation of its distinct prime factors.
742 is the smallest number that is one more than triple its reverse.
743 is the number of independent sets of the graph of the 4 dimensional cube.
746 = 1⁷ + 2⁴ + 3⁶.
750 is the Stirling number of the second kind S(10,8).
757 is the smallest number whose reciprocal has a period of 27.
762 is the first decimal digit of pi where a digit occurs four times in a row.
764 is the number of 8x8 symmetric permutation matrices.
765 is a Karmekar number in base 2.
767 is the largest n so that n² = _mC₀ + _mC₁ + _mC₂ + _mC₃ has a solution.
777 is a repdigit in bases 6 and 10.
780 = (5+7)(5+8)(5+0).
781 = 11111 in base 5.
784 is the sum of the first 7 cubes.
787 is a palindromic prime.
791 is the smallest number n where either it or its neighbors are divisible by the numbers from 1 to 12.
792 is the number of partitions of 21.
793 is one less than twice its reverse.
794 is the sum of the first 3 6^th powers.
797 is the number of functional digraphs on 9 vertices.
800 = 2222 in base 7.
802 is the number of isomers of C₁₃H₂₈.
810 is divisible by its reverse.
816 = ₁₈C₃.
820 = 1111 in base 9.
822 is the number of planar graphs with 7 vertices.
835 is the 9^th Motzkin number.
836 is a non-palindrome with a palindromic square.
840 is the smallest number divisble by 1 through 8.
841 is a square that is also the sum of two consecutive squares.
843 is the 14^th Lucas number.
846 has the property that its square is the concatenation of two consecutive numbers.
853 is the number of connected graphs with 7 vertices.
854 has the property that it and its square together use the digits 1-9 once.
855 is the smallest number which is the sum of 5 consecutive squares or 2 consecutive cubes.
858 is the smallest palindrome with 4 different prime factors.
866 is the number of sided 10-iamonds.
873 = 1! + 2! + 3! + 4! + 5! + 6!
877 is the 7^th Bell number.
880 is the number of 4 x 4 magic squares.
888 has a cube that whose digits each occur 3 times.
889 is a Karmekar number in base 2.
899 is the product of twin primes.
900 is a square whose digits are non-increasing.
912 has exactly the same digits in 3 different bases.
913 has exactly the same digits in 3 different bases.
914 is the number of binary rooted trees with 15 vertices.
919 is a permutable prime.
924 is the 6^th central binomial coefficient.
929 is a palindromic prime.
941 is the smallest number which is the reverse of the sum of its proper substrings.
945 is the smallest odd abundant number.
951 is the number of functions from 8 unlabeled points to themselves.
952 = 9³ + 5³ + 2³ + (9)(5)(2).
961 is a square whose digits can be rotated to give another square.
966 is the Stirling number of the second kind S(8,3).
969 is a tetrahedral palindrome.
976 has a square formed by inserting a block of digits inside itself.
979 is the sum of the first 5 4^th powers.
981 is the smallest number that has 5 different partitions into 3 parts with the same product.
986 = 1⁹ + 2⁸ + 3⁶.
987 is the 16^th Fibonacci number.
990 = ₁₁P₃.
991 is a permutable prime.
992 is the number of differential structures on the 11-sphere.
993 is the smallest number with the property that its first 15 multiples contain the digit 9.
994 is the smallest number with the property that its first 18 multiples contain the digit 9.
995 has a square formed by inserting a block of digits inside itself.
996 has a square formed by inserting a block of digits inside itself.
997 is the smallest number with the property that its first 37 multiples contain the digit 9.
998 is the smallest number with the property that its first 55 multiples contain the digit 9.
999 is a Kaprekar number.
1000 = 10³.
1001 is the smallest palindromic product of 3 consecutive primes.
1002 is the number of partitions of 22.
1006 has a cube that is a concatenation of other cubes.
1021 is the largest prime p known with the property that 1 + (2)(3)(5)(7)(11)...(p) is prime.
1023 is the smallest number with 4 different digits.
1024 is the smallest number with 11 divisors.
1025 is the smallest number that can be written as the sum of a square and a cube in 4 ways.
1031 is the largest length of a repunit that is known to be prime.
1033 = 8¹ + 8⁰ + 8³ + 8³.
1036 = 4444 in base 6.
1044 is the number of graphs with 7 vertices.
1050 is the Stirling number of the second kind S(8,5).
1052 has the property that placing the last digit first gives 1 more than twice it.
1056 is the area of the smallest non-square rectangle that can be tiled with integer-sided squares.
1067 has exactly the same digits in 3 different bases.
1078 is the number of lattices on 9 unlabeled nodes.
1079 is the smallest number n where either it or its neighbors are divisible by the numbers from 1 to 15.
1080 is the smallest number with 18 divisors.
1089 is one ninth of its reverse.
1092 is the order of a non-cyclic simple group.
1093 is the smallest Wieferich prime.
1098 = 11 + 0 + 999 + 88.
1099 = 1 + 0 + 999 + 99.
1105 is the smallest number that can be written as the sum of 2 squares in 4 ways.
1111 is a repdigit.
1116 is the number of polyabloes with 8 half squares.
1122 = ₃₃C₁ + ₃₃C₁ + ₃₃C₂ + ₃₃C₂.
1139 has the property that placing the last digit first gives 1 more than 8 times it.
1140 is the smallest number whose divisors contain every digit at least three times.
1141 is the smallest number whose 6^th power can be written as the sum of 7 6^th powers.
1148 is the number of ways to fold 9 stamps.
1153 is the smallest number with the property that its first 3 multiples contain the digit 3.
1155 is the product of 4 consecutive primes.
1156 is a square whose digits are non-decreasing.
1161 is the number of degree 14 irreducible polynomials over GF(2).
1167 is the smallest number whose 8^th power can be written as the sum of 9 8^th powers.
1170 = 2222 in base 8.
1183 is the smallest number with the property that its first 4 multiples contain the digit 3.
1184 is amicable.
1185 = 11 + 1111 + 8 + 55.
1186 is the number of 11-iamonds.
1187 = 111 + 111 + 888 + 77.
1193 and its reverse are prime, even if we append or prepend a 3 or 9.
1197 is the smallest number that contains as substrings the maximal prime powers that divide it.
1200 = 3333 in base 7.
1206 has a factorization using the same digits as itself.
1210 is amicable.
1215 is the smallest number n where n and n+1 are both products of 6 or more primes.
1224 is the smallest number that can be written as the sum of 4 cubes in 3 ways.
1225 is triangular, square and hexagonal.
1233 = 12² + 33².
1234 is the smallest 4-digit number with different digits.
1243 is the number of essentially different ways to dissect a 18-gon into 8 quadrilaterals.
1248 is the smallest number with the property that its first 6 multiples contain the digit 4.
1249 is the number of simplicial polyhedra with 11 vertices.
1255 is the number of partitions of 23.
1260 is the smallest number with 36 divisors.
1276 = 1111 + 22 + 77 + 66.
1278 = 1111 + 2 + 77 + 88.
1279 is the exponent of a Mersenne prime.
1285 is the number of 9-ominoes.
1287 = ₁₃C₅.
1294 is the number of 4 dimensional polytopes with 8 vertices.
1295 = 5555 in base 6.
1296 is the number of labeled trees with 6 vertices.
1300 is the sum of the first 4 5^th powers.
1301 is the number of trees with 13 vertices.
1306 = 1¹ + 3² + 0³ + 6⁴.
1320 = ₁₂P₃.
1330 = ₂₁C₃.
1331 is a cube containing only odd digits.
1364 is the 15^th Lucas number.
1365 = ₁₅C₄.
1366 = 1 + 33 + 666 + 666.
1369 is a square whose digits are non-decreasing.
1370 = 1² + 37² + 0².
1371 = 1² + 37² + 1².
1376 is the smallest number with the property that it and its neighbors are cubeful.
1385 is the 8^th Euler number.
1395 is a vampire number.
1405 is the sum of consecutive squares in 2 ways.
1429 is the smallest number whose square has the first 3 digits the same as the next 3 digits.
1430 is the 8^th Catalan number.
1435 is a vampire number.
1444 is a square whose digits are non-decreasing.
1448 is the number of 8-hexes.
1453 = 1111 + 4 + 5 + 333.
1454 = 11 + 444 + 555 + 444.
1455 is the number of subgroups of the symmetric group on 6 symbols.
1458 is the maximum determinant of a 11 x 11 matrix of 0's and 1's.
1459 = 11 + 444 + 5 + 999.
1467 has the property that e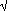¹⁴⁶⁷ is within 10^-8 of an integer.
1476 is the number of graphs with 9 edges.
1494 is the sum of its proper divisors that contain the digit 4.
1500 = (5+1)(5+5)(5+0)(5+0).
1503 has a factorization using the same digits as itself.
1506 is the sum of its proper divisors that contain the digit 5.
1518 is the sum of its proper divisors that contain the digit 5.
1521 is the smallest number that can be written as the sum of 4 distinct cubes in 3 ways.
1530 is a vampire number.
1533 is a Karmekar number in base 2.
1537 has its largest proper divisor as a substring.
1540 is both triangular and tetrahedal.
1543 = 1111 + 55 + 44 + 333.
1555 = 11111 in base 6.
1562 = 22222 in base 5.
1563 is the smallest number with the property that its first 4 multiples contain the digit 6.
1575 is the number of partitions of 24.
1595 is the smallest quasi-Carmichael number in base 2.
1597 is the 17^th Fibonacci number.
1600 = 4444 in base 7.
1606 is the number of strongly connected digraphs with 4 vertices.
1624 is the Stirling number of the first kind s(7,3).
1632 is the smallest number with the property that its first 5 multiples contain the digit 6.
1634 = 1⁴ + 6⁴ + 3⁴ + 4⁴.
1638 is a harmonic divisor number.
1639 is the number of binary rooted trees with 16 vertices.
1640 = 2222 in base 9.
1650 has exactly the same digits in 3 different bases.
1676 = 1¹ + 6² + 7³ + 6⁴.
1680 is the smallest number with 40 divisors.
1681 is a square and each of its two 2-digit parts is square.
1689 is the smallest composite number all of whose divisors (except 1) contain the digit 9.
1701 is the Stirling number of the second kind S(8,4).
1705 is the smallest quasi-Carmichael number in base 4.
1715 = (1) (7)³ (1) (5).
1716 = ₁₃C₆.
1722 is a Giuga number.
1728 = 12³.
1729 is the smallest number which can be written as the sum of 2 cubes in 2 ways.
1730 is the sum of consecutive squares in 2 ways.
1734 is the sum of its proper divisors that contain the digit 8.
1755 = 3333 in base 8.
1763 is the product of twin primes.
1764 is the Stirling number of the first kind s(7,2).
1771 is a tetrahedral palindrome.
1782 is the smallest number n that is 3 times the sum of all the 2-digit numbers that can be made using the digits of n.
1785 is a Karmekar number in base 2.
1789 is the smallest number with the property that its first 4 multiples contain the digit 7.
1820 = ₁₆C₄.
1827 is a vampire number.
1828 is the 11^th meandric number.
1842 is the number of rooted trees with 11 vertices.
1849 is the smallest composite number all of whose divisors (except 1) contain the digit 4.
1854 is the number of derangements of 7 items.
1858 is the number of isomers of C₁₄H₃₀.
1890 is the smallest number whose divisors contain every digit at least four times.
1905 is a Karmekar number in base 2.
1908 is the number of self-dual planar graphs with 22 edges.
1915 is the number of semigroups of order 5.
1947 is the number of planar partitions of 16.
1953 is a Karmekar number in base 2.
1958 is the number of partitions of 25.
1960 is the Stirling number of the first kind s(8,5).
2000 = 5555 in base 7.

Продолжение списка интересных чисел