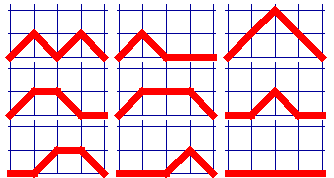
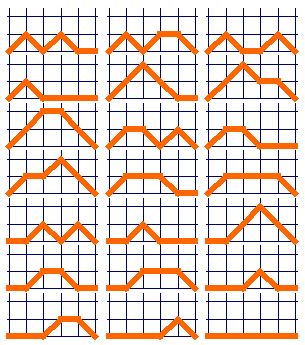
Если мы введем количество стопок книг равное пяти, а количество книг в стопках соответственно 3, 4, 8, 5 и 6, то увидим на экране эту расстановку.

1 … 3 ***
2 … 4 ****
3 … 8 ********
4 … 5 *****
5 … 6 ******
ДЛЯ ПРОДОЛЖЕНИЯ - 1, ДЛЯ ВЫХОДА - 0 ?

Если запустим процесс, нажав “1”, то увидим на экране, что количество книг в стопках уменьшилось на 1 и добавилась новая стопка с пятью книгами. Нажимая «1» и «Enter» мы увидим процесс, протекающий по заданному нами закону и, если повезет, найдем закономерность. C помощью программы случайно удалось найти самое примитивное устойчивое колебание для случая из двух книг - то две стопки по одной книге, то одна с двумя. А сама модель еще ждет своих Коперников-Лобачевских.

Семинар

Все видели выкладывание шаров в биллиарде треугольником. Количество шаров в треугольнике порождает последовательность треугольных чисел, где номер числа соответствует количеству рядов шаров: 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, …n*(n+1)/2…причем треугольные числа еще и равны сумме чисел натурального ряда, например, 45=1+2+3+4+5+6+7+8+9. Настоящие любители сразу заметят знакомцев, например, 21 и 55 - числа Фибоначчи, 6 и 28 - совершенные числа, 36 - квадратное число, и это только в самом начале ряда. Квадратные числа - естественно квадраты чисел натурального ряда: 1, 4, 9, 25, 36, 49, 64… Числа же 1, 36, 1225, 41616, 1413721, … и треугольные и квадратные, их можно представить в виде произведения квадратов некоторых чисел. Если мы на три касающихся шара сверху положить четвертый - получим тетраэдр, три шара второго ряда можно положить на 6 шаров третьего ряда, а их, в свою очередь, на 10 шаров третьего ряда. Сумма шаров по рядам дадут последовательность, называемую тетраэдальной: 1, 4, 10, 20, 35, 56, 84, 120, … n*(n+1)*(n+2)/6… Каждое тетраэдальное число равно сумме треугольных, начиная с первого. Если шар укладывать на 4 касающихся шара, уложенных на 9 шаров и т.д., то мы получим пирамидальные числа 1, 5, 14, 30, 55, 91, 140, 204, … n*(n+1)*(2n+1)/6…Единственным тетраэдальным и пирамидальным (>1) числом является 4900. Если вам встретятся где-либо эти числа, вы теперь отнесетесь ним как к добрым знакомым.

Числовые последовательности попадаются довольно забавные. Например, выберите число и найдите сумму квадратов его цифр, потом проделайте это с полученной суммой ещё и ещё раз. Кстати, прекрасное средство от бессонницы. Придём ли мы к чему-нибудь? Как зависит то, к чему мы придем от начального числа? Задача просто идеальная для начинающих программистов, для тех, кто изучает Бейсик или Паскаль. Основная проблема - выделить цифры числа. Здесь можно посоветовать два пути. Первый - делить на 10 с последующим отбрасыванием дробной части округлением, второй - преобразовать число в строковую переменную, выделять по одной цифре и снова преобразовать их в числа. Программа настолько проста, что приводить ее не будем. Я узнал эту задачу лет за 10 до появления ПК и заинтересовавшимся могу посоветовать записывать процесс на бумаге, тогда вы быстро выявите несколько «зацикливаний». Попробуйте - не пожалеете! Теперь та же операция, но с суммой кубов цифр числа. Удивительно, но если начальное число кратно трём, то мы всегда будем кончать повтором одного и того же числа (какого?). А если не кратно трём? Запишите как домашнее задание.

Ещё одна последовательность: первый член произвольное нечётное число, отличное от единицы. Следующее за числом р равно р/2, если р чётно, 3*р+1, если р нечётно. Последовательность заканчивается, если встретится значение равное единице. Всегда ли последовательность достигает 1? Как это зависит от начального числа? Хорошее упражнение для Бейсика. Сопутствующий вопрос: как попроще выяснить четность числа? И ещё одна, «последняя интересная» последовательность, «вкусная» для Бейсика. Напишите четырёхзначное число. Теперь выпишем цифры этого числа в порядке возрастания и вычтем полученное число из начального. Разница будет вторым членом последовательности. Продолжая такую мудрёную операцию, вскоре заметим, что мы «циклим» на числе 6174 независимо от начального числа и ещё заметим, что не можем это объяснить. Это число называется постоянной Капрекара в честь индийского математика, открывшего его. С его же именем связан замечательный класс чисел, открытый Капрекаром в 1949 году и названный им самопорожденными числами. Если к любому числу (генератору) прибавить сумму его цифр, то получим новое число, порожденное первым. Возникает множество вопросов: может ли число иметь более одного генератора? Как найти числа, не имеющие генератора? Такие числа и называются самопорожденными.

Попутный вопрос, не имеющий отношения к последовательностям, для разминки - сколько существует четырёхзначных чисел, в записи которых нет повторяющихся цифр? Не так уж много… Услышав эту задачу (задавалась на какой-то олимпиаде для школьников) я с нетерпением дождался «встречи» с Бейсиком, тогда еще на СМ-4, чтобы убедиться, что таких чисел неожиданно мало. Совсем нетрудно выделять цифры и сравнивать их, но попробовать обязательно стоит, причем интересно не только узнать количество чисел с разными цифрами, но и выводить их «по ходу дела» на экран для обозрения.

На сколько кусков можно разрезать круглый блин, проводя n разрезов ножом? (Разрезы прямые и не проходят через одну точку). Порисуйте и поразмышляйте, и вы быстро найдете: 2, 4, 7, 11 … и, подумав еще, формулу n*(n-1)/2 +1. Интересная последовательность, (1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, ...), названная по имени Каталана Юджина Чарльза (1814 - 1894), встречается в самых разных ситуациях. Например, еще Леонард Эйлер задался вопросом - сколькими способами можно разделить выпуклый многоугольник на треугольники с помощью непересекающихся диагоналей? Квадрат можно разделить двумя способами, а пятиугольник - четырнадцатью.

Число маршрутов ладьи из левого нижнего угла доски n*n в правый верхний (не заходя в зону выше и левее главной диагонали) тоже определяется числами Каталана.

Похожа на числа Каталана последовательность Белла (1, 1,  2,  5,  15,   52,  203,  877,  4140,  21147,  115975,  678570,   4213597,  ...), показывающая, например, количество вариантов, которыми могут быть разгруппированы n элементов. Например, набор {1,   2,  3} может быть разделен следующими способами: { {1},  {2},  {3}}  { {1, 2},  {3}}  { {1, 3},  {2}}  { {1}, {2, 3}}  { {1, 2, 3}}. Что соответствует четвертому числу Белла. А еще числа Белла показывают число вариантов рифм в n строках. Для 1 строки - 1 вариант, для двух - два (aa и ab), для трех - 5 вариантов (aaa, aab, aba, abb, abc), для четырех - 15 вариантов:
aaaa, aaab, aaba, abaa, abbb,
aabb, abba, abab, aabc, abac,
abca, abbc, abcb, abcc, abcd

Какой схеме соответствует фрагмент песни Высоцкого:

«Потом еще была уха,
И заливные потроха.
Потом поймали жениха
И долго били»?

А этот детский стишок:

«Не идется и не едется,
Потому, что гололедица.
Но зато отлично падается,
Почему ж никто не радуется?»

Если вы уверены, что вариант abcd не встречается, то напрасно, вот куплет из популярной веселой туристической песни:

«Муха тоже вертолет,
Только маленький совсем.
Я хотел его поймать -
Улетел пернатый друг»

Попробуйте вспомнить примеры для других схем - увлекательное занятие..

Костяшка домино состоит из двух квадратиков, тримино - из трех. Тримино может существовать в двух вариантах - в линию и уголком. А уж пять фигурок тетрамино знакомы каждому, ибо они сыплются в не имеющем конкурентов по популярности Тетрисе. Двенадцать плиток пентамино тоже необычайно популярны, читатели постарше помнят, что в «Науке и жизни» 70-х был постоянный раздел, посвященный составлению фигурок из набора пентамино. А сколько существует гексамино и гептамино? Сколькими вариантами можно сложить цепочки из n треугольников? А шестиугольников?

Числа Люка (1, 3, 4, 7, 11, 18, 29, 47, 76, 123,…) похожи на числа Фибоначчи, но начинаются не с двух единиц, а с единицы и тройки, далее идут суммы двух предыдущих чисел. Интересно, что отношение двух соседних чисел Люка также стремится к золотому сечению: 18/11 = 1.6363.. 29/18 = 1.6111.. 47/29 = 1.6206.. 76/47 = 1.6170.. 123/76 = 1.6184.. постепенно приближаясь к магическому значению 1.6180339887. Об этих и других последовательностях можно поподробнее посмотреть на страничке математика Роберта М. Дикко (Robert M. Dickau ) с иллюстрациями и строгими формулами. Еще есть числа Деланне (1, 13, 63,…), показывающие количество вариантов перехода шахматного короля поля n*n по диагонали с учетом возможного движения по диагонали, и числа Мотцкина (Motzkin Numbers - 1, 2, 4, 9, 21,…), показывающие количество вариантов перехода шахматного короля поля n*n из нижнего левого угла в нижний правый угол с учетом возможного движения по диагонали.

Числа Стирлинга показывают количество вариантов разбиения n элементов на k групп. Например, четыре элемента на две группы можно разбить следующими способами: {{1,3,2},{4}}  {{1,2,3},{4}}   {{1,4,2},{3}}  {{1,2,4},{3}}  {{1,2},{3,4}}   {{1,4,3},{2}}   {{1,3,4},{2}}  {{1,3},{2,4}}  {{1,4},{2,3}}  {{1},{2,4,3}}   {{1},{2,3,4}}  Всего 11 вариантов, то есть s(4, 2) = 11. А множество из трех чисел {1, 2, 3} на три части можно разбить единственным образом: {{1}, {2}, {3}}, на две части - тремя способами: {{1, 2}, {3}} {{1, 3}, {2}} {{1}, {2, 3}}, И одна часть - опять единственным образом: {{1, 2, 3}}.

Заповедник последовательностей

Наш небольшой обзор не претендует на энциклопедическую полноту, но если вдруг вам на работе или при развлечениях встретится числовая последовательность, вы будете вооружены и, возможно, разглядите в ней знакомую, во всяком случае не растеряетесь. Но, все же, могут встретиться и совсем незнакомые, как же подступиться к ним, подобрать формулу, найти следующее число, узнать об аналогичных процессах? Еще лет десять назад я с завистью прочитал у М. Гарднера («Путешествие во времени», М., Мир 1990), что существует «Справочник по целочисленным последовательностям». Составитель его Н. Слоун, сотрудник фирмы Bell Laboratories, собрал и упорядочил более 2300 целочисленных последовательностей, расположив их в порядке возрастания первых, вторых и т.д. членов. Исследователю, встретившему загадочную целочисленную последовательность, теперь не нужно затрачивать часы на поиск производящей ее формулы - достаточно просто заглянуть в справочник Слоуна. С высокой вероятностью он найдет там свою последовательность вместе со списком рекомендуемой литературы, по которой можно установить природу интересующего его «зверя». Оставалось только найти этот справочник. Представьте мое удивление, когда, прогуливаясь по математическим страничкам, я попадаю к Брайану Хейсу (Brian Hayes ), ведущему рубрики в журнале Computing Science. В статье (№1 аж за 1996 год - для Интернета прошла целая эпоха,  http://www.amsci.org/amsci/issues/comsci96/compsci96-01.html ) он пишет, что Плоуфф (Plouffe), математик из Университета Саймона Фрасера в Британской Колумбии несколько лет назад вызвался помочь Слоуну (тому самому!) пересмотреть и расширить «Справочник». Результатом их сотрудничества стала «Энциклопедия Последовательностей Целых Чисел», содержащая более 5400 (!) последовательностей. И, самое главное, эта Энциклопедия доступна в Сети, и не просто доступна, а автоматически обрабатывает присланную вами последовательность, определяет ее происхождение и параметры, дает ссылки на похожие работы и т.д., то есть выполняет всю черновую работу, оставляя вам только творческую часть. Надо отправить по адресу sequences@research.att.com   (запоминайте) одно единственное слово: «lookup» и перечислить через пробелы первые известные члены.

Конечно же, не терпится испытать Энциклопедию. Как назло под рукой ничего подходящего не оказалось, пришлось на ходу придумывать последовательность - первая же, взятая с потолка формула n*(n+3)/2 порождала числа 2,   5,  9,  14,  20,  27,  35,  44, которые и были написаны после lookup и отправлены. Прошло минуты две-три, как вдруг летучая мышь в трее замахала крыльями (просто невероятно - письмо из соседней организации идет не менее часа, а тут с другого конца планеты…), возвещая о потрясающем ответе.

Во-первых, неизвестный ответчик-энциклопедист сообщил, что последовательность ему известна под номером N0522 и выдал первые 50 членов:0,2,5,9,14,20,27,35,44,54,65,77,90,104,
119,135,152,170,189,209,230,252,275,299,324,350,377,
405,434,464,495,527,560,594,629,665,702,740,779,819
,860,902,945,989,1034,1080,1127,1175,1224,1274,1325,1377,1430

Во-вторых, была указана формула n*(n+3)/2, та самая, которой я хотел испытать автоответчик.

В-третьих, сообщалось, что Роберт Г. Вильсон установил, что для n>1 эта последовательность показывает максимальное количество кусков, на которые можно разрезать плоское кольцо, проводя n разрезов! Проверьте - работает!!!

В четвертых, Антреас Хатзиполакис установил, что при n>=3 это количество диагоналей, которые можно провести в n-угольнике. Убедитесь - это так!!!
Далее еще шли около десятка ссылок на разные работы {например, члены этого ряда являются биноминальными коэффициентами многочлена A(x) = x*(2-x)/(1-x)^3, но я не проверял}, но совсем меня «добило» сообщение о том, что члены ряда на единицу меньше треугольных чисел, знакомых вдоль и поперек с детства. Как можно было сразу этого не заметить, ума не приложу.

Не успевая поверить в такого волшебного «подсказчика» чуть меняю формулу, задаю зависимость n*(n+5)/2, порождающую числа 3, 7, 12, 18, 25, 33, … и отправляю письмо. Через несколько минут пришел ответ, с удивительными сообщениями:

• Первые 50 членов нашей последовательности - 1,3,7,12,18,25,33,42,52,63,75,88,102,117,133,150,168,
  187,207,228,250,273,297,322,348,375,403,
  432,462,493,525,558,592,627,663, 700,738,
  777,817,858,900,943,987,1032,1078

• Эту последовательность описывает формула (1+x^2-x^3)/(1-x)^3.

• Эта последовательность - треугольные числа, у каждого из которых вычли 3

• Нашли и мою формулу: n*(n+5)/2.

• И еще формула: G.f.(x)=x(3-2x)/(1-x)^3, с предупреждением, что она для ряда, сдвинутого на три позиции.
  
  

Сотрудник, с которым я делился восторгом, предложил послать последовательность из случайных чисел. Несчастный робот через пару минут ответил, что в его коллекции нет этой последовательности, и что он будет нам очень признателен, если мы пришлем ему описание процесса, в котором мы получили эту последовательность для включения ее в банк последовательностей, он заранее нас благодарит, подробности просит смотреть на .
Небольшое отступление. Я написал «несчастный робот» не потому, что в это время в Америке была глубокая ночь, а потому, что я испытываю чувство, если не вины, но некоторого сожаления, когда приходится загружать компьютер заведомо бестолковыми задачами. Излюбленная тема фантастов - можно ли испытывать чувство вины перед роботом? (Например, ). Все понимаем, что это железяка с осколками кремния и мотком проводов, но - жалко. Впрочем, это, должно быть, излишняя сентиментальность.

Брайан Хейс пишет также, что, рассматривая «Последовательность Последовательностей», как он назвал Энциклопедию целых чисел, он испытал приятные мгновения. Можно встретить совсем неожиданные примеры. Например, имеется последовательность, обозначенная M2675, которая начинается 1, 3, 7, 19, 53, 149, 419 ...; каждый элемент которой - число устойчивых башен, которые могут быть построены из n блоков конструктора Lego. 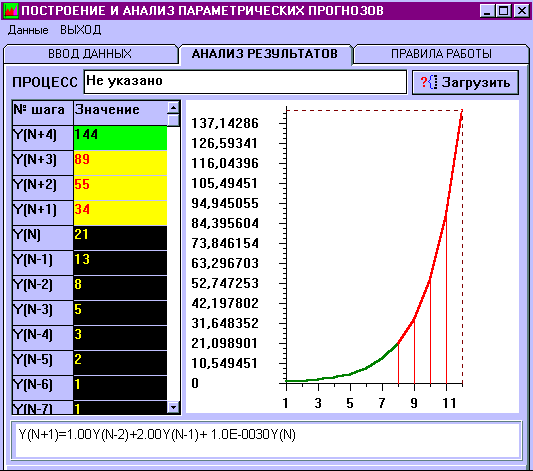А под номером M1041, показаны числа 1, 2, 4, 7, 11, 16, 22 ..., - те самые куски блина, на который разрезали мы его в начале статьи.
Есть и более экзотические ряды вроде М4780, который начинается 1, 11, 21, 1211, 111221 ...., попробуйте отгадать закономерность. Есть и просто шутки типа M4961: 1, 15, 29, 12, 26, 12, 26, 9, 23, 7, 21 .... с описанием - " Даты в двухнедельных интервалах с 1 января. " Конечные последовательности (с известным числом членов, как, например, события со Страшилой в эпиграфе), как предполагается, не включены, но некоторые вкрались в Последовательность последовательностей. Например, M3296, начинающаяся 1, 4, 7, 9, 11, 12, 14, 16 ... и дается намек: «Это заканчивается номером 92 в природе, но доходит до, по крайней мере, 106 в лаборатории. (По моему ИМХО это атомные веса элементов, уже вроде и 114 синтезировали. Е.С.)

Запрещены включения в Энциклопедию представленные некоторыми чудаками такие, например, числа, как расписание электричек.
Страничка Н. Слоуна с Энциклопедией и адресами для запросов расположена на Center for Experimental and Constructive Mathematics  и еще Sloane's home page Но считать, что Энциклопедия Последовательностей наша единственная опора в «разборках» с рядами чисел не совсем правильно. Мой знакомый по переписке, любитель занимательной математики Сергей Донцов разработал программу, прогнозирующую следующее значение ряда чисел. В программе конкурируют более 1000 вариантов уравнений полиномов, позволяя получить интересные результаты. Вот как идеально программа по введенным восьми числам выдала четыре следующих числа Фибоначчи.

Если же «подсунуть» программе ту же последовательность, которой мы тестировали «Энциклопедию», то она прогнозирует несколько другие значения следующих четырех чисел. Причем график функции имеет гладкий вид, что подтверждает «право на существование» спрогнозируемого результата, возможно, он и встретится в каком-либо процессе.
Скачать программу для научной работы или чтобы просто поиграть c числами можно с здесь, Там же есть и удивительная программа того же автора, которая распознает изображения с помощью нейросети Кохонена. Для любителей математики совершенно бесплатно.

Обещанное

Теперь терпеливый читатель, заинтригованный заголовком и вынужденный читать все это в ожидании обещанных кроликов, будет вознагражден. В другой интересной статье того же Брайана Хейса «Числа Вибоначчи» (http://www.amsci.org/amsci/issues/comsci99/compsci1999-07.html ) автор проводит интересные «опыты» с числами Фибоначчи. Во-первых, он предлагает в формуле ряда Фибоначчи f (n) = f(n - 2) + f (n - 1) знак суммы иногда (случайным образом) менять на минус. Новую сущность автор предлагает назвать рядом Вибоначчи, так как он «вибрирует» случайным образом. (Правильнее было бы «Виброначчи»). Запустив датчик случайных чисел, например, в виде монетки, можно породить несколько вариантов Вибоначчи, например, такие: 1, 1, 0, 1, - 1, 2, - 3, - 1, - 2, 1, - 3, 4, 1, 3, 4, 7, 11 1, 1, 2, - 1, 3, 2, 1, 1, 0, 1, - 1, 0, - 1, 1, - 2, - 1, - 1 1, 1, 2, - 1, 3, 2, 1, 3, - 2, 1, - 3, - 2, - 5, 3, - 8, - 5, - 13 1, 1, 0, 1, - 1, 0, - 1, 1, - 2, 3, 1, 2, - 1, 3, - 4, 7, - 11 1, 1, 0, 1, 1, 2, 3, 5, - 2, 7, 5, 12, - 7, 19, - 26, 45, 19 Рассмотрев свойства чисел Вибоначчи по аналогии со свойствами Фибоначчи (подробнее о свойствах чисел Фибоначчи, в том числе и о применении их в игре на бирже, можно прочитать на здесь), автор выводит интересные аналогии и самая интересная из них - модель из жизни кроликов.

Дело в том, что по иронии судьбы Леонардо Фибоначчи, внесший существенный вклад в развитие математики, в наши дни известен потому, что живший в позапрошлом веке французский математик Эдуард Люка назвал его именем числовую последовательность, возникающую в одной довольно тривиальной задаче из «Книги об абаке», написанной Леонардо в 1202 году. Вот эта задача в том виде, как формулирует ее сам Фибоначчи. «Пара кроликов через месяц производит на свет другую пару, а потомство они дают со второго месяца после своего рождения. Итак, через месяц будет две пары, через два месяца - три пары, а через четыре месяца - пять, так как к паре, рожденной первой парой добавятся первые дети от второй пары…». Продолжая процесс (конечно, лучше карандашом на бумаге), мы и получим количество пар кроликов по месяцам: 1, 1, 2, 3, 5, 8, 13, 21, 35, 56… - эти числа и представляют ряд, названный по имени автора задачи.

И так повелось, что именно кролики остались самым наглядным пособием при объяснении закономерностей этих чисел. Поэтому Брайан Хейс снова обратился к кроликам. И не нашел ничего лучше, чтобы объяснить странное поведение чисел Вибоначчи тем, что кролики иногда поедают друг друга. Это, конечно, модель (кролики травоядные и уж никак не каннибалы), несколько не этичная, (хотя их все равно съедят хозяева, не обязательно математики), но дающая простор для анализа. Ведь поведение ряда Вибоначчи зависит от того, какого кролика съели - старого, заканчивающего плодиться, молодого, в разгаре известного процесса, или крольчонка. Порассуждайте на досуге об этом.

Брайан Хейс рассмотрел и другие модификации чисел Фибоначчи. Числа Люка мы рассмотрели выше, а вот рядом Трибоначчи предлагается назвать ряд, каждый член которого, начиная с третьего, равен сумме трех предыдущих членов 1, 1, 2, 4, 7, 13, 24, 44, 81, 149… Отношение соседних членов ряда стремится к 1.83929. Аналогично отношение членов ряда Тетрабоначчи 1, 1, 2, 4, 8, 15, 29, 108, … стремится к 1.92756 .... И далее напрашивается обобщение для чисел k-боначчи с предложением подумать, что это за ряд в предельном случае, когда каждый член равен сумме всех предыдущих? И чему будет равно тогда отношение соседних чисел ряда?

Пока думаете, еще задача, связанная с целыми числами. Двое пьют пиво. Для выяснения кому платить оба записывают любое число и сравнивают их. Тот, кто записал большее число платит за двоих, если его число отличается от другого более, чем на 1. Если же разность чисел равна 1, то платит за двоих, причем два раза подряд, тот, кто написал меньшее число. Есть ли оптимальная стратегия? Могли бы вы написать программу с выигрышной стратегией, а потом обыграть ее? И еще одна возможность выбрать, кому бежать за пивом, если нас больше двух. Все загадывают число, например, вес буфетчицы, или высота стакана, считают среднее, и у кого число дальше всех (или ближе - как договоритесь) от среднего, тот и виноват.

Теперь читатели во всеоружии запросто ответят на легкие вопросы. Сколько существует вариантов расстановок ферзей на доске n*n, при которых они не бьют друг друга? И классическая задача о рассеянной секретарше, перепутавшей письма и конверты - сколькими вариантами можно разложить n писем по конвертам? (Кстати, классный вопрос - какова вероятность, что n писем из m перепутанных это несчастье офиса случайно положит в свои конверты и они дойдут по своим адресам?) Сколькими вариантами можно расселить n туристов в m номерах гостиницы? Встретились n друзей - сколько было рукопожатий? Если у каждого человека в среднем n друзей, то сколько рукопожатий от меня до Буша-младшего? Ою этом парадоксе подробнее здесь.

На рукопожатиях, пожалуй, и закончим. Сразу все решать вовсе не обязательно - оцените красоту задач, таящих в себе числовые последовательности. А где они (последовательности) живут, благодаря усилиям двух энтузиастов, - вы теперь знаете. Многие, наверное, догадались, что ряд чисел, равных сумме всех предыдущих, хорошо известен бесконечному ряду программистов, оперирующим битами и байтами, ибо состоит он из степеней двойки: 1, 1, 2, 4, 8, 16, 32, 64,…и вопрос об отношении соседних чисел разрешается сам собой. Вот уж никак не ожидали от опытов с Фибоначчи такого завершения.