Письмо читателя Александра Высоцкого насчет статьи Кролики-каннибалы

Письмо читателя Александра Высоцкого насчет статьи "Кролики-каннибалы, четверостишия и заповедник последовательностей" в журнале Hard'n'Soft №4 2002.
Перейти к статье >>>>>>

1. Поэкспериментировав с приведенными в статье, а также в МатЭС и др., формулами для треугольных, квадратных, пятиугольных, тетраэдрических, пирамидальных и пр. фигурных чисел, вывел (не претендую на приоритет) более общие формулы:
для 1-мерных q-угольных чисел ;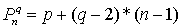
(обычная арифметическая прогрессия)

для 2-мерных q-угольных чисел ;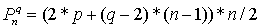

для 3-мерных q-угольных (пирамидальных) чисел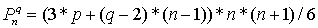

для m-мерных q-угольных чисел .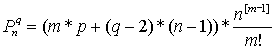

При p=1 получаются приведенные в указанных источниках формулы для треугольных и пр. чисел, при прочих – смещенные, предлагаю название “трапецеидальные”, числа.

Обозначение - n^[m]=n*(n+1)*…*(n+m-1)

Вместо доказательства предлагаю экспериментальную проверку в прилагаемой EXCEL- таблице, в ней для каждого m - 2 строки – верхняя получается суммированием, нижняя по формуле из макроса.

Исходные данные задаются: q = cells(1,1) m = cells(2,2)

Код макроса:

Dim i As Integer
Dim n As Integer
Dim m As Integer
Dim s As Integer
Sub Begin()
' Begin Макрос
' Макрос записан 24.05.02
If ActiveSheet.Name <> "Dia1" Then Exit Sub

For i = 1 To 24
Cells(i, 1).Value = 0
Next i

Randomize ' Инициализирует генератор случайных чисел.
m = 10
n = Int((m * Rnd) + 1) ' Возвращает случайное число от 1 до m.
s = 0

For i = 1 To n
Cells(i, 1).Value = Int((m * Rnd) + 1)
s = s + Cells(i, 1).Value
Next i
ChLine
Cells(22, 1).Value = m
Cells(24, 1).Value = n
Cells(23, 1).Value = s / n

End Sub

Sub RePos()
' Очередная итерация

If ActiveSheet.Name <> "Dia1" Then Exit Sub

n = Cells(24, 1).Value
s = 0

For i = 1 To n
Cells(i, 1).Value = Cells(i, 1).Value - 1
s = s + Cells(i, 1).Value
Next i

Cells(n + 1, 1).Value = n
s = s + n
n = n + 1

ChLine
Cells(24, 1).Value = n
Cells(23, 1).Value = s / n

End Sub
Sub histo()
'
' histo Макрос
' Макрос записан 24.05.02
'
Charts.Add
ActiveChart.ChartType = xlColumnClustered
ActiveChart.SetSourceData Source:=Sheets("Dia1").Range("A1:A24"), PlotBy:= xlColumns
ActiveChart.Location Where:=xlLocationAsObject, Name:="Dia1"
With ActiveChart
.HasTitle = False
.Axes(xlCategory, xlPrimary).HasTitle = False
.Axes(xlValue, xlPrimary).HasTitle = False
End With
End Sub
Sub ChLine()
'
' ChLine Макрос
' Макрос записан 24.05.02
' Удаление-перенос пустой строки
'
i = 1

While (i <= n)
If Cells(i, 1).Value = 0 Then
Cells(i, 1).Select
Selection.EntireRow.Cut
Cells(n + 1, 1).Select
Selection.EntireRow.Insert Shift:=xlDown
Cells(n + 1, 1).Value = 0
n = n - 1
Else
i = i + 1
End If
Wend
End Sub

' К статье о фигурных числах

Function Fig(n, q As Integer, m As Integer, p)

If n = 1 Then
a = p
Else
a = q - 2
End If

If m > 0 Then
a = (q - 2) * (n - 1) + p * m
End If

For i = 2 To m
a = a * (n - 2 + i) / i
Next i
Fig = a
End Function

Function Fig0(n, q As Integer)
Fig0 = q - 2
End Function
Function Fig1(n, q As Integer)
Fig1 = (n * (q - 2) + (3 - q)) / 1
End Function
Function Fig2(n, q As Integer)
Fig2 = n * (n * (q - 2) + (4 - q)) / 1 / 2
End Function
Function Fig3(n, q As Integer)
Fig3 = n * (n + 1) * (n * (q - 2) + (5 - q)) / 1 / 2 / 3
End Function
Function Fig4(n, q As Integer)
Fig4 = n * (n + 1) * (n + 2) * (n * (q - 2) + (6 - q)) / 1 / 2 / 3 / 4
End Function
Function Fig5(n, q As Integer)
Fig5 = n * (n + 1) * (n + 2) * (n + 3) * (n * (q - 2) + (7 - q)) / 1 / 2 / 3 / 4 / 5
End Function

Результат работы макросов в Excel можно скачать здесь (zip-архив 22 кб)>>>>>>

2. Для эксперимента с задачей перекладывания книг, чтобы не возиться с вводом-выводом число колонок и число книг в них получаю подпрограмму Rnd() и заношу в ячейки таблицы, при получении 0 просто строку переношу в конец, вместо звездочек – первая попавшаяся диаграмма. (Ячейку с масштабом m вывожу в диаграмму, чтобы она не прыгала).

3. В сообщении о Вашем эксперименте формула о числе диагоналей вызывает сомнения, в ней напрашивается минус.

Александр Высоцкий niiredut@i.com.ua

Мои комментарии к письму:
1 Действительно, приведенные формулы дают треугольные, квадратные, пирамидальные, тетраэдальные и так далее числа. Ранее такие обобщенные формулы мне не встречались. (Хотя это вовсе и не значит, что их кто-либо не опубликовал ранее). Название “трапецеидальные” числа довольно подходящее :)
2. Звездочки вроде нагляднее, хотя диаграммы симпатичные... но обе модели иллюстративные, к сути процесса не приближают... :(
3. Я пытался проверить - в треугольнике 0 диагоналей, в 4-х угольнике - 2 диагонали, в 5-угольнике - 5, в 6-угольнике - 9, в 7-угольнике - 14 диагоналей, что совпадает с членами ряда, дальше не проверял, но уверен, что тоже подойдет, значит формула верная...

Если есть замечания - пишите>>>>>>>
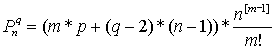