|
|
|
|
|
|
|
|
|
посетите также Клуб фанатиков числа ПИ на Арбузе На круглых дураков число "пи" не распространяется. В. Шендерович Абсолютно все знают, что такое p. Но знакомое всем со школы число возникает во многих ситуациях, не имеющим никакого отношения к окружностям. Его можно встретить в теории вероятностей, в формуле Стирлинга для вычисления факториала, в решении задач с комплексными числами и прочих неожиданных и далеких от геометрии областях математики. Английский математик Август де Морган назвал как-то p “…загадочным числом 3,14159…, которое лезет в дверь, в окно и через крышу”. Это таинственное число, связанное с одной из трех классических задач Античности - построение квадрата, площадь которого равна площади заданного круга - влечет за собой шлейф драматических исторических и курьезных занимательных фактов. В каждой книге по занимательной математике вы непременно найдете историю вычисления и уточнения значения числа p. Сначала, в древних Китае, Египте, Вавилоне и Греции для расчетов использовали дроби, например, 22/7 или 49/16. В Средние века и Эпоху Возрождения европейские, индийские и арабские математики уточнили значение p до 40 знаков после десятичной точки, а к началу Эпохи Компьютеров усилиями многих энтузиастов количество знаков было доведено до 500. Такая точность имеет чисто научный интерес (об этом ниже), для практики, в пределах Земли достаточно 11 знаков после точки. Тогда, зная, что радиус Земли равен 6400 км или 6,4*1012 миллиметров, получится, что мы, отбросив двенадцатую цифру p после точки при вычислении длины меридиана, ошибемся на несколько миллиметров. А при расчете длины Земной орбиты при вращении вокруг Солнца (как известно, R=150*106 км = 1,5*1014 мм) для такой же точности достаточно использовать p с четырнадцатью знаками после точки. Среднее расстояние от Солнца до Плутона - самой далекой планеты Солнечной системы - в 40 раз больше среднего расстояния от Земли до Солнца. Для вычисления длины орбиты Плутона с ошибкой в несколько миллиметров достаточно шестнадцати знаков p. Да что уж там мелочиться - диаметр нашей Галактики около 100.000 световых лет (1 световой год примерно равен 1013 км) или 1018 км или 1030 мм., а еще в XXVII веке были получены 34 знака p, избыточные для таких расстояний. В чем же сложность вычисления значения p? Дело в том, что оно не только иррациональное (то есть его нельзя выразить в виде дроби P/Q где P и Q целые числа), но оно еще не может быть корнем алгебраического уравнения. Число , например, иррациональное, не может быть представлено отношением целых чисел, но оно является корнем уравнения Х2-2=0, а для чисел p и е (постоянная Эйлера), нельзя указать такое алгебраическое (не дифференциальное) уравнение. Такие числа называются трансцедентными и вычисляются рассмотрением какого-либо процесса и уточняются за счет увеличения шагов рассматриваемого процесса. Самый “простой” путь - вписывать в окружность правильный многоугольник и вычислять отношение периметра многоугольника к его “радиусу”. При увеличении числа сторон это отношение будет стремиться к удвоенному p. Так, например, в 1593 году Адриан ван Ромен вычислил периметр вписанного правильного многоугольника с 1073741824 (т.е. 230) сторонами и определил 15 знаков p. В 1596 году Лудольф ван Цейлен получил 20 знаков, рассчитав вписанный многоугольник с 60*233 сторонами. Еще один путь вычислителей p - через формулы с бесконечным числом членов: p=2*(2/1*2/3*4/3*4/5*6/5*6/7*8/7)
Подобные формулы можно получить, раскладывая, например, арктангенс в ряд Маклорена, зная, что arctg(1)=p/4 (потому что tg(450)=1 - это знает даже наша кошка) или раскладывая в ряд арксинус, зная, что arcsin(0.5)=p/6 (катет, лежащий против угла в 300…). Много необычных формул и историю уточнения знаков p вы найдете на страничке http://numbers.computation.free.fr/Constants/Pi/pigeometry.html . А если вы заинтересовались программами по уточнению значения p, то посетите http://gallery.uunet.be/kurtvdb/pi.html . А теперь предлагаю всем прикоснуться к вершине достижения человеческого разума, впитавшего знания, энтузиазм и судьбы тысяч математиков-вычислителей за последние 4000 лет и, ощущая трепет, рассмотреть первые 1000 знаков числа p. p = 3. Цифры десятичного представления числа p достаточно случайны, что дает повод для математических курьезов и околонаучных спекуляций. Например, можно смело утверждать, что в разложении p встретятся шесть подряд девяток, и действительно, в пятом столбце третья снизу строка их содержит. Или страшнющие три шестерки, среди представленных цифр их нет (и очень хорошо), но они непременно появятся при увеличении количества рассматриваемых знаков. Чувствуете парадокс? В десятичном разложении p присутствует любая последовательность цифр, просто надо ее найти. В числе p сидят в закодированном виде все написанные и не написанные книги, любая информация, которая может быть выдумана, уже заложена в p. Надо только рассмотреть побольше знаков, найти нужный участок и расшифровать его. Это чем-то сродни парадоксу со стадом шимпанзе, долбящем по клавиатуре. При достаточно долгом (можно даже оценить это время) эксперименте они напечатают все пьесы Шекспира. Тут же напрашивается аналогия с периодически появляющимися сообщениями о том, что в Ветхом Завете, якобы, закодированы послания потомкам, поддающиеся прочтению с помощью хитроумных программ. Отметать сходу такую экзотическую особенность Библии не совсем мудро, кабаллисты веками занимаются поиском таких пророчеств, но хотелось бы привести сообщение одного исследователя, который с помощью компьютера нашел в Ветхом завете слова о том, что в Ветхом Завете нет никаких пророчеств. Скорее всего, в очень большом тексте, так же, как и в бесконечных цифрахp, можно не только закодировать любую информацию, но и “найти” фразы, изначально не заложенные туда. Очень хотелось бы ошибаться, так же, как хочется верить в сказки и чудеса. Ну а теперь я предлагаю на минуточку забыть, все, что вы прочитали о числе p и попробовать определить его, заходя совсем с другой стороны. Причем, обращаю внимание читателей, это будет вторая попытка журнала подобраться к числу p, первая была совершена в журнале "Hard'n'Soft" №8 2001 в статье Андрея Теплякова “Моделируя жизнь”, где успешно подтвердили первые знаки с помощью метода Монте-Карло. Важность таких попыток обусловлена, помимо любопытства, еще и гипотезой о том, что все (или некоторые) универсальные постоянные (постоянная Планка, число Эйлера, универсальная гравитационная постоянная, заряд электрона и т.д.) со временем меняют свои значения, так как меняется кривизна пространства из-за перераспределения материи или по другим, не известным нам причинам. Рискуя навлечь гнев просвещенного сообщества, можем предположить, что и рассматриваемое сегодня число p, отражающее свойства Вселенной, может со временем меняться. Во всяком случае, никто не может нам запретить заново найти значение p, подтвердив (или не подтвердив) имеющиеся значения. А начнем мы с далекой, казалось бы, области математики - теории простых чисел.
Математики нашли новое число - "Во", они прибавляют его к числу "Пи" и очень довольны Всякий, кто изучает простые
числа, бывает очарован и одновременно ощущает Возможно, из всех занимательных задач в теории чисел самая популярная - это поиск простых чисел. Подобно золотым самородкам, они скрываются в "породе" остальных чисел. Напомним, что простое число это то, которое не делится ни на какое другое кроме 1 и на само себя. Такие числа редки. Правда, у самых истоков реки Континуума (множества всех чисел), пока числа не велики, они встречаются довольно часто, но затем быстро растворяются в потоке, по мере того, как величина чисел растёт. Неравнодушно, если не сказать восторженно пишет о простых числах мэтр современной популярной математики Мартин Гарднер в своей книге "Математические досуги" (М.Мир 1972 стр. 410): "Ни одному другому разделу теории чисел не свойственно столько загадочности и изящества, как разделу, занимающемуся изучением простых чисел - непокорных упрямцев, упорно не желающих делиться ни на какие числа, кроме единицы и самих себя. Некоторые задачи, относящиеся к теории распределения простых чисел, формулируются настолько просто, что понять их может и ребёнок. Тем не менее они настолько глубоки и далеки от своего решения, что многие математики считают их вообще не разрешимыми. Может быть, в теории чисел так же как и в квантовой механике, действует своё собственное соотношение неопределённости и в некоторых её разделах имеет смысл говорить лишь о вероятности того или иного результата?" Некоторые статьи М. Гарднера из цитируемой книги выложены на лучшем головоломочном сайте Рунета http://www.golovolomka.hobby.ru , о простых числах статьи пока нет. Существуют различные способы поиска простых чисел. Можно даже построить специальное просеивающее устройство, подобное промывным желобам, которые старатели применяют при поиске самородков, но так или иначе их приходится искать, потому что никто не знает, где они встретятся. Есть, правда, кое-какие геологические приметы, по которым можно искать их залежи. Так же как когда-то тысячи золотоискателей бросились в Калифорнию и на Юкон промывать песок в горных речушках в поисках крупинок жёлтого металла, так и наши читатели могут отправиться в страну чисел, но налегке, вооружившись лишь этим маленьким руководством. (Аналогия золотых крупинок в песке заимствована из отличной статьи А.К. Дьюдни “Просеивание числового песка в поисках простых чисел” в “Scientific American” и выложенной на русском языке на http://www.helloworld.ru/texts/comp/algor/chisl/simple/index.htm ) Наверное, немногие математические понятия настолько доступны далёкому от математики человеку, как понятие простые числа. Любому встретившемуся на улице можно за минуту объяснить, что такое простые числа. Поняв, человек без труда напишет: 2,3.5,7,11,13,17 и т.д. Единица обычно не считается простым числом. Возможно ли распознать простые числа, как говориться, с первого взгляда? Если вы зачерпнули в сито сразу много чисел, сверкнёт ли среди них простое, как золотой самородок? Некоторые считают, что да. Например, числа оканчивающиеся на 1 часто оказываются искомыми, такие как 11,31,41. однако при этом следует быть осторожными и не принять фальшивое золото за чистое, как скажем, 21 или 81. По мере роста величины чисел, единица на конце всё чаще вводит в заблуждение. Создаётся даже впечатление будто простые числа в конце концов просто исчезают, как полагали некоторые древние греки. Ключевой вопрос математики: не все ли равно? (В. Шендерович) Существует ли последнее, самое большое по величине простое число? Первое дошедшее до нас доказательство того, что конца простым числам не существует, принадлежит Евклиду: предположим, что мы нашли самое большое простое число. Перемножим все известные простые числа и прибавим к произведению 1. Полученное число будет простым, так как при делении на любое число результат не будет целым, в остатке всегда будет 1. Не правда ли изящно? Хотя самого большого простого числа не существует вообще, но самое большое из тех, что нам известны, всё же есть. Это различие непонятно некоторым читателями даже журналистам. Вся беда заключается в этих заголовках на последней странице газет и журналов: НАЙДЕНО САМОЕ БОЛЬШОЕ ПРОСТОЕ ЧИСЛО! Иногда эта путаница продолжается и в самом сообщении, из которого мы узнаём, например, что с помощью нового суперкомпьютера только что удалось доказать, что число, содержащее 7067 знаков, а именно 5*223473+1 является простым. У него нет делителей, кроме 1 и, конечно, самого себя. В сообщении может отсутствовать напоминание (или читатель может проглядеть его) о том, что это самое большое из известных простых чисел, и что вскоре, возможно, будет найдено новое, ещё большее простое число. Поэтому приводим десятку самых больших из известных на сегодня простых чисел по данным http://www.utm.edu/research/primes/largest.html
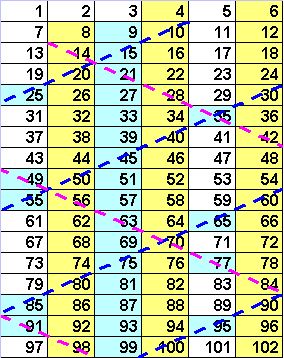
Там же узнаем, что 1 июня 1999 года Наян Найратвала, Георг Волтман, Скотт Куровски и другие открыли новое наибольшее простое число: 26972593-1. Это 38-е число Мерсенна и четвертое число Мерсенна, найденное в рамках проекта GIMPS (the Great Internet Mersenne Prime Search) запущенного Волтманом в начале 1996 года. Домашний Компьютер Найратвала (350 МгГц) проработал 111 дней, выполняя распределенные через Сеть вычисления во время простоя процессора. Распределенные вычисления (peer to peer или p2p) популярны в последнее время. Каждый желающий, например, может принять участие в поиске сигналов от внеземного разума, подключившись к проекту SETI@home (http://setiathome.ssl.berkeley.edu). Когда процессор простаивает, то вместо летающего пластилинового кольца или другого хранителя экрана ваш компьютер будет обрабатывать закаченную партию данных и отправлять результаты на центральный сервер проекта. Таким образом объединяются вычислительные ресурсы тысяч участников проекта и каждый из них может стать счастливым первооткрывателем Разумного сигнала из Космоса. Популярен такой же проект перебора молекулярных соединений для поиска лекарства от рака. Впрочем, пессимисты-журналисты считают это не более, чем рекламным трюком спонсоров проекта, а самые злые из них уверены, что под красивыми названиями злоумышленники используют гигантскую совокупную мощь для вскрытия паролей и шифров, созданных с помощью стойких криптопротоколов. Есть и специальный проект распределенных вычислений, официально нацеленный на вскрытие шифра, каждый желающий может поучаствовать, и, если именно его компьютер поставит завершающую точку, получит крупный приз ($2000!). Подключиться к проекту можно на www.myportal.ru/team . Но мы отвлеклись. Числами Мерсенна в честь французского математика-любителя Марена Мерсенна называются простые числа, имеющую фурму 2n-1. Мерсенн впервые заметил, что среди таких чисел много простых. В течение почти 200 лет математики подозревали, что число Мерсенна 267-1 простое, пока в 1903 году Нью-Йоркский профессор Коул не показал, что это число является произведением двух чисел 193 707 721 и 761 838 257 287. На вопрос, сколько он потратил времени, чтобы разложить число на множители, Коул ответил: “Все воскресенья в течение трёх лет”. Другой любитель С. Йетс из Делри-Бич (шт. Флорида, США) собрал в своей коллекции все известные простые числа, большие 1000. Его коллекция полна и точна. Так в чём же состоит основная трудность “одомашивания” простых чисел? В том, что они распределены среди всех целых чисел по закону, носящему заведомо невероятностный характер, но, тем не менее, не поддающемуся всем попыткам установить его. Представляете, какой вызов математикам, привыкшим, что все последовательности послушны им, то есть имеют формулу, по которой можно вычислить любое число по его номеру в последовательности? А тут вдруг элементарнейшие, примитивные до безобразия, всего лишь, не имеющие делителей, числа, и вдруг такая строптивость! Дерзкий вызов упрямых чисел принимали многие великие математики, но общей формулы так и нет! Чему равно сотое простое число? Единственный способ ответить на этот вопрос для математика состоит в том, чтобы составить список простых чисел и посмотреть, какое из них стоит на сотом месте. Как же составить такой список? Простейший метод состоит в том, чтобы перебирать одно за другим все целые числа подряд, вычёркивая составные (непростые). Разумеется, с помощью компьютера подобный перебор можно производить необычайно быстро, однако, по существу такое решение ничем не отличается от процедуры, предложенной около 2000 лет назад астрономом и географом из Александрии Эратосфеном. Процедура поиска простых чисел заключается в следующем: Пишется ряд чисел подряд, начиная с 1 (то есть течёт наша река Континуум), единица пропускается, следующее простое число - 2. Из ряда чисел вычёркиваются все числа, делящиеся на 2 (чётные). Следующее число 3 - вычёркиваются все числа, делящиеся на 3. Следующее число 5 ( а не 4 - мы его вычеркнули вместе со всеми чётными числами), потом 7, потом 11,13,17 и т.д. Постепенно составные числа будут зачёркнуты, а простые останутся. Для большей наглядности воспользуемся таблицей, имеющей в каждом ряду 6 цифр.
Сначала вычеркнем все четные числа, кроме двойки, это три столбика с желтым фоном. Потом вычеркнем числа кратные трем кроме самой тройки - это голубой столбик. Столбик под шестеркой уже вычеркнут как четный. Теперь избавляемся от чисел, кратных пяти, проводя синие пунктирные линии, впрочем, надо будет отметить только 25,35,55,65,85 и 95, так как остальные числа вычеркнуты ранее. Также делаем и с 7 - проводим розовую пунктирную линию, вычеркивая оставшиеся 49,77 и 91. Больше ничего вычеркивать не надо - числа кратные 8, 9 и 10 вычеркнуты при удалении соответственно четных и кратных трем. А более крупные делители проверять нет смысла - делители проверяются только до квадратного корня из общего количества проверяемых чисел. Оставшиеся числа и есть все простые числа, меньшие 100, или, точнее, 102, раз уж это число оказалось в таблице. Кстати, вопрос для продвинутых юзеров - как бы вы получили такую таблицу, не набирая все 100 (даже 102) чисел? А сколько цифр содержат первые 100 (ладно, 102) чисел? Не торопитесь с ответом. Раскроем секрет, для многих, наверняка, известный - в EXCEL в ячейке A1 вводим выражение =(СТРОКА()-1)*6+СТОЛБЕЦ() потом распространяем его на нужный диапазон, получая нужную таблицу за несколько секунд. Но, если будем отвлекаться, нам никогда не найти наше p. Строго упорядоченный алгоритм решета Эратосфена наводит на мысль, будто найти формулу, позволяющую хотя бы указать точное число простых чисел на любом интервале числовой оси, - дело не такое уж трудное. Но сколько ни бились математики, им так и не удалось найти желанную формулу. В начале позапрошлого века была высказана (подкреплённая наблюдением за простыми числами) гипотеза, согласно которой число простых чисел, меньших данного числа n, приближённо выражается соотношением n/ln(n) (ln - натуральный логарифм) и что данное приближение тем лучше, чем больше число n. Эта удивительная теорема, известная под названием “теорема об асимптотическом распределении простых чисел”, была строго доказана в 1896 году. Так насколько же быстро простые числа разрежаются по течению реки Континуума? Из первых 10 чисел 4 являются простыми, таким образом, их доля 40%. В первой сотне их содержание падает до 25% и оно продолжает падать с ростом величины чисел более или менее регулярно. Если взять отношение всех простых чисел, меньших n (по приведённой формуле) к числу всех рассматриваемых чисел n, то получим, что вниз по течению Континуума простые числа разрежаются пропорционально натуральному логарифму от n. Найти редкие оазисы простых чисел, затерянные в обширных пустынях составных чисел, покрывающих всё большие и большие интервалы числовой оси, нелегко. Существуют миллионы простых чисел, имеющих ровно 100 цифр, но пока ни одно такое число не обнаружено. Долгое время рекордно большим среди известных простых чисел являлось число 211231-1. Запись его содержит около 3376 цифр, а обнаружил его в 1963 году с помощью ЭВМ Дональд Б. Джиллис. До того как были изобретены современные компьютеры, проверка даже шести- или семизначных чисел требовала нескольких недель утомительных вычислений. Эйлер как-то заявил, будто число 1 000 009 - простое, но позднее обнаружил, что оно является произведением двух простые числа 293 и 3413. По тем временам это было крупным достижением, если к тому же учесть, что Эйлеру было за 70 лет и он к этому времени потерял зрение. Пьера Ферма в одном из писем спросили, простое ли число 100 895 589 169. В ответном письме Ферма сообщил, что это число разлагается на произведение простых сомножителей 898 423 и 112 303. Подобные результаты наводят на мысль, что старые мастера могли владеть каким то ныне утерянным секретом, позволявшим им с лёгкостью разлагать числа на множители. В 1874 году У. Стенли Джевонс вопрошал в своей книге “Основы науки”: “Может ли читатель сказать, произведение каких двух чисел равно 8 616 460 799? Думаю, что вряд ли, кроме меня самого, сумеет дать ответ на этот вопрос, ибо это два больших простых числа”. Джевонсу не следовало бы столь опрометчиво делать заключения о скорости действия будущей вычислительной техники. Компьютер позволяет найти оба числа (96 079 и 89 681) за несколько секунд. Генри Э. Дьюдени ещё в 1907 году отметил, что 11 - не единственное из известных простых чисел, которое состоит из одних лишь единиц. (Число, состоящее из повторения любой другой цифры, очевидно, составное). Дьюдени сумел доказать, что все числа, состоящие из 3,4,…,18, единиц составные. Дьюдени заинтересовал вопрос, существуют ли более чем 18-значные простые числа, запись которых состоит из одних лишь единиц. Ответ на этот вопрос нашёл один из читателей Дьюдени: он доказал, что 19-значное число 1 111 111 111 111 111 - простое. Позднее было доказано, что число, записанное с помощью 23 единиц, тоже простое. Ответы на многие вопросы, связанные с “единичными” числами, неизвестны до сих пор. Никто не знает, существует ли среди них бесконечно много простых чисел и даже существует ли вообще четвёртое простое число, записанное с помощью одних единиц. Ближайший кандидат в простые числа состоит из 47 единиц (числа из 29,31,37,41,43,53,61 и 73 единиц составные). Ученые нашли последнее число в разложении числа "Пи" - им оказлось число "е" В зависимости от расположения целых чисел простые числа могут образовывать тот или иной узор. Однажды математику Станиславу М. Уламу пришлось присутствовать на одном очень длинном и очень скучном, по его словам, докладе. Чтобы как-то развлечься, он начал писать на клетчатой бумаге числа, поставив в центре 1 и двигаясь по спирали против часовой стрелки. Без всякой задней мысли он обводил все простые числа кружками. Вскоре, к его удивлению, кружки с поразительным упорством стали выстраиваться вдоль прямых. На приведённом рисунке, полученном на компьютере, продублировано то, что Улам сделал от руки. Простые числа выделены чёрными точками, а составные - белые квадраты.
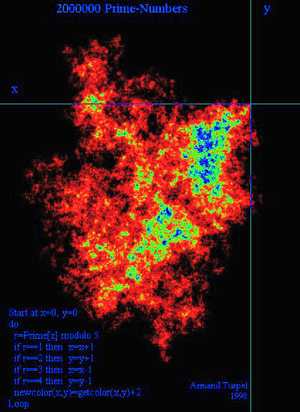
Выделяющиеся тёмные линии - это залежи простых чисел. Вблизи центра выстраивания простых чисел вдоль прямых ещё можно было ожидать, поскольку плотность простых чисел вначале велика и все они, кроме числа 2, нечётны. Если клетки шахматной доски перенумеровать по спирали, то все нечётные числа попадут на клетки одного и того же цвета. Взяв 17 пешек (соответствующих 17 простым числам, не превосходящим числа 64) и расставив их наугад на клетки одного цвета, вы обнаружите, что пешки выстроились вдоль диагональных прямых. Однако не было оснований ожидать, что и в области больших чисел, где плотность простых чисел значительно меньше, те так же будут выстраиваться вдоль прямых. Улама заинтересовало, как же будет выглядеть его спираль, если её продолжить до нескольких тысяч простых чисел. Разработав программу, Улам получил рисунок для чисел от 1 до 65 000 (иногда его называют “скатертью Улама”), из которого видно, что даже у края картины простые числа продолжают послушно укладываться на прямые. Участкам прямых соответствуют квадратные трехчлены, порождающие простые числа, например X2+X+17, или найденный Эйлером X2+X+41, у которого первые 40 решений - простые (при подстановке X=0,1,2…40), а из 2398 первых значений ровно половина - простые! В книге, процитированной в эпиграфе этой главы, приводиться рисунок, на котором числа подряд выписаны в форме прямоугольного треугольника и простые числа отмечены кружками. И, что самое интересное, эти кружки тоже расположены по прямым линиям. А сможете ли вы написать программу, просто (для начала) заполняющую плоскость по раскручивающейся квадратной спирали? Задача интересная не только для начинающих программистов. Предлагаем также читателям представить простые числа в какой-нибудь другой наглядной форме. Но, главное, предлагаем так же поискать новое простое число, их ведь очень много не найдено, даже не очень больших. Когда прославитесь, не забудьте сослаться на “Hard’n’Soft”. Исследователи, занимающиеся изучением простых чисел любят их и получают удовольствие от общения с ними. Так, на http://www.2357.a-tu.net вы найдете не только симпатичный апплетик, выводящий постоянно на экран простые числа, но и сможете послушать музыку (midi-файлы), сгенерированную ими (не хуже многих популярных мелодий), и посмотреть созданные простыми числами картины. Например, такую.
Алгоритм создания этой картины незатейлив: берется простое число, определяется остаток от деления его на 5, в зависимости от его (остатка) значения происходит сдвиг от текущей точки в одном из четырех (+X,-X,+Y,-Y) направлений и новая точка подсвечивается с учетом ее предыдущей яркости. Цикл повторяется (в данном примере) 2000000 раз. Естественно, что 2 миллиона простых чисел вычислены заранее и сидят во вспомогательном файле. И самое непостижимое нашим умом явление - точки не рассыпаются в бесконечность, а собираются в некий звездно-плазменный факел с протуберанцами, как бы пытаясь сообщить нам свои скрытые закономерности. Чтобы не закрепилось впечатление пустопорожних разговоров, приводим распечатку программы, печатающей на экране все простые числа до 1000. Программа написана в среде FoxPro, её язык прост и понятен, похож на Бейсик. CLEAR && 1 очистка
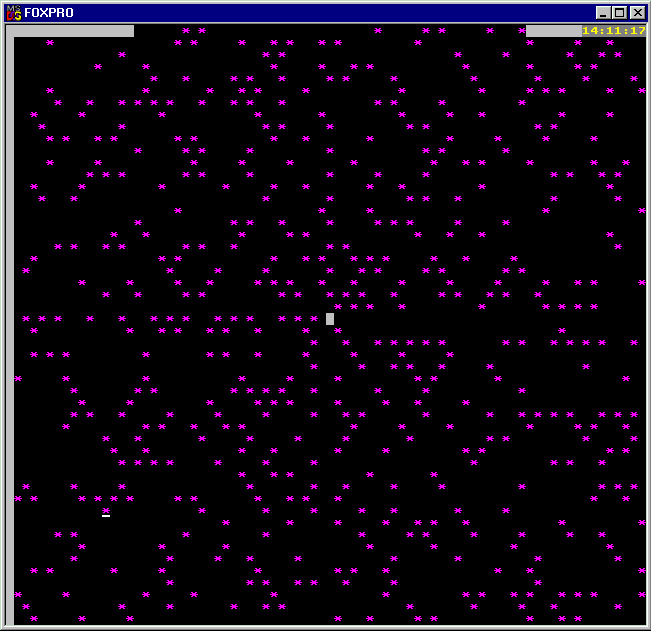
экрана В 21-й строке функция STR(K) превращает числовую переменную в строковую для вывода на экран, функция alltrim() убирает лишние пробелы. Сердцевина программы - функция MOD(K,I), которая выдаёт остаток от деления первого числа на второе. Если остаток равен нулю, значит первое число делится на второе, дальше это число проверять нет смысла, так как ясно, что оно не простое. Обратите внимание на строку №8 - как мы уже отмечали выше, поиск делителей надо производить только до числа, равному квадратному корню из общего числа проверяемых чисел, так как большие делители дадут меньшее частное от деления, которое уже проверялось. (Эта задача, кстати, присутствует в тестах для поступающих в ВУЗ.) Для улучшения программы можно предложить проверять делимость не на все числа, а только на уже найденные простые, которые придётся хранить в специальном массиве, и обновлять его при каждом новом найденном простом числе. Приведу еще и “личную” скатерть Улама, полученную также на FoxPro для DOS’a в текстовом режиме 80х48
Относительно маятника Вселенная все время мотается туда-сюда. (В. Шендерович) Теперь, наконец, мы вооружены знаниями и инструментарием и можем приступить к запланированной цели - проверке нашего p. Для этого мы воспользуемся известным предположением теории чисел: вероятность, что два числа взаимно просты равна 6/p2 Взаимно простыми называются числа, не имеющие общих делителей (для строгости обычно добавляют “кроме единицы”). Какой же алгоритм наших действий? Берем два случайных числа, находим их делители и сравниваем их. Повторяя процесс в цикле, вычисляем долю шагов цикла (от общего числа шагов), при которых числа не имели общих делителей. Разделив 6 на эту долю и извлеча (есть такое слово?) квадратный корень из частного, получим искомое значение p. Для достоверности эксперимента проведем серию таких циклов, находя среднее значение результата. Текст программы на VB6.0. Результат выводится в файл. (Отступы в html пропали, но это не страшно :-) Dim a(100) As Integer Dim b(100) As
Integer А вот и результат нашего поиска. Напомню, что u - доля взаимно простых чисел от числа шагов в серии (uu), priznak - количество случаев с общими делителями в серии из u опытов, pi - искомое число по результатам обработки последнего цикла и pi1 - среднее значение результата по итогам 20 серий циклов. uu= 0,5844156 priznak= 416 u= 1001 pi= 3,204164 pi1=
3,204164 О чем говорит наш результат? Изменилось p? Если да, то как это отразится на окружающем мире - изменится ли количество воды в чайнике, траектория планет и спутников, оптимальная форма и раскраска арбузов, плотность мозговых извилин? Если серьезно, то результат довольно неплохой с учетом того, что значение 6/ p2 является оценочным, ведь распределение простых и взаимно простых чисел не поддается никаким точным законам. Результат работы программы будет зависеть от количества серий, от глубины цикла, от диапазона (у нас было 1000), в котором выбираются числа, и возможно от “случайности” датчика случайных чисел. Повторите на вашем компьютере, может, получите более точное значение p. С надеждой на это и закончим. Представленные рассуждения не претендуют на академическую щепетильность и предполагают наличие чувства юмора, особенно при разговоре о непостоянстве постоянной Планка. |
| Автор | )c( 2000-2019 Kопирайта нет, копируйте на здоровье :) 100112 лет в Интернете |
|