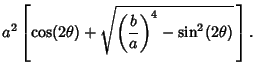Космические овалы Кассини

Да вьется всегда вокруг цепи правил серебряная нить фантазии!
Роберт Шуман

Древние греки превозносили сферу, считая ее законченной самодостаточной идеальной формой, лежащей в основании мироздания. Многие помнят, наверное, старинную гравюру, на которой траектории небесных светил моделировались вписанными в сферу Платоновыми телами – этакая всеобщая гармония мира. Законы Кеплера, первый из которых говорит, что планеты движутся по эллипсам, в одном из фокусов которых находится Солнце, разрушил многовековую птолемееву идиллию, развенчал культ сферы. Сам Кеплер был в шоке от такого «варварства», если верить (12). Хотя до сих пор мы говорим по привычке «в высших сферах» или «сфера деятельности», отдавая дань античной красивости мира.

Напомним определение эллипса – это плоская фигура, у которой для каждой точки сумма расстояний от двух фиксированных точек (полюсов) постоянна. От соотношения расстояний между фокусами и этой суммы расстояний (или от соотношения полуосей) можно получить разные фигуры – от круга до (постепенно сплющиваясь) вырождения в линию. Если котенок сидит на лестнице, низ которой скользит по полу, а верх не отрывается от стены, то котенок опишет траекторию эллипса. Причем, если он сидит посередине лестницы, то опишет дугу окружности. Если на верхнем или на нижнем конце лестницы, то траектория выродится в прямую линию. Поэкспериментируйте на досуге.

Занимательные задачи, связанные с эллипсом основаны на его отражательных свойствах – лучи, выйдя из одного фокуса, обязательно соберутся в другом. А если не из фокуса? У Мартина Гарднера рассматривается бильярдный стол в форме эллипса. Так вот, если послать шар так, чтобы он не пересек отрезок между фокусами, то он так и будет кататься, не пересекая этот отрезок, заметая поверхность вокруг воображаемого эллипса меньших размеров. Если же послать шар (из произвольной точки) так, чтобы он пересек отрезок между фокусами эллипса, то он так и будет двигаться, каждый раз пересекая этот отрезок и касаясь двух воображаемых ветвей гипербол с фокусами в фокусах эллипса.  Желающие могут реализовать эту забаву в виде аплета – прекрасное пособие для изучения эллипса.

И этюд для технологов – как расточить эллиптическое отверстие? Можно, конечно, почитать второй том классической «Технологии машиностроения» Соколовского, не переиздававшейся с 1948 года, но лучше попробовать свои силенки.

А еще можно в уравнении эллипса x² / a² + y ² / b ² = r ² попробовать поменять показатель степени, брать не 2, а от 0 до, предположим, 10, прорисовать совместно и проследить, как меняется форма от ромба до прямоугольника.

Пока на время распрощаемся с эллипсом. Теперь представьте любителя математики рассматривающего определение эллипса… Вполне естественно, что у него мелькнет мысль – а что, если постоянным будет не сумма расстояний от двух точек, а их произведение? Не поленитесь, попробуйте – напишите формулы расстояний от текущей точки с координатами x, y до фокусов (-а,0) и (а,0), перемножьте их и попробуйте привести полученное уравнение четвертой степени к «красивому» виду. Это уравнение и соответствует так называемым овалам Кассини. Знаете почему?

Джовани Кассини родился в 1625 году в Италии и прожил 87 лет. Обучался в школе иезуитов в Генуе. В 1648-1649 годах работал наблюдателем в обсерватории Панзано. За свои познания в астрономии (а еще он добился успехов в гидравлике, оптике, картографии) он был приглашен в 1650 году сенатором Болоньи маркизом Корнелом Малвасиа на должность профессора астрономии для расчета астрологических таблиц. В 1663-1665 годах по личному указанию Папы Римского Кассини руководил работами по защите от наводнений и реконструкции мостов, это нам не так интересно. Он наблюдал комету 1652-53 годов и посвятил ее герцогу Модены, описал для королевы Швеции Кристины (бывшей тогда в изгнании в Италии) появление кометы 1656 года. В 1664 году Кассини сделал вывод о том, что кометы вращаются вокруг Солнца по вытянутым в направлении Сириуса орбитам.

В том же 1664 году Кассини получил в распоряжение мощный телескоп, линзы для которого изготовил лучший тогда мастер Гиусепп, что позволило сделать целый ряд замечательных открытий. В июле 1664 он измерил период вращения Юпитера вокруг своей оси, обнаружил полосы и пятна на этой планете, увидел, что планета была сплющена между полюсами. В 1666 он измерил период вращения Марса вокруг своей  оси, получив точность в пределах трех минут, и наблюдал поверхность этой планеты. Он первым описал детальные наблюдения лун Юпитера в 1668 году. Тогда еще были обнаружены некоторые несоответствия данных, которые астрономы смогли объяснить позже, только зная значение скорости света. Правильнее сказать, именно эти расхождения в появлении спутников Юпитера в зависимости от положения Земли, когда путь света удлинялся за счет орбиты Земли, и были наглядной иллюстрацией конечности скорости света. Скорость света вычислил О.К.Ремер в 1676 году, пользуясь именно данными Кассини о движении спутников Юпитера.

Репутация ученого была необычайно высока. В 1667 году Джовани Кассини был приглашен в Париж для организации обсерватории и остался во Франции до конца жизни. В Париже Кассини продолжал делать революционные открытия – открыл четыре спутника Сатурна, в 1675 году открыл промежуток между кольцами Сатурна, шириной 5000км. Он так и называется сейчас – «щель Кассини». Также он впервые предложил, что кольца Сатурна состоят из камней разных размеров.

В 1659 году Кассини познакомился с данными наблюдений Тихо Браге, которые тот пытался увязать с геоцентрической системой, а позже принял теорию Коперника о гелиоцентризме. Известны также многочисленные работы Джовани Кассини уже вместе с сыном Якусом Кассини по синхронизации часов на Земле, по изучению сплюснутости нашей планеты, по измерению парижского меридиана. В 1709 году Кассини передал руководство астрономией сыну, так как стал терять зрение. Современники вспоминали, что глубокая религиозность помогала ослепшему ученому не терять бодрость духа и обычную доброту.

Не случайно благодарные потомки назвали автоматическую космическую станцию, летящую к Юпитеру и Сатурну именем великого астронома Кассини. (17)

Но самое главное для нас в этом историческом путешествии то, что в 1680 Джовани Кассини изучал кривую Кассиниану, которая является геометрическим местом точек, чье произведение расстояний от двух фиксированных фокусов постоянно. Он работал над этой кривой в процессе изучения относительных движений Земли и Солнца и предложил это как кривая для планетарных орбит подходит больше, чем эллипс, предложенный Кеплером. Открытая чуть позже лемниската Якоба Бернулли была частным случаем овала Кассини, но это не было осознано математиками в течение ста лет.

По каким же орбитам движутся планеты? При маленьком эксцентриситете (у орбиты Марса полуоси отличаются на 1/11 часть, у орбиты Земли – на 1/65) линии эллипса и овала Кассини практически совпадают… И, все-таки, при всем восхищении перед великим астрономом, мы должны признать, что согласно законам Ньютона и закону всемирного тяготения, траектории движения тел описывается эллипсом или параболой в зависимости от начальных условий. Хотя споры о виде траектории идут до сих пор и шансы овалов Кассини на приоритет по прежнему велики. (15) Но эти споры никак не отразятся на нашем желании поиграть с замечательным овалом, или точнее, овалами, так как их два… или один, точнее, то два, то один.

Итак, мы записали произведение расстояний от двух фокусов:

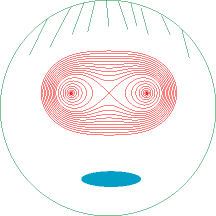
Теперь мы можем проделать опыт, который мы делали в статье про улитку Паскаля – перенесем свободный член влево от знака равенства, но приравняем полученный многочлен не нулю, а некоторой переменной k, из которой мы получим значения красной, синей и зеленой составляющей цвета. Запуcтив процесс в цикле по координатам x и y, мы сразу получим потрясающий рисунок.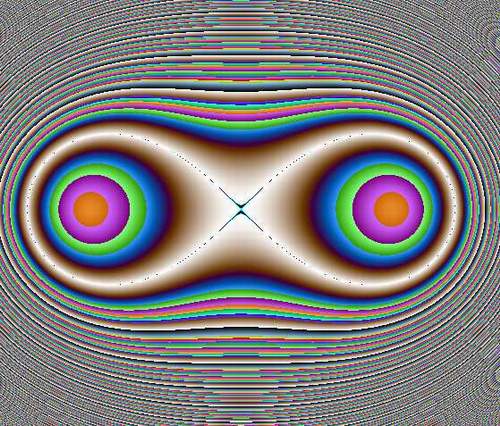

Ну, не совсем сразу, а чуть повозившись с масштабами и коэффициентами при выборе цвета, но дело стоит того.

Private Sub Комманда1_Click() pi = 4 * Atn(1) xmax = 600 ymax = 500 scal = 15 For x = ss To xmax Step ss For y = ss To ymax Step ss xx = (x - 270) / scal yy = -(y - ymax / 2) / scal K = (1 * xx ^ 2 + 1 * yy ^ 2) ^ 2 - 254 * (1 * xx ^ 2 - 1 * yy ^ 2) - 14 K = Abs(K) red = Abs(255 - (0.03 * K)) Mod 255 green = Abs(255 - (0.04 * K)) Mod 255 blue = Abs(255 - (0.05 * K)) Mod 255 Col = RGB(red, green, blue) If ss > 1 Then Line (x + 90, y)-Step(ss, ss), Col, BF If ss = 1 Then PSet (x + 90, y), Col Next y Next x End Sub

Рассмотрим получившуюся картинку. Мы видим на ней как обычные овалы при движении от периферии к центру начинают сужаться, появляется утоньшение посередине и потом перемычка, потом рисунок распадается на две части. Все эти кривые и есть семейство овалов Кассини. А вид их зависит от соотношения параметров a и b.

При значениях b > a * sqr(2) фигура выпуклая как эллипс.

При b =а* sqr (2)появляются прямые участки, фигура имеет вид как на рисунке слева.

При а < b < a * sqr(2) появляется вогнутая перемычка с четырьмя точками перегиба.

При a = b перемычка смыкается, полученная фигура называется лемнискатой Бернулли.

При a > b фигура разваливается на два овала.

То есть, на нашем первом рисунке мы сразу получили все семейство овалов Кассини.

С чего же мы начнем наши попытки нарисовать овалы Кассини по настоящему, чтобы поиграть с ними? Для рисования функции необходимо или явно выразить одну переменную через другую – но для этого пришлось бы решать уравнение четвертой степени, либо задать обе координаты в параметрическом виде – мне не встретилось нигде такое представление овалов Кассини. Или же, третий вариант, нарисовать все в полярных координатах, тем более что формула относительно не сложная:

r ² = 

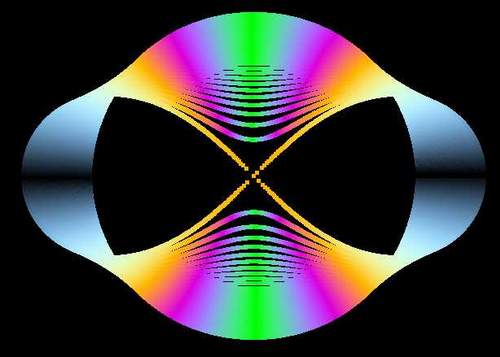
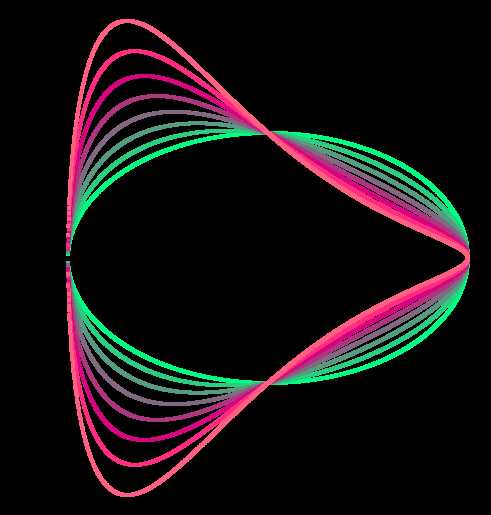
Причем, сразу начнем с экспериментов – нарисуем не один овал, а в цикле будем менять параметр a (напомню - половина межфокусного расстояния). И результат:

Обратите внимание, как «расползался» овал от окружности (а=0) до Лемнискаты Бернулли (a = b ). И код этого чуда с глазами и ушами:

Private Sub Комманда1_Click() Cls DrawWidth = 2 pi = 4 * Atn(1) x0 = 350 y0 = 180 aa = 200 b = 200 ss = 3 xx1 = 0: yy1 = 0 For a = 20 To aa Step 5 For f = 0 To pi * 2 Step 0.001 If KeyAscii = 32 Then End t = (b / a) ^ 4 - (Sin(2 * f)) ^ 2 If t > 0 Then t1 = Cos(2 * f) + (t) ^ 0.5 If t1 > 0 Then r = a * (t1) ^ 0.5 qrr = Abs(255 * Sin(f * 2)) qgg = Abs(255 * Sin(f * 3)) qbb = Abs(255 * Sin(f * 4)) col = RGB(qrr, qgg, qbb) xx = r * Cos(f) yy = r * Sin(f) If ss > 1 Then Line (xx + 350, yy + 300)-Step(ss, ss), col, BF If ss = 1 Then PSet (xx + 350, yy + 300), col Else zzzz = 0 End If Next f Next a End Sub

Оба подкоренных выражения вынесены в отдельные вспомогательные переменные с проверкой на положительность, впрочем, это технические мелочи.

Обратите внимание на раскраску – красная, синяя и зеленая составляющие привязаны к параметру f – центральному углу, что и дает радужные радиальные полосы. Можно было привязаться и к текущему радиусу или к комбинации угла и радиуса, попробуйте сами. А мы пока зададимся естественно вытекающим из предыдущего опыта вопросом – а что, если менять в цикле не фокусные расстояния, а радиус (точнее значение произведения двух радиусов), или, в наших обозначениях, переменную b. Сказано – сделано:

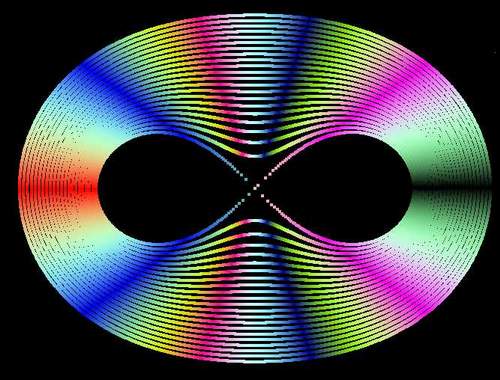
Мы снова получили, как и на первом рисунке семейство овалов Кассини с фиксированными фокусами. Доработка кода была минимальной – вместо цикла по переменной а (межфокусное расстояние) запустили цикл по переменной b (произведение радиусов). Вот и код:

Private Sub Комманда1_Click() Cls DrawWidth = 2 pi = 4 * Atn(1) x0 = 350 y0 = 180 a = 150 bb = 280 ss = 2 xx1 = 0: yy1 = 0 For b = 150 To bb Step 6 For f = 0 To 2 * pi Step 0.0041 If KeyAscii = 32 Then End t = (b / a) ^ 4 - (Sin(2 * f)) ^ 2 If t > 0 Then t1 = Cos(2 * f) + (t) ^ 0.5 If t1 > 0 Then r = a * (t1) ^ 0.5 qrr = Abs(255 * Sin(f * 2.5)) qgg = Abs(255 * Sin(f * 5)) qbb = Abs(255 * Sin(f * 3)) col = RGB(qrr, qgg, qbb) xx = r * Cos(f) yy = r * Sin(f) If ss > 1 Then Line (xx + 350, yy + 300)-Step(ss, ss), col, BF If ss = 1 Then PSet (xx + 350, yy + 300), col Else zzzz = 0 End If Next f Next b End Sub

Все ли хорошо? Нет… смущает пустота в распавшихся на две части зонах…  Цикл специально прерывался (точнее, начинался) при значении a = b, ибо при попытке прорисовать распадающиеся части выявляются неопознанные артефакты:

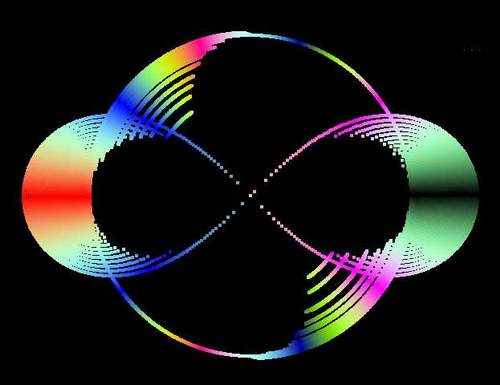
Рисунок, конечно, сам по себе красивый, но мы-то движемся к намеченной цели, а тут – неизвестно что. (Код такой же, как и в предыдущем случае, только внешний цикл имеет вид «For b = a To 0 Step -6»). Во-первых – не прорисованы внутренние зоны обоих овалов, а во-вторых – непонятные вылезания «наружу». Как избавиться от глюков? Первая мысль – неправильно отрабатывает синус, ибо, кто же винит в первую очередь себя? Потом станет стыдно за такие мысли… Но что делать? Морщим лоб, чешем репу в наивной попытке озарения…

Ну, конечно же – надо брать оба знака после вычисления квадратного корня, а у нас был предусмотрено только положительное значение… засучиваем рукава и… так и есть – начали прорисовываться внутренние области. В программе это реализовано вводом вспомогательных переменных k и j, которые постоянно меняют свой знак, а так, как мы проверяем знак подкоренного выражения, то к ошибке это не приводит, зато выводит внутренние области овалов. Для избавления от «вылезаний наружу» тоже находится средство – при построении развалившихся областей надо давать ограничения по полярному углу.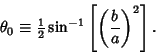

Но в Visual Basic’e (и в других популярных языках программирования) нет арксинуса, есть только арктангенс. Поэтому формулу чуть-чуть дорабатываем и имеем желанный результат:

Вот они, эти глаза из космоса, в виде кода:

Private Sub Комманда1_Click() Cls DrawWidth = 2 pi = 4 * Atn(1) x0 = 350 y0 = 180 a = 200 bb = 280 ss = 2 ReDim x1(num), y1(num), a1(num), L1(num) xx1 = 0: yy1 = 0: k = 1: j = 1 For b = a To 20 Step -4 For f = 0 To 2 * pi Step 0.001241 If KeyAscii = 32 Then End k = -k If k = -1 And j = 1 Then j = -j u = 10 If b < a Then u = 0.42 * Atn((b / (a ^ 2 - b ^ 2) ^ 0.5) ^ 2) If (f < u Or f > (2 * pi - u)) Or (f > pi - u And f < pi + u) Then t = ((b / a) ^ 4 - (Sin(2 * f)) ^ 2) If t > 0 Then t1 = (Cos(2 * f) + k * (t) ^ 0.5) If t1 > 0 Then r = a * (t1) ^ 0.5 qrr = Abs(255 * Sin(f * 5 + pi / 2)) qgg = Abs(255 * Sin(f * 5.5)) qbb = Abs(255 * Sin(f * 3)) col = RGB(qrr, qgg, qbb) xx = r * Cos(f) yy = r * Sin(f) If ss > 1 Then Line (xx + 350, yy + 300)-Step(ss, ss), col, BF If ss = 1 Then PSet (xx + 350, yy + 300), col Else zzzz = 0 End If End If Next f Next b End Sub

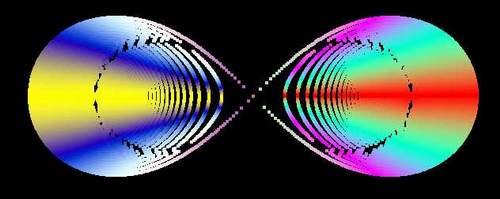
Естественно, что при определении границ существования углов надо не забыть и о втором овале, обычно о нем вспоминают после первого «одноглазого» рисунка. Для достоверности пришлось ввести коэффициент 0,42 – так как формула была приведена для овала единичного радиуса без учетов нашего масштаба.

Что еще интересного, спросите далее? Есть красивые продолжения. Дело в том, что рассмотренные овалы с двумя фокусами всего лишь частный случай овалов Кассини, обобщенных на произвольное количество фокусов. Это обобщение открыл и исследовал в 1843 году Серрет (Serret)  и он же назвал все множество именем великого астронома. А вот и формула:

Быстренько для проверки подставляем n =2 и убеждаемся, что это знакомые нам овалы (конечно, не удержались поменять а в цикле):

И видим старого знакомца с теми же, знакомыми глюками, значит, формула верная. И код программы:

Private Sub Комманда1_Click() Cls DrawWidth = 2 pi = 4 * Atn(1) x0 = 350 y0 = 180 ss = 2 n = 2 ReDim x1(num), y1(num), a1(num), L1(num) xx1 = 0: yy1 = 0: k = 1: j = 1 For a = 0 To 5 Step 0.25 For f = 0 To 8 * pi Step 0.001 If KeyAscii = 32 Then End If k = -1 And j = 1 Then j = -j t = (a - (Sin(n * f)) ^ 2) If t > 0 Then t1 = (Cos(n * f) + j * (t) ^ 0.5) If t1 > 0 Then r = bb * k * (t1) ^ (1 / n) qrr = Abs(255 * Sin(f * 5 + pi / 2)) qgg = Abs(255 * Sin(f * 5.5)) qbb = Abs(255 * Sin(f * 3)) col = RGB(qrr, qgg, qbb) xx = r * Cos(f) yy = r * Sin(f) If ss > 1 Then Line (xx + 350, yy + 300)-Step(ss, ss), col, BF If ss = 1 Then PSet (xx + 350, yy + 300), col Else zzzz = 0 End If 'End If k = -k: j = -j Next f Next a End Sub

Хотелось бы извиниться за использование одной и той же буквы, но думаю ясно, что в последних формулах «а» – это не межфокусное расстояние, как раньше, а масштабный коэффициент, учитывающий, что формулы даны для единичного радиуса. Тут же даем количество фокусов n равное трем:

И не в силах остановиться… это то же вихрь, который захватывает при рисовании циклоид и фигур Лиссажу, например, даем n=1.5

Все, усилием воли останавливаем эти чудесные опыты.

Еще три красивых, этюдных, момента.

Лемнискату Бернулли можно определить как геометрическое место точек, для которых произведение расстояний от двух фокусов равно квадрату половины расстояния между фокусами. Великий физик описал эту «похожую на 8 поверхность» в своей статье Acta Eruditorumon, вышедшей в 1694 году. К сожалению, он не знал, что его лемниската – частный случай овалов, описанных Кассини четырнадцатью годами ранее.

Лемнискату Бернулли можно также рассматривать как частный случай циссоиды. Определения циссоиды давать не будем, лучше сразу рассмотрим на примере.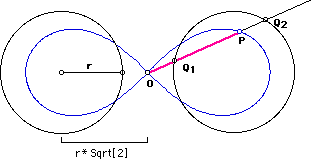

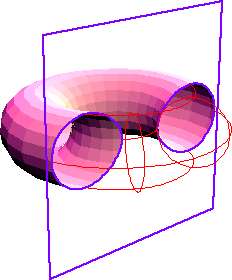
Выберем точку О, отстоящую от центра окружности с единичным радиусом на расстояние sqrt(2) и проведем из нее линию, пересекающую окружность в точках Q1 и Q2. Теперь сдвинем отрезок Q1Q2 вдоль линии до совмещения точки Q1 с точкой О. При движении отрезка точка Q2 будет рисовать циссоиду, в данном случае лемнискату Бернулли. Предлагаю желающим сделать аплетик и поиграть с другими значениями фокусного расстояния.

Спросите, чему равна площадь одного крыла бабочки лемнискаты Бернули? Если а – половина фокусного расстояния, то S = a²(!!!) без всяких там Пи и прочих коэффициентов, словно это обычная квадратная табуретка!

А знаете ли вы, какая фигура получится при разрезании тора (бублика)? Правильно – овалы Кассини. Разглядите картинки разрезанных торов и увидите там все варианты рассмотренных выше таких уже знакомых овалов Кассини.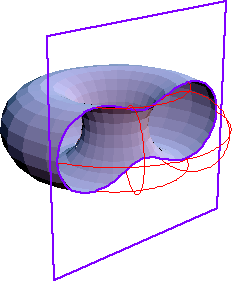

Когда снова придется кушать баранки – не забудьте разглядеть срез. Занимательные статьи о торе можете найти на Арбузе.

И последней не совсем серьезной темой, имеющей отдаленное отношение к овалам Кассини, будет теория яиц. Или, точнее, яйцевидных поверхностей. Собственно, поверхностью они станут после вращения вокруг продольной оси, а пока займемся поисками самого подходящего сечения. Самый простой способ – в определении эллипса ввести поправочку и рассматривать постоянство суммы расстояний от двух фокусов, но с учетом того, что расстояние от одного из фокусов умножается на постоянный коэффициент. Не поленитесь, попробуйте вывести уравнение яйцевидного эллипса и прорисовать при разных значениях искажающего коэффициента. Вряд ли вы найдете более интересное и востребованное времяпрепровождение. Куры должны быть благодарны аналитической геометрии. (Уравнение получится, предупреждаю, громоздким. По этой же причине не получилось исказить таким же образом овалы Кассини, хотя очень хотелось попробовать)

Разработаны различные методики яйцевидного искажения эллипсов. Одна из них задается уравнением (в символах Бейсика) X ^²+(1.4^x*1.6*y)² =1 для круга единичного радиуса, или равно R² в общем случае, откуда Y = sqr(R² - X² )/( R *1.6*1.4^x ). В общем-то, коэффициент 1.4 сразу вызвал подозрение, и решено было менять его в цикле, как показали опыты, от 1 до 1.007 с шагом 0.001, что вы и видите на картинке.

А вот и код этого набора яиц. Переменная n вспомогательная для раскраски.

Private Sub Комманда1_Click() Cls DrawWidth = 2 pi = 4 * Atn(1) x0 = 350 y0 = 180 a = 200 n=0 ss = 2 xx1 = 0: yy1 = 0: k = 1: j = 1 For b = 1# To 1.007 Step 0.001 For x = -a To a Step 0.1 If KeyAscii = 32 Then End If k = -1 And j = 1 Then j = -j t = (a ^ 2 - x ^ 2) If t > 0 Then y = k * t ^ 0.5 / (1.6 * b ^ x) qrr = Abs(43 * n) qgg = Abs(255 - 50 * n) qbb = Abs(128) col = RGB(qrr, qgg, qbb) xx = x yy = y If ss > 1 Then Line (xx + 350, yy + 300)-Step(ss, ss), col, BF If ss = 1 Then PSet (xx + 350, yy + 300), col Else zzzz = 0 End If k = -k: j = -j Next x n = n + 1 Next b End Sub

Продолжая эти столь важные для науки опыты, мы опытным путем находим идеальное значение возводимого в степень х коэффициента: 1.0014. Запомните это число и посмотрите на совершенную форму яйца, порождаемого им. Осталось только начать вращать его вокруг продольной оси, получить каркас, натянуть на него поверхность, дать тени и блики… и можно незаметно подложить наседке.

Но это все вы уже проделаете самостоятельно. Или вместе, но в следующий раз. Остался непременный атрибут всякого непотопляемого реферата – использованная литература, чем мы с удовольствием и займемся:

1. http://www.ipfw.edu/math/Coffman/pov/spiric.html - рассказано о сечениях тора с картинками на английском языке. Там же ссылки на биографии математиков и на замечательные кривые.

2. http://www.didaktik.mathematik.uni-wuerzburg.de/mathei/cinderella/cassoval.html  - ссылка на апплет, рисующий овалы Кассини, на немецком языке.

3. http://164.8.13.169/Enciklopedija/math/math/c/c084.htm страничка овалов Кассини сайта, посвященному замечательным кривым. Именно здесь была найдена подсказка насчет отрицательного значения корня и об ограничении рассматриваемых углов. На том же сайте и о лемнискате Бернулли - http://164.8.13.169/Enciklopedija/math/math/l/l200.htm

4. http://www-history.mcs.st-andrews.ac.uk/history/PictDisplay/Cassini.html - здесь найдены портреты великого астронома.