Бублики, планеты и колечки дыма.

Опубликовано в сокращении в  Компьютерре  №10/2000 

Бильбо уселся на скамеечку возле двери, скрестив ноги и выпустил красивое серое колечко дыма; оно поднялось вверх и поплыло вдаль над Холмом.
Дж.Р.Р.Толкин. «Хоббит, или туда и обратно».

…Бублики пекут из менее крутого теста, чем баранки. Бублики крупнее баранок, их кольца толще… На 1 кг приходится до 20 бубликов, от 25 до 50 баранок и до 250 сушек.
Книга о вкусной и здоровой пище. Пищепромиздат 1954г.

Из названия и эпиграфов следует, что сегодня речь пойдёт о торе. Вряд ли есть ещё какое-нибудь тело, с которым было бы связано столько интересных вопросов.

На колечки дыма, как случай тора, отвлекаться не будем, курильщики знают, как трудно выдуть кольцо и как интересно за ним наблюдать. Эти кольца довольно устойчивы, живут несколько минут и всё время вращаются. Лет 25 тому назад в «Кванте» была описана простейшая установка для получения колечек дыма и изучения их свойств.

Для начала классическое определение: тор – это поверхность, образованная вращением окружности вокруг оси, лежащей в плоскости окружности и не пересекающей её. Хотя, собственно, почему не пересекающей? Если да, получим тело, похожее на яблоко – тор с самопересечением. Как посчитать объём такого тора, если у «нормального» V=2ПиR²r²? Всё-всё, считать больше ничего не будем, это скучно и неинтересно. Другое дело – отправиться в космос на межпланетную станцию. Если верить фантастам (а кому же ещё верить?), то эти самые станции будут в виде тора для создания искусственного тяготения за счёт вращения. На рис.1 можно увидеть такую станцию, картинка входит в пакет MS PLUS98. 

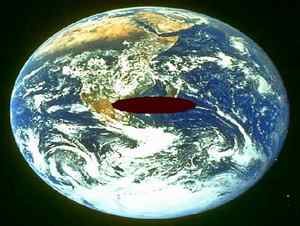
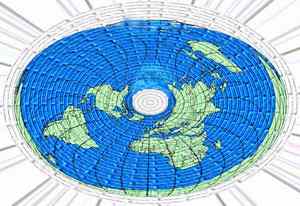
Итак, мы внутри. Где верх, где низ? Что покажет отвес и как будет падать груз – по отвесу, или нет? А вдруг (о, ужас!) центр масс станции не совпадёт с осью вращения, как будем вращаться? Теперь выглянем в окно (не дома, а со станции) и вдруг увидим, что наша Земля не шар, а тор. На рис.2 показан подлинный снимок Земли из космоса. Как будем жить на такой Земле? Как проведём меридианы и параллели? Как будет меняться сила тяжести в разных точках планеты? Как будет летать Луна? Будут ли приливы в океанах и как будет меняться атмосферное давление в разных точках Земли? А рассветы и закаты, как они будут выглядеть, ведь тор будет отбрасывать тень одной частью на другую? Как будет выглядеть глобус и географические карты?. Особенно политические, ведь на торе для раскраски карты надо не менее 7 красок, на плоскости, как известно, достаточно четырёх. На рис.3 показана попытка получения глобуса. А как будет выглядеть кратчайшая линия между двумя пунктами? Где лучше располагать передающие антенны для максимального охвата? Куда показывает компас?

Это подлинный вид Земли из Космоса

Такие должны быть глобусы

На шаре всегда есть точка, в которой нет ветра, или, другими словами, волосатый шар нельзя причесать гладко, всегда будет макушка, в которой волосы торчат пучком. А волосатый тор причесать можно – и вдоль, и поперёк, и под любым углом. Это свойство  отразится на метеорологических процессах на торообразной Земле.

Если вдруг торообразная Земля столкнется с огромным астероидом, то есть вероятность, что он пролетит в «дырку»…

Устали от путешествий? Вернёмся на нашу привычную Землю и ответим на последние три вопроса. Первый лёгкий: как разрезать тор двумя плоскостями, чтобы получить наибольшее число кусочков? Второй, ещё легче: как делают бублики без следов стыка? Третий самый сложный: на тор (например, камеру от колеса) наклеим две полоски – вдоль большой и вдоль малой окружностей так, чтобы они были зацеплены. Потом проделаем дырочку и через неё вывернем тор наизнанку. Теперь наши полоски окажутся не зацепленными, что противоречит закону, по которому нельзя расцепить два кольца, не разорвав их. Сомневающиеся могут сшить тор из старого чулка, наметать разноцветными нитками два кольца, вывернуть и убедиться в крушении основ математики.

Для тех, у кого нет старого чулка, предлагаем набрать в Turbo Pascal’e программу, рисующую на экране тор и поэкспериментировать с ней.


PROGRAM tor;
USES GRAPH,DOS,CRT;
CONST
R=180 ; RR=40 ; {радиусы большой и малой окружностей}
VAR
Fi,X,X1,Y,Y1,M,A,T :  INTEGER;
Hi,Q,W,U,V,Z,B,R1: REAL;
C: CHAR;
GraphDriver : Integer;
GraphMode: Integer;
BEGIN
GraphDriver:= Detect;
InitGraph(GraphDriver,GraphMode,'');
FOR Fi:=0 TO 360 DO BEGIN   {цикл по большой окружности}
FOR A:=0 TO 360 DO BEGIN    {цикл по малой окружности}
    Hi:=Fi*Pi/180 ;
    B:=A*Pi/180 ;
    R1:=R + RR * COS( B ) ;
    W:=R1 * COS(1*Hi) ;        {1}
    Q:=R1 * SIN(1*Hi) ;         {2}
    Z:= RR * SIN( B ) ; {+50*cos(4*Hi) ;}  {3}
    X:=TRUNC(300+1*(W-Q*COS(PI/3)));
    Y:=TRUNC(250+1*(Q*SIN(PI/3)+Z));
    IF A > 0 THEN LINE(X,Y,X1,Y1);
    X1:=X ; Y1:=Y;
    SETCOLOR(TRUNC((ABS(A) DIV 14 ) MOD(5)+10)); {выбор цвета}
  END ;
 END ;
 C:=READKEY;
 END.

Если в строках 1 и 2 заменить множитель при Hi на какое либо целое число и в строке 3 убрать фигурные скобки, то будет рисоваться тор, завязанный на узел самым невообразимым способом.

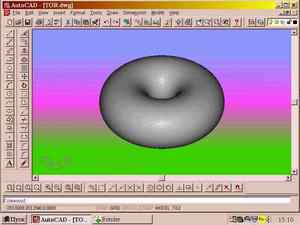
Для профессиональной работы с трёхмерными объектами используют специальные программы – AutoCAD и, конечно, 3D Sudio MAX. Торы, построенные с помощью этих программ, показаны на рис.4 и рис.5 соответственно. Ну вот и всё. В следующий раз кусая бублик или заклеивая камеру велосипедного колеса, отнеситесь к их форме с должным почтением

Дополнение вдогонку.

В Компьютерре №10/2000 было рассказано о торе, в том числе и о космической станции в виде тора, в которой за счет вращения создается сила тяжести. В связи с этим родилась задача: как, не выглядывая в окно, определить: сила тяжести в вашей комнате за счет гравитации или за счет центробежной силы от вращения станции?

Первым делом напрашивается маятник. Как будет меняться плоскость его качания на вращающейся станции? Как он будет качаться в плоскости вращения тора? Как мы отличим его от маятника Фуко?

Если мы подпрыгнем вертикально вверх, то на станции во время полета в прыжке сила тяжести на нас не действует, остается лишь линейная скорость касательная к тору и не совпадающая по направлению со скоростью пола в точке прыжка. Пол снова «подхватит» нас и мы, может, не заметим разницы с прыжком на Земле.

Как будет вести себя волчок?

Куда полетит воздушный шарик на станции?
Какие силы действуют на молекулы воздуха в комнате? Достаточно ли вращения для создания нормального атмосферного давления?

Если бежать против вращения станции со скоростью, равной линейной скорости станции, то можно обрести невесомость, а если в сторону вращения?
Подумайте и напишите, обсудим.