Зигзаги Александрова

Математика удивляет нас как видами самых разных формул, так и способами их преобразований. Например, существуют десятки, если не сотни, представлений числа ПИ в форме рядов, сумм и итераций. Автор давно увлекся задачей о золотом сечении, одним из решением которого является выражение [1+5^(1/2)]/2. Попытка обобщения столь частного результата привела к интересному исследованию

Конечную сумму: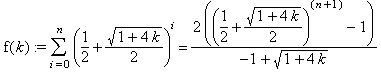

всегда можно привести к виду:

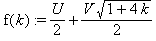
Здесь  k = 0 ,  1 ,  2 ,  …  ;  U   и  V  - целые положительные числа, зависящие от n и  k.

При k = 0  функция  f(0) = n + 1  и  представляет собой обычный натуральный ряд чисел. Однако, рассматривая случай  k = 1, автору удалось сделать неожиданно интересное открытие.

В самом деле, если  k = 1 , то:

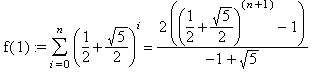
Заметим,  что    структуры 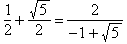   являются решениями задачи о золотом сечении.

Выполнив несложные, но громоздкие преобразования, можно получить  числа  U   и  V   для  любого  n. Составим таблицу начальных значений этих параметров:

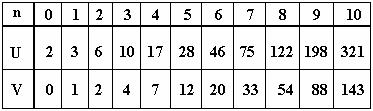
Как же продолжить ряды чисел U и V, не производя никаких вычислений? В математике известны примеры формального построения числовых последовательностей. Самый яркий среди них – биноминальные коэффициенты, которые находятся при помощи треугольника Паскаля.

После недолгих раздумий мне удалось разработать красивый прием, позволяющий определять сколь угодно длинные ряды чисел  U и V для  случая k = 1. Процедуру я скромно назвал зигзагами Александрова. Вот они:

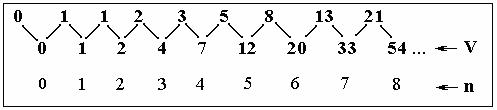
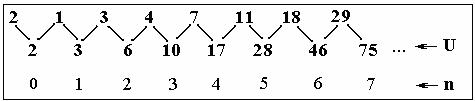
Верхняя строка чисел пилообразной конструкции – это простой ряд Фибоначчи, то есть такой ряд, в котором любой его член равен сумме двух предыдущих. Для коэффициента  V он классический и начинается с пары чисел  0  и  1.  Для коэффициента  же U ряд Фибоначчи начинается с пары  2  и  1 .  Числа, характеризующие V и U,  получаются  так. Самый первый член ряда совпадает с первым членом ряда Фибоначчи, а каждый последующий – это сумма предыдущего члена с ближайшим левым верхним числом зигзага.

Статья написана специально для arbuz.uz

Публикуется впервые.

Георгий Александров, 10 апреля 2006 г.

 

Примечание. О вариациях на тему рядов Фибоначчи можно прочесть в статье Кролики-каннибалы, четверостишия и заповедник последовательностей.