|
|
|
|
|
|
|
|
|
Ломтик со скатомСорок девятый ломтик. Срок девять - это наименьшее число такое, что оно само и его ближайшие соседи имеют среди делителей квадраты. Если знаете еще интересные свойства этого числа - пишите, прославитесь - обещаю. А название ломтику дала флешка со скатом, присланная арбузником Sepulka - подвигайте курсор, только осторожно...
Еще более потрясающая флэшка - на http://www.nobodyhere.com/ человек живет полной насыщенной жизнью. Спасибо за подсказку известному арбузнику E'zy,
Эту открытку прислала знакомая, занимающаяся проектированием обработки сложных поверхностей на станках с ЧПУ в системе Unigraphics. В ней (системе) столько волнующих возможностей для проектирования поверхностей - 3D Max и прочие с завистью отдыхают.
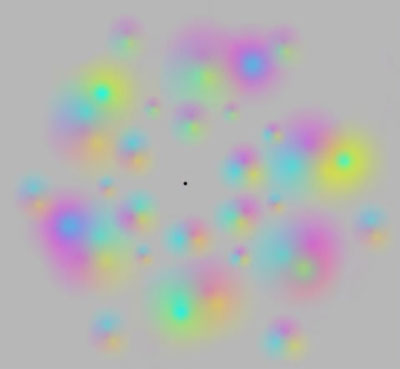
Знакомые прислали оптическую иллюзию - якобы если смотреть нв черную точку, то цветные пятна вскоре исчезнут. У меня не исчезли... Помните, что говорят о тех, кто не видит иллюзии? (В прошлом ломтике было...) То-то и оно..
Несколько задач для разминки Задачка для школьников, поступающих в 8-й класс одной школы: Петя и Вася вместе обычно
выпивают бидон молока за 12 минут. Но после восьми минут Петя заснул, а Вася допивал остаток еще 7 минут. За сколько
минут выпивают бидон отдельно Петя и
отдельно Вася?
Задача от Я.И. Перельмана. На пятерку решать без икса и устно. Продавец продает шапку. Стоит 10 р. Подходит
покупатель, меряет и согласен взять, но у него есть только 25 р. Продавец
отсылает мальчика с этими 25 р. к соседке разменять. Мальчик прибегает и
отдает 10+10+5.
На столе стоит стакан, в стакан можно наливать воду. Если
стакан пуст, центр тяжести находится ровно на половине высоты стакана...
Если стакан полон до краёв, центр тяжести находится также ровно на половине
высоты стакана. И еще в том же комюнити Задача отличная задача Прислали 2 палиндрома: Ужас! Ангел лег на сажу! А год-то хот-дога
Программа на VB рисующая фигуры Лиссажу. Очень
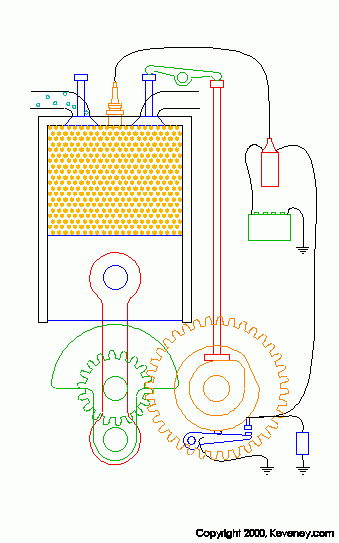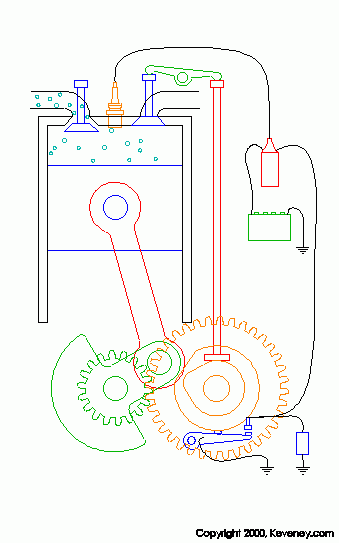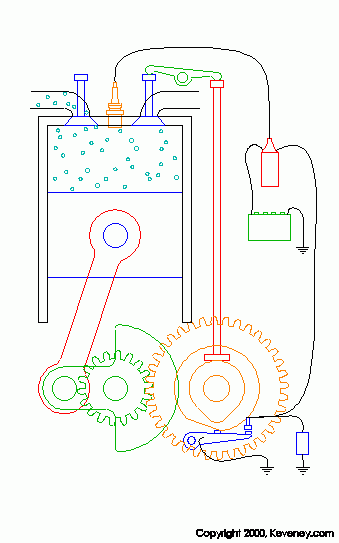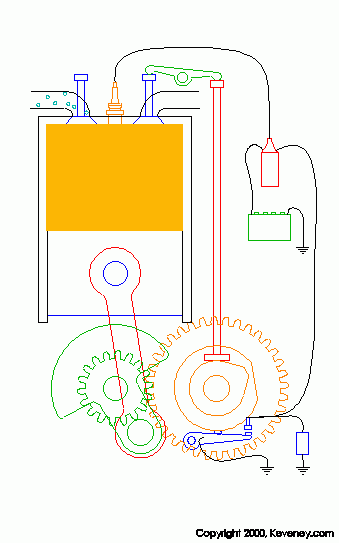
красиво. Прислал Pro[)!9y. На странице http://www.keveney.com/Engines.html собраны отличные илюстрации по работе двигателей, например, такая:
Так и просится добавить звук работающего двигателя... - отличное пособие. Некоторые ссылки: 1. Болгарский сайт с занимательными флешками www.zairgavka.com 2. Книги Перельмана http://eqworld.ipmnet.ru/ru/pastime/puzzles.htm 3. Забавный сайт со смешными рисунками "Крыльев нет" http://www.kryliev.net/ 4. Гипердвигатель перенесёт корабль в параллельные Вселенные http://www.membrana.ru/print.html?1136912940 5. Алферов С.А. Вписанно-описанные прямоугольники, трансцендентный квадрат и пропорции человека 6. Антология древнерусской литературы 7. Посмотри коллекцию минералов - очень интересно! 8. Кунсткамера Химические рекорды
9. Якоб Нильсен рассказывает о том, как Кривые Зипфа описывают распределение посетителей, приходящих на ваш сайт по ссылкам с других сайтов
10. Галерея художницы Татьяны Кугай. Посмотрите какие картины! Одна из них (с арбузным ломтиком) была в прошлом ломтике. 11. Портал интеллектуальных развлечений, в том числе много оптических иллюзий. 12. Всемирная паутина меняет геном человека, утверждают учёные.
13. Обязательно рассмотрите стол, изображенный на
http://www.livejournal.com/users/ca 14. Посмотрите заставку к сайту Deadfish animation — виртуальная студия Маши Якушиной! Дизайнер - Владимир Липка, все его работы - непременно чудо, непременно радость, запомните это имя. 15. Конструктор из Лего собирает Кубик Рубика, представляете? Это тут http://www.toster.ru/44/
16. Отличная забава -
http://files.deviantart.com/f/2004/1 17. Интересный сайт про числовую спираль - я так и не разобрался в принципе ее построения... (на английском) 18. Статья о фракталах вошла в число избранных статей русской Википедии. 19. Знакомый Борис рассказал о ташкентском художнике-карикатуристе, вот один из его рисунков
Фото прислал Анатолий ака kikaxa известный, в частности тем, что в свой ЖЖ не пишет, только комментирует френдов
Георгий Александров прислал стишок, позволяющий запомнить число Пи Раз у Коли и Арины И для запоминания числа "е" Мы порхали
Вопрос от Александра Каминского: По трем проекциям представить тело - для примера на первых трех картинках шар, куб и цилиндр. А что на четвертом?
Рекорд с чистого листа: бумага сдаётся 12 раз
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
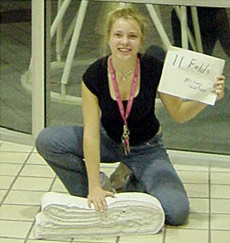
Мировая рекордсменка Бритни Гэлливан и бумажная лента, сложенная вдвое (в одном направлении) 11 раз (фото с сайта mathworld.wolfram.com). |
Кажется, тут-то мы начинаем понимать, откуда берётся известное многим ограничение на 7 или 8 раз (ещё раз – бумага у нас реальная, она не тянется до бесконечности и не рвётся, а порвётся – это уже не складывание). И всё же…
В 2001 году одна американская школьница решила вплотную заняться проблемой двойного складывания, а получилось из этого целое научное исследование, да ещё и мировой рекорд.
Собственно, началось всё с вызова, брошенного педагогом ученикам: "А вот попробуйте сложить хоть что-нибудь пополам 12 раз!". Мол, убедитесь, что это из разряда совершенно невозможного.
Бритни Гэлливан (Britney Gallivan) (заметим, сейчас она уже студентка) поначалу отреагировала как Алиса Льюиса Кэрролла: "Бесполезно и пробовать". Но ведь говорила Алисе Королева: "Осмелюсь сказать, что у вас не было большой практики".
Вот Гэлливан и занялась практикой. Порядком намучившись с разными предметами, она сложила-таки лист золотой фольги вдвое 12 раз, чем посрамила своего преподавателя.
 |
|
|
На этом девушка не успокоилась. В декабре 2001 года она создала математическую теорию (ну, или математическое обоснование) процесса двойного складывания, а в январе 2002 года проделала 12-кратное складывание пополам с бумагой, используя ряд правил и несколько направлений складывания (для любителей математики, несколько подробнее — тут).
Бритни заметила, что к этой проблеме ранее уже обращались математики, но правильного и проверенного практикой решения задачи ещё никто не предоставлял.
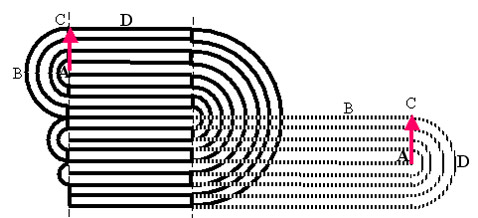
Гэлливан стала первым человеком, который правильно понял и обосновал причину ограничений на сложение. Она изучила накапливающиеся при складывании реального листа эффекты и "потерю" бумаги (да и любого иного материала) на сам сгиб. Она получила уравнения для предела складывания, для любых исходных параметров листа. Вот они.
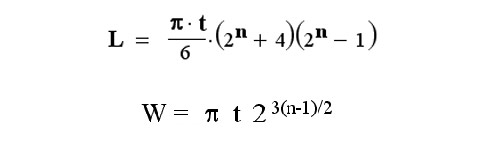
Первое уравнение относится к складыванию полосы только в одном направлении. L — минимально возможная длина материала, t – толщина листа, и n — число выполненных сгибов в два раза. Разумеется, L и t должны быть выражены в одних и тех же единицах.
Во втором уравнении речь идёт о складывании в
различных, переменных, направлениях (но всё равно – вдвое каждый раз).
Здесь W – ширина квадратного листа. Точное уравнение для складывания в
"альтернативных" направлениях – более сложное, но здесь приводится
форма, дающая очень близкий к реальности результат.

Гэлливан и её рекорд (фото с сайта pomonahistorical.org).
Для бумаги, которая не является квадратом, вышеупомянутое уравнение всё ещё даёт весьма точный предел. Если бумага, скажем, имеет пропорции 2 к 1 (по длине и ширине), легко сообразить, что нужно сложить её один раз и "привести" к квадрату двойной толщины, а затем воспользоваться вышеупомянутой формулой, мысленно держа в уме одно лишнее складывание.
В своей работе школьница определила строгие правила двойного сложения. Например, у листа, который свёрнут n раз, 2n уникальных слоёв обязаны лежать подряд на одной линии. Секции листа, не удовлетворяющие этому критерию, не могут считаться как часть свёрнутой пачки.
Так вот Бритни и стала первым в мире человеком, сложившим лист бумаги вдвое 9, 10, 11 и 12 раз. Можно сказать, не без помощи математики.
Смайлики от Мегафона
| Вот маленькие превьюшки всей серии смайликов для Мегафона
48х48 в натуральную величину здесь: |
||||||
| http://www.livejournal.com/community/ru_icons/290452.html?mode=reply | ||||||
Источник - АКАДЕМИЯ ТРИНИТАРИЗМА
Наглядно изменчивость воды продемонстрировал японский исследователь Масару Эмото — выпускник университета в Иокогаме и доктор наук по проблемам альтернативной медицины в двух томах своей книги «Послания воды». Доктор Эмото провел исследования, в ходе которых он замораживал капельку воды, а потом — при температуре -5 градусов — рассматривал образовавшиеся кристаллы под микроскопом и фотографировал их встроенной в микроскоп фотокамерой. Подвергая воду различным воздействиям, он снова ее замораживал, фотографировал и сравнивал изменения.
Наиболее рельефно эти изменения видны после того, как вода «прослушивает» музыку. Самые красивые кристаллы образуются под воздействием классики. Менее эффектные, но тоже гармоничные дает народная музыка. И уж совсем безобразная «грязь» остается от музыки в стиле «тяжелого металла».
Оказалось, что молекулярную структуру воды меняют вибрации человеческой энергии, мыслей слов, идей и звуков.
Необходимо принять во внимание то, что вода после воздействия замораживается в кристаллы льда, но как меняется физическая структура льда! Это заставляет нас подумать и представить, что то же самое происходит и с водой внутри нашего организма!
Вы можете посмотреть презентацию результатов исследования чудесных свойств воды
Несколько арбузных фоток, случайно найденных в Сети






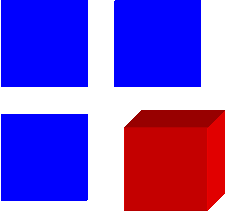
Чем отличаются эти две картинки?


Скульптур-мультур

Подходи народ...

Пока наверное все..
| Автор | )c( 2000-2019 Kопирайта нет, копируйте на здоровье :) 100112 лет в Интернете |
|