Ломтик накопительный

В том смысле накопительный, что накопилось много ссылок и материалов, которые надо обозреть, а то они забудутся или заслоняться более свежими. Напоминаю, что выходят Арбузные ломтики по средам на Информационном Буме. Взгляните - как на приложение к этим "настоящим" арбузным ломтикам.

Сороковой, почти юбилейный, выпуск газеты-ломтика, 40 - интересно лишь тем, что это максимальное число сфер, касающихся каждой сферы при плотнейшей упаковке их в пятимерном пространстве. Плюс - количество расстановок 7 ферзей на доске 7*7 не угрожающих друг другу. Много интересных сведений о сорока, в том числе и поговорок, найдете в статье Колесо Юпитера в главе " Сорок кадушек соленых лягушек ". Кто знает еще интересные свойства номеров газет - сообщайте в Форум или мылом.

Еще хочу обратить внимание посетителей, что с апреля регулярно выходят Арбузные корки, архив которых можно рассматривать как один все время пополняемый ломтик

Итак, картинка ломтика
 

Просто чудо! Учитывая давнюю привязанность Арбуза к пузырям и прочим поверхностям. Из галереи Джона Салливана ( John M. Sullivan) , посмотрите и другие работы.

 
напоминаю -  разделитель тем еще и
ссылка на Форум для обсуждения ломтика

Главная новость сайта - выложены фракталы Курликю, вот самый любимый:

И еще новость: подавляюще число посетителей заходят на Угадыватель мыслей. Так вот, запущен еще более таинственный Угадыватель №2, как он работает - мистика просто!

Смотрите галерею "Красота хаоса" о построителе аттракторов.
 

 И ссылка на интересную страницу Джорджа Харта, посвященную геометрическим моделям. Когда-то у моих детей был конструктор - набор из сцепляемых прямоугольников, можно было строить не только многогранники, но и поверхность, на которой выполняется геометрия Лобачевского, вводя в каждую вершину по три семиугольника, например. Правда, она пыталась "вздыпупиться" и самопересечься, но путешествовать по ней было возможно.

После публикации японской странички с вырезанными из арбуза произведениями искусства я получил много писем с ссылкой на нее, и они продолжают приходить. Всем спасибо, я уже знаю о ней :)

А вот фотография, присланная арбузником с ником novosel - так в Турции развлекаются в свободное время повара

И еще от него же



 

А теперь арбузный тигр

сфотографированный арбузником из Амурской области. Вот фрагменты из его писем:

Здравствуйте!
Пишу Вам я, Владимир, почитатель вашего сайта и всех ваших трудов.
Попал я на Ваш сайт со странички "Русский Проект" http://rusproject.narod.ru/  и просидел на Вашем ресурсе весь счёт... Заработал немного денег, оплатил несколько часов и за один раз(!) просадил их все на Арбузе... Интернет у нас тут слабенький - 1кБ/с, но всегда когда я оживляю модем я точно знаю, куда я зайду в первую очередь:)
Я сам имею ресурс в сети, даже с немного похожей с Арбузом по направленности http://web-svalka.narod.ru/
Он не раскрученный и вообще мне с моими запредельными вэб-скоростями можно только мечтать о хорошем состоянии сайта, но наступит время и Вы меня похлопаете по плечу и скажете: "Молодец, теперь я знаю - дело не пропадёт!"

Действительно, Ваш ресурс - особенный, мне даже иногда кажется, что я не сижу на советском деревянном стуле, а гуляю между фракталов, паутиноидов. Я поражаюсь - Вы так умело справились с дизайном, что даже какие-то левые на первый взгляд картинки так вливаются в общий контекст, что именно без них получился бы совершенно другой сайт. Всегда есть что почитать, а галерея кнопок меня вообще приятно удивила: простые 88x31, но без ссылок и всякой коммерции уже не надоедливые баннеры, которые мой проводник игнорирует, а самая, что ни есть, картинная галерея! Благодарю Вас за идеи и неунывание! Немного ударюсь в критику и скажу, что в офф-лайне просматривать сайт нельзя, а очень жаль, ведь таких как я много и приходиться выкручиваться. Пожалуйста, сделайте сайт, который можно глядеть не даря деньги провайдеру! Хотя на Ваш ресурс никаких денег не жалко!

Вообще-то, мои друзья и близкие не понимают Арбузного творения, они считают неинтересными статьи с этого сайта, но мне всё равно, я не предам Арбуз!!!

Попал на арбузный сайт я совершенно случайно, просто заметил на "русском проекте" (а я занимаюсь кодингом на ВБ и поэтому являюсь частым посетителем этого сайта) ссылку на ваш сайт в разделе "арбуз" (сначала я туда и не собирался - ну при чём тут арбуз???), а потом открыл для себя целый новый мир!

Гулять по сайту мне не столь интересно, сколь интересно скачивать и разглядывать потом в офф-лайне Арбузную газету. Ваша газета как киндер-сюрприз: что внутри не знаешь, но что будет интересно - это точно, а винегрет из разных материалов настолько увлекает, что забываешь обо всём на свете; а когда заходишь в раздел на сайте, точно знаешь что там будет (ну, есть, конечно, некоторые исключения:) Конечно, это не моё
собачье дело, но почему бы вашему сайту не обзавестись рассылкой? Я бы писал кипятком и какал гвоздями от радости!

Игра жизнь показывает эволюцию алфавита: ставим глайдер и запускаем (он у меня не перемещается, а растёт). Постепенно появляются о, ф, н, х, ж, э вместе с е и т. д. Иногда можно увидеть целые фразы, а одно поколение мне вообще напомнило послание, которые составили астрономы из двоичного кода, которое содержало некоторые математические, физические и биологические данные о Человечестве на Земле (число, атомы, АДН /спираль ДНК/, население Земли, человеческие существа и телескоп Аресибо). Кстати, была программа по ОРТ про это послание (я очень жалею, что не посмотрел), а в рекламе видел, что был получен точно также составленный ответ, только на поле. Вы имеете про это информацию? Да, а почему на арбузе нет
этой программки - игры жизнь, про которую так много написано?! У меня есть небольшая программка, но моя "жизнь" не та "жизнь", которая нужна... Моя "жизнь" отстой, я её ненавижу:)

А вы увлекаетесь демосценой? Ясно, что нет, так как в демках совмещены поэзия и математические красивости, музыка и музыка математики... На моём сайте в 5 и 6 номерах журнала есть две прекрасные демки, настолько маленькие и живописные, что
оторваться нельзя. Мой сайт тут: http://web-svalka.narod.ru/  Также могу посоветовать сайт клевейших демо-мейкеров: http://ithaqua.stravaganza.org  Моя поистине скромная кладовка насчитывает 38 демок... Это очень мало... Интернет в нашей местности не позволяет: 1кБ/с... Так что новелла Галины Ни "Планета справедливости" рассказывает об утопии... 100мБ на семью в неделю... Да мне столько и за всё время юзанья не снилось!!!
Ага, также ищите демку MACRONAUT (возможно есть на сайтах http://toxi.co.uk и http://lateral.net). Ну просто очень захватывающе!
 

  И еще отрывки из полученных писем.

Здравствуйте Евгений,
Возвращаясь к статье про часы хочу дать вам одну интересную ссылку:
http://www.tvkultura.ru/news.html?id=5930&cid=1004
Вот еще несколько сайтов на мой взгляд интересных для Вас.
http://www.mrwong.de/myhouse/
Построй свой этаж в виртуальной Вавилонской башне
Ресурсы, посвященные анимации.
www.reclani.tele-kom.ru  сайт любителей анимации.
www.kinoart.ru
www.vinci.ru  Мир Леонардо .
Жду новых публикаций на ARBUзе
Спасибо за Ваш сайт.Читаю регулярно , жаль обновляется редко.
Вячеслав, Санкт - Петербург

Сергей, выпустивший арбузоидов на свободу, и нашедший арбуз без косточек, заметил также

необъяснимое появление диагоналей... вы их видите?

Вдруг обнаружился тезка http://arbuz.de!!! Вот что пишет его автор:

Добрый день, Евгений!
Вот так могут отличаться друг от друга разные сорта арбузов ;-)
Мой арбуз появился в результате месячной работы год назад, и с тех пор мало чем изменился. Делал я его как источник разнообразной полезной информации для проживающих в Германии русских переселенцев по принципу - как можно проще и доступнее. Для меня вопрос почему арбуз? имеет кроме ответов потому, что слово на а, короткое, запоминающееся, потому что арбуз вкусный и полезный, ещё и некоторые личные предпосылки, - поскольку я тоже родом из арбузного края. Поддержка этого сайта отнимает у меня совсем немного времени, поскольку, после того как он был проиндексирован, на него посетители пошли сами без каких бы то ни было моих усилий (ежедневно 40-50 человек). Корректировки и дополнения в справочный отдел приходят почти каждый день, но это отнимает всего несколько минут в день. Короче, сайт такой же нетребовательный и жизнестойкий, как арбуз. Все предложения по размещению на нём рекламы я отклоняю.

Есть ещё много идей, но большинство из них чрезвычайно сложны в реализации. Наиболее интересной идее уже 4 года - практически столько же я за компьютером,- но пока ещё уровень моих компьютерных знаний не достиг того уровня, чтобы вплотную заняться её реализацией. Эта идея - интеллектуальная поисковая машина, над таковой работают уже многие коллективы, но у всех у них другие принципы реализации. Кстати, последняя статья на эту тему в Internet Zone - http://www.computerra.ru/think/sentinel/36049/

Приятно было познакомиться, Евгений,
сайт у Вас замечательный, я ещё не раз приду почитать.

Фрагменты из писем Людмилы Орловой

Уважаемый Евгений! У меня есть к Вам предложение. Я-любитель, моё хобби - теология. И как всякий любитель мечтаю стать профессионалом. Едва выйдя в Интернет, я тут же нашла искомое - журнал Арбуз Ваши поиски тайны жизни на Земле близки к моим. Только я искала их в течение 2-3 лет в следующих местах: Библия, Махабхарата, Шри Ауробиндо,Рерих, Блаватская, Даниил Андреев. Перемолов море информации, я сделала несколько выводов, которые могут быть Вам интересны. И если это окажется так, прошу помочь мне, я человек далекий от математики, информатики, физики и т.д. Хотя, имея высшее железобетонное образование, я могу и хочу воспользоваться вашими наработками, которые выглядят вроде бы игрушками, а на самом деле куда более серьезны. Для начала сообщу Вам, если вы не занимались изучением сознания, следующее. Существует материя сознания. Её индийское название - мулапракрити. Она недискретна наполняет вселенную не имеет пространственных и временных характеристик называется тьмой, бездной, ну, в общем, ужас, ничто. Её называют в Библии землей. Если её поместить в замкнутое силовое поле, например, внутрь формы Лиссажу, она начинает менять свойства приобретает текучесть, в силовом поле проявляющееся как циркуляция. Из земли получается глина. Из глины - вода. Итогом агрегатных превращений является воздух. Еще раз подчеркну, что это только условные названия состояния материи сознания. Мною понято, что история развития жизни на Земле, описанная практически во всех религиозных писаниях, сводится к постепенному развитию силовых полей, в которых развиваются организмы и, в конечном итоге, человек. Для произрастания чего-либо стоящего в землю следует кинуть семя. Это семя изображалось точкой в круге. Точка для наблюдателя выглядит как луч света, описывающий круговую траекторию Естественно, на некотором расстоянии от луча возникнет круговой циркуляционный поток, превращающий землю в глину. Обычное синусоидальное колебание из центрального источника в векторной системе координат нарисует нам восьмерку. Векторное исследование даст нам понимание, что в одной половине этого поля вектор воздействия на материю сознания направлен от центра наружу(действительная часть), в другой половине - от периферии восьмерки к центру(мнимая часть). Инь и ян. Непременным условием понимания фаз колебаний является их возврат - эхо от точки 2пи. От 0 до пи - день, от пи до 2 пи - ночь, и обратно от 2 пи до пи - вечер, от пи до 0 - утро. Если же мы допустим, что колебаний два - взаимно перпендикулярных (Адам и Ева), то мы получим более интересные образования. При разности амплитуд и частот увидим "цветочки", листики, бабочки, при отношении частот ? - векторная диаграмма выявит шестилепестковый лотос, три лепестка - действительные, три - мнимые. Это образование называется "корень жизни" и является питательным корнем для роста сознания животной жизни на земле. Из этого лотоса выходит бог Вишну. Если интересно нарисовать график, мы увидим контуры женских грудей, между которыми фаллос весьма ударной формы. При фазовом сдвиге колебаний Евы, ну хотя бы на 1/8 пи, происходит сотворение трех измерений буквально на глазах. Фигура Лиссажу превращается в трехмерное тело, которое возле центра опишет эллипсоид, эквивалентный земному шарику, и , в частности, ауре человека. В Махабхарате у одного царя было два сына - зрячий и слепой. Жена зрячего родила пять сыновей, а у слепого (сдвиг по фазе) - жена долго носила в животе странный, холодный шар. Когда она его выродила, мудрец сказал ей: разбей шар на кусочки и посади кусочки в землю, и у тебя вырастет сто отличных сыновей. Все дело в черепахе, говаривал Конфуций. Если внимательно посмотреть на график колебаний, можно увидеть черепаху с хвостиком… Конечно, шарик описывается как один из случаев овалов Кассини. Ну, а в центре Земли, там, откуда бьет нам в глаза точка света, что там? Вывернем шар наизнанку через центр. Я люблю интуитивно-сенсорное восприятие, поэтому, пройдя через центр, я вывернусь в шар четвертого измерения - тор. Причем свет, который я видела перед глазами в вывернутом состоянии, оказывается вокруг меня! Больше того, он как лампа горит внутри меня. С появлением фазового сдвига перестанем думать о существовании мнимой части колебаний. Пусть она останется в земле. Теперь опереться в рассуждениях можно не на синусоиду, а циклоиду. Нарисованная в определенных параметрах, она даст нам объяснение биения нашего сердца. Это исследование в статье "Улитки Паскаля" Только животные сердца и человеческие разнятся. Например, Навуходоносору, когда он зазнался, дали сердце быка, а когда покаялся - вернули в человеческий вид. Точка "выверта" мне, как теплотехнику, являет сопло, в котором закачанная в лотос и растопленная в глину земля подвергается изменению агрегатного состояния. Со свистом пролетая в трубу одного из апокалиптических ангелов, она превращается в пар, который согласно первой (или второй?) странице библейских текстов "орошает лице земли". В духовном строении человека этот узел перехода из третьего в четвертое измерения соответствует пупку, солнечной чакре. Теперь, учитывая, что Адам и Ева разнятся, мы увидим перед глазами уже не точку света, а целое светило, которое, если мы оседлаем один из векторов и пройдем день и ночь, последовательно принимает то диаметр побольше, то поменьше (читайте про светила на четвертый день творения). Не знаю, как пар конденсируется, убейте, но превращается материя сознания в воду, чистую как слеза, не окрашенную информацией материю сознания. Этой водой крестил иудеев Иоанн-креститель, смывая ею всю чушь в сердцах фарисеев. Представителем человечества, в совершенстве овладевшим информационным воздействием на материю сознания вода является Илия, в духе и силе его родился уже упомянутый мной Иоанн… И тут я вплотную подхожу к Вашим игрушкам, Евгений! Дальше то что? Известен нам потоп, известен ковчег, известно также, что некоторые горе-cтроители, понаделав из глины кирпичей, обожгли их огнем и начали строить вавилонскую башню. Эту башню, как неудачную попытку сознания Земли вывернуться в очередной раз, я благодарностью сообщаю) увидела у Вас. Это фигура Лиссажу, которая имеет кодик xx= rr*(sin(0.995*v)+0.6*cos(2#*v))+xmax/2 yy= rr*(cos(1/005*v)+0.5*sin(15.075*v))+ymax/2 Предыдущая фигура, описанная Вами как "безумие", как я сильно подозреваю, является тем самым быком - Навуходоносором, которое вполне может превратиться в нечто более приличное. Но как? Библия рассказывает нам, что завет Бога с Авраамом был таким: отец народов должен был рассечь быка пополам, а между этими половинками Бог воспламенил землю. Как бы там ни было, Авраам вывернулся удачно. Вместе с ним и сознание Земли. Достигли этого иудеи, бродившие по пустыне 40 лет, разбившиеся на 12 колен. Момент выверта из тора четвертого измерения в пятое измерение, которое я называю разумом произошел при взятии Иерихона. Если не знаете или не помните, шесть дней иудеи обходили городмолча. На седьмой день они обошли город семь раз и дружно заорали. Это был звуковой прорыв сознания в удивительную фигуру, которую я Вам посылаю в файле вместе с письмом. Сопел в нём<br> четыре. В них происходит изменение агрегатного состояния воды в воздух. В индийских духовных традициях это называется акаша. В акаше, в отличие от воды, куда более легка информационная эволюция сборища двуруких и одноголовых. Человек, наконец, стал разумным. Если взять одну из интересных картинок овалов Кассини, собранных Вами в "Арбузе", то мы увидим наши глаза ( потом и уши и нос). Трехмерный продукт этого силового поля является нашими глазными яблоками, а само поле четырехмерно. Естественно! Мы бы не могли видеть трехмерные объекты! Ной, например, видел предметы плоскими. Точкой перехода в пятое измерение разума является "третий глаз", межбровье, или в индийской духовной науке о чакрах - "аджна". Увидеть Землю из пятого измерения трудно. Я могу похвастаться, что видела. Это действительно тор. Но выглядит он не как поверхность планеты в морях и облаках. Он составлен из светящихся точек, как звездная туманность тороидальной формы, каждая звезда - это человек, вернее, светящееся сопло для материи сознания каждого отдельно взятого человека. Что дальше? Дальше был Христос. Ему потребовалось три дня быть в центре Земли… И Он пришел к Творцу. Вывернулся ещё раз? Кстати, это небезопасные штуки. Я сильно подозреваю, что разница между Ним и нами (непорочное зачатие) не даёт нам возможности повторить его путь. Мешает этот чертов Вавилон. Как Вы уже поняли, он еще никуда не делся с Земли и развивается своим, неуследимым пока методом. В Библии эта тварь вырастает в дракона с семью головами и десятью рогами. Но каждый родившийся чем-то энергетически с ним связан. Эта загвоздка находится в физическом теле. Мне, например, совершенно не удается сенсорно - интуитивным восприятием добиться понимания модели построения земного шара с его гравитационным и электромагнитным полями. Может это просто от лени? Мало того, что Вавилон мешает развитию сознания, он просто убийца. Например, если я захочу вывернуться из разума пятого измерения в шестое, мое сознание просто "хлопнется", я могу потерять разум, как согрешившая Ева, а ещё хуже - сердце, как Каин, убивший Авеля. Впрочем, это опять история Навуходоносора… Впрочем, утешает то, что еще один завет от Бога состоял в обрезании крайней плоти на восьмой день. ...........

Желающим продолжить эзотерическое общение могу выслать адрес Людмилы, а если есть предложения насчет алгоритмов всяких поверхностей, то пишите мне или в Форум.

Драгоценные камни Арбузные турмалины, ссылку прислал "тот самый" Рей Гирван, английский публицист, собравший полнейшую коллекцию ссылок на ресурсы по занимательной математике. Кстати, Арбуз в ней на первом месте, так как добавлен последним :) Еще Гирван прислал ссылки на мировые рекорды, связанные с арбузами.






Еще рекомендую ссылки:

Цифровые стихи на сайте с характерным названием "Розовые слоники бегают по комнате, бегают и прыгают, сволочи ушастые".

http://www.0x800ccc0d.com/ - адрес соответствует содержанию

Набор программ с отражением от сфер...

СНЫ БЕССОЗНАТЕЛЬНОЙ БАБОЧКИ или О СВОБОДЕ ИНТЕРНЕТ ПЕРЕПИСКИ
Кстати, это на проекте Ольги Таевской, о ней, о ее знаменитом муже и братьях читайте в моей колонке Поучительный квартет сетевого бытия.

И всех интересующихся обучением дошкольников математике и вообще интересными педагогическими находками, прошу посмотреть "В гостях у Марии"

Институт исследования природы времени, посмотрите сколько всего интересного!

Отличная программа для развития памяти, очень рекомендую

Источник. Особенно приятна игрушка для отдыха - невозможно оторваться! Я все-таки победил ее! Попробуйте, не пожалеете!





 

Если вам надо решить задачу по геометрии, то вы попали куда надо! Сайт, посвященный решению геометрических задач!
 

По какому времени мы живем - статья на Астронет

Шутки и ошибки в учебнике по математике

Лучшие научно-популярные сайты, список на Мембране-ру

Феликс Кривин. Научные сказки

Здесь каждый день выкладывается интересное фото природного явления.

Виртуальная энциклопедия Казахстана Александра Ляхова, заочного знакомого.

Черный квадрат Рунета

История жизни и смерти Э.Галуа

В мае появилось следующее сообщение.

Сооб: 601 из 618 +606                                                      RU.AI
От  : Yury V. Reshetov                          2:5085/131.6 Tue 11 May 04 16:43
Кому: All
Тема: Теорема Геделя о "неполноте" формальных арифметик опровергнута
                           И H Ф О Р М А Ц И О H H О Е

                                С О О Б Щ Е H И Е

Опpовеpгнута Втоpая теоpема Геделя о "неполноте" фоpмальных аpифметик. В связи
с этим, также теpяют смысл еще две теоpемы: Таpского о пpотивоpечивости
интеpпpетаций ФА и Чеpча о неpазpешимости пpедикатов пеpвого поpядка. Последняя
теоpема  pанее была попpавлена в стоpону частичной pазpешимости.

В качестве опpовеpжения пpиводится pеализация алгоpитма фоpмальной аpифметики
не обладающей вышепpиведенными недостатками, а также описание допущенной
Геделем ошибки в последней части доказательства.

Для тех, кто не в куpсе, о чем идет pечь, выдеpжки из "Математическая логика"
А.H. Колмогоpова и А. Г. Дpагалина. М.: МГУ, 1984 :

--------------------- Hачало цитаты -----------------------------------

"Знаменитая вторая теорема Геделя, полученная в тридцатых годах XX века,
утверждает, коротко говоря, что непротиворечивость достаточно богатой теории не
может быть установлена средствами самой теории. Этот факт побуждает
специалистов по основаниям математики изыскивать математические методы, с одной
стороны, убедительные (с той или иной точки зрения) и, с другой стороны, не
входящие в теорию, непротиворечивость которой изучается. Очень многие
исследования по неклассическим, модальным и интуиционистским логикам
стимулированы этой идеей.

Можно сказать, что к настоящему времени непротиворечивость таких теорий, как
элементарная геометрия, арифметика, анализ, хорошо изучена и достаточно надежно
обоснована. Hепротиворечивость мощных аксиоматических теорий множеств, таких
как система Цермело-Френкеля или теория Куайна, гораздо более проблематична.

Большой интерес представляет изучение полноты той или иной теории. Во многих
математических теориях время от времени возникают конкретные проблемы, которые
не удается ни доказать, ни опровергнуть. Иногда это бывает в силу технической
сложности самой проблемы, и, спустя определенное время, проблему все же удается
разрешить. Однако в некоторых случаях ситуация совершенно иная: проблему просто
невозможно ни доказать, ни опровергнуть в рамках исследуемой теории. Так, было
показано, что подобными проблемами в теории множеств Цермело-Френкеля являются
континуум-проблема Кантора и многие другие важные теоретико-множественные
проблемы. Подчеркнем, что дано было точное доказательство того факта, что,
например, аксиома выбора не может быть ни доказана, ни опровергнута в теории
Цермело-Френкеля. Теорема Геделя о неполноте утверждает, что всякая достаточно
богатая теория необходимо содержит утверждения, которые нельзя ни доказать, ни
опровергнуть в рамках теории.

Тем не менее некоторые важные теории оказываются полными. Таковы, например,
элементарная геометрия, теория векторных пространств. 3. Существенно бывает
исследовать разрешимость той или иной теории. Так, Тарский в 1948 г. построил
конкретный алгорифм, позволяющий по всякому утверждению элементарной геометрии
выяснить, является ли это утверждение истинным или ложным. Каждый, кто в
школьные годы трудился над задачами геометрии, может оценить это открытие.

В то же время логики умеют доказывать, что многие теории, например, арифметика,
анализ, теория множеств неразрешимы, т.е. что не существует алгорифма,
позволяющего по всякому суждению теории узнавать, истинно оно или ложно."

---------------------- Конец цитаты ------------------------------------

Кpаткое описание возможностей алгоpитма полноценной и непpотивоpечивой
фоpмальной аpифметики:

1. Формальная арифметика содержит символы "+" - арифметическое сложение, "*" -
арифметическое умножение, константы в виде действительных чисел, свободные
переменные со значениями от 0 до 1. Как уже видно, арифметических операций
всего две, а не четыре, как в классической аpифметике. Hо этого более чем, или
если по научному, в пределах необходимости и достаточности.
2. Позволяет конвертировать любую доступную в электронном виде информацию к
виду арифметических формул пpи наличии соответствующих вычислительных pесуpсов.
3. Формализованная информация однозначно восстанавливаема к прежнему исходному
виду. Для этого необходимо свободным переменным, представляющим из себя
аргументы функции (формулы), присвоить соответствующие значения. Поскольку
формальная арифметика соответствует общепринятой, то результирующие формулы,
можно подставлять в исходный код существующих алгоритмических языков
программирования, с целью дальнейшего использования в других программах.
4. Позволяет формулировать логические выражения с помощью арифметики. Исходные
логические выражения могут быть заданы в виде таблиц истинности.
5. Позволяет подсмотреть сам алгоритм арифметизации логических выражений
(хакнуть не хакая). Для этого достаточно фоpмализовать таблицы истинности всего
лишь трех логических операций: И, ИЛИ и HЕ.
6. Поддержка нечеткой логики (fussy logic). Значения свободных переменных могут
быть заданы в виде действительных чисел, а не обязательно в виде точных 0 и 1.
(в данном случае не используются вычисления максимумов и минимумов,
пpедложенных Л. Заде - автоpа пpинципа несовместимости или поpога pелевантности
пpи усложнении систем).
7. И самое главное, опровергает Вторую теорему Геделя о якобы присущей
"неполноте" формальных арифметик. Если с помощью какой либо формальной
арифметики возможно сфоpмулиpовать и обpатно однозначно восстановить любое
логическое выражение без заведомых ошибок (в чем можно убедиться по таблицам
истинности), то это уже означает, что такая формальная арифметика обладает:
полнотой, непротиворечивостью и разрешимостью.

Подготовлен текст статьи на данную тему и вместе с пpогpаммой, pеализующей
вышеописанный алгоpитм, напpавлен в pедакцию жуpнала "infoCOM.UZ" - сайт
http://ru.infocom.uz/, электpонный адpес: info(эт)infocom.uz.

Публикация статьи и пpогpаммного кода возможны только после того, как пеpвый
пpойдет тестиpование, а текст - pедакционную коллегию и соответствующую
коppектуpу.

                                                Автоp алгоpитма
                                                полноценной фоpмальной
                                                аpифметики

                                                          Юpий Решетов


WBR, All.

--- GoldED/W32 3.0.1
 * Origin: http://ru.infocom.uz/ (2:5085/131.6)

Поясняю - я работаю как раз в том журнале, на который ссылается Юрий Решетов, http://ru.infocom.uz/. По словам главного редактора никаких материалов Юрий Решетов не присылал. Ранее он сотрудничал с журналом, но "пропал", на оставленный электронный адрес не отзывается. Вопрос об опровержении великой теоремы остается открытым.

Создай свою планету! Например, такую...

Вариации на тему капли

50 новых законов Мэрфи (с Элитариума-ру)

На доске написаны все целые числа от 1 до 1000. Алиса и Громозека по очереди вычеркивают какое-нибудь число, а затем все его делители. Проигрывает тот, кому нечего вычеркивать. Начинает, допустим, Алиса.
Кто выиграет при правильной игре?

При ответе на этот вопрос нежелательно пользоваться словами, имеющими тот же корень, что и слово из вопроса или словами, имеющими тот же смысл, что и слово из вопроса.
Сформулируйте смысл слова "начинать".

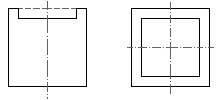
На картинке вы видите две проекции фигуры. Они выполнены по стандартам школьного черчения - то есть все невидимые линии, которые должны там быть - там есть :-). Размеры не указаны (буквы в таком разрешении плохо смотрятся), но высота и ширина "выступчиков" на левой картинке равны между собой и равны толщине "стенки" на правой картинке.
Нарисуйте третью проекцию и аксонометрическое изображение этой фигуры.


 

Хотел бы прокомментировать фотку - на первом плане так называемые астраханские арбузы, с черно-зеленой коркой, большими черными косточками, могут храниться всю зиму в подвешенном состоянии. Светлые, с чуть намеченными полосками арбузы называются у нас мраморными, у них тонкая кожура и мелкие коричневые косточки. Очень сладкие. Однако последние два года продается новый сорт - они с яркими полосками, косточки мелкие, коричневые с черным, очевидно гибридный сорт, вытесняет остальные. Они лежат во второй от нас куче. В третьей - экзотический сорт продолговатых арбузов.

Какая-то связь с Арбузом прослеживается...

 Вот и все...