Моделируя жизнь
Автор Андрей Тепляков.
Статья опубликована в №7 2001 Hard'n'Soft и доступна
на сайте журнала.
На Арбузе выложена для "концентрации"
занимательных сведений о числе пи.
Официальной датой рождения
метода Монте-Карло принято считать 1949 год, когда
в журнале Journal of American Statistical Association была
опубликована соответствующая статья С. Улама и Н.
Метрополиса. Впрочем, сам термин появился еще во
время Второй мировой войны, когда Джон фон Нейман
и Станислав Марцин Улам работали в Лос-Аламосе
над моделированием нейтронной диффузии в
расщепляемом материале. Что же это за метод и
почему он вызвал такой ажиотаж?
Определение метода (вернее, группы методов)
заложено в его названии: Монте-Карло — столица
европейского игорного бизнеса, где люди годами
ищут способы улучшить свои шансы в азартных
играх. Метод Монте-Карло — это метод решения
различных задач с помощью генерации случайных
последовательностей. Приемы метода Монте-Карло
были известны и до 40-х годов, но не получили
широкого распространения из-за больших объемов
вычислений. Появление ЭВМ сделало их практически
применимыми. Произошло это во многом благодаря
Джону фон Нейману, указавшему на ряд
перспективных задач, в которых целесообразно
применять методы имитационного моделирования,
например предсказание погоды, анализ запасов
нефти и гидродинамические расчеты.
Специалисты различают понятия имитационного и
численного моделирования: в первом случае
моделируется поведение всех компонентов
системы, во втором — только наиболее
существенных. Метод Монте-Карло относится к
имитационному моделированию, в котором при
расчете какой-либо системы воспроизводится и
исследуется поведение всех ее компонентов. Как
же можно моделировать сложную систему, не зная
строгих математических законов, которым она
подчиняется? Ответ на этот вопрос содержится в
назывании категории метода — «имитационный».
Если поведение системы достаточно сложно и нет
возможности описать его строгими
математическими формулами, необходимо поставить
определенное число экспериментов (т.н. случайных
испытаний) с каждым из узлов этой системы для
того, чтобы оценить, как они себя ведут.
После определенного числа случайных испытаний
мы получаем случайный вектор, в котором
содержатся значения отклика узла системы на
каждое испытание. Очевидно, что элементы этого
вектора имеют некоторое распределение,
описывающее поведение данного узла.
Немного отвлечемся и напомним, что такое
распределение. Распределением называется
совокупность значений, которые может принимать
случайная величина, и вероятностей, с которыми
она их принимает. Приведу два примера. Если вы
сейчас посмотрите на секундную стрелку своих
часов, то с вероятностью 1/60 увидите, что она
находится на некотором делении циферблата, т.е.
«попадание» любого из значений равновероятно.
Предположим, мы посмотрели на часы 95529 раз (это
значение выбрано случайным образом, как
иллюстрация того факта, что законы теории
вероятности проглядывают сквозь жизнь, где
крайне редко встречаются круглые числа),
записывая при этом число, которое мы видим.
Подсчитаем количество появлений значений и
построим соответствующую гистограмму.
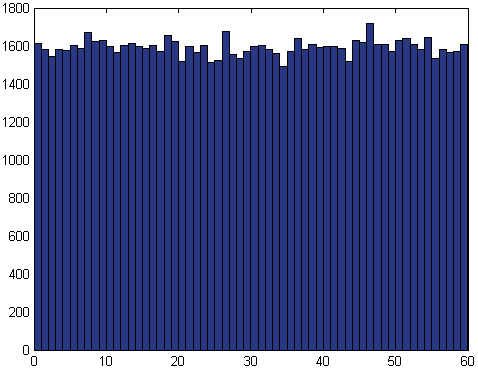
На графике по оси абсцисс
отложены показания секундной стрелки, а по оси
ординат — количество появлений данного числа.
Как уже упоминалось, вероятность появление
любого значения равна 1/60. Обозначим ее как p1:
p1 = 1/60 = 0,0167
Из гистограммы видно, что среднее число
появлений любого значения равно 1600. Обозначим
вероятность, полученную в ходе этого
эксперимента, как p2:
p2 = 1600/95529 = 0,0167
Итак, вероятности совпали. Рассмотрим второй
пример — машину, называемую «доска Гамильтона».
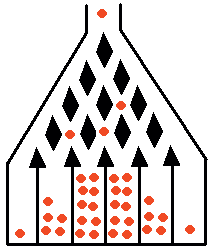
Принцип работы этого
устройства таков: металлические шарики
поступают в самый верхний канал. Наткнувшись на
первое острие, они «выбирают» путь направо или
налево. Затем происходит второй такой выбор и т.д.
При хорошей подгонке деталей выбор оказывается
случайным. Как видно, попадание шариков в нижние
лунки не равновероятно. В этом случае мы имеем
дело с гауссовым, или нормальным, распределением.
Чтобы моделировать какой-либо процесс,
необходимо знать, какому распределению он
подчиняется. Далее следует составить
математическую модель процесса. Но прежде чем
приступить к моделированию, еще немного истории.
Не секрет, что вероятность
появления орла или решки при подбрасывании
монеты равна 0,5. Определить ее экспериментально
пытались различные исследователи. Не имея в
своем распоряжении вычислительной техники, они
ставили эксперимент «в лоб», много раз
подбрасывая монету. Результаты экспериментов
приведены в таблице.
Результаты
эксперимента по подбрасыванию монеты |
Исследователь |
Число
подбрасываний |
Вероятность |
Жорж Бюффон |
4040 |
0,507 |
Огастес де Морган |
4092 |
0,5005 |
Уильям Джевонс |
20480 |
0,5068 |
Вс. Романовский |
80640 |
0,4923 |
Карл Пирсон |
24000 |
0,5005 |
Уильям Феллер |
10000 |
0,4979 |
В XVIII веке граф Жорж Луи Леклерк де Бюффон
сформулировал задачу о нахождении вероятности
того, что брошенная на разграфленный лист бумаги
игла пересечет одну из линий. Оказалось, что эта
вероятность связана с числом p, что сделало
возможным поиск этого числа вероятностными
методами, т.е. методом Монте-Карло! Эта задача
захватила умы многих исследователей. И сейчас,
уважительно называемая теоремой, она имеет ряд
интересных приложений. Попытаемся и мы посчитать
число p, имея в своем распоряжении такой мощный
инструмент, как компьютер.
На листе бумаги начерчены параллельные прямые,
находящиеся друг от друга на расстоянии L. На лист
брошена игла той же длины. Какова вероятность
того, что игла пересечет одну из прямых?
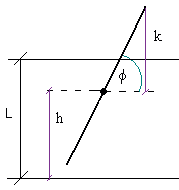 Положение иглы на листе
полностью определяется двумя независимыми
случайными величинами: углом ? (0 <? < ?) и
высотой h центра иглы (0 < h < L). Таким образом,
чтобы смоделировать одно выпадание иглы, нам
необходимо «разыграть» величины? и h. С величиной
h все просто. Будем считать, что центр иглы с
одинаковой вероятностью может оказаться на всем
отрезке [0,L]. Таким образом, получим h=rnd*L, где rnd —
случайная величина, имеющая равномерное
распределение. Теперь займемся поиском угла? , но
будем моделировать не сам угол, а значение его
синуса: 0 <sin ? <1. Чтобы моделировать синус
равномерно распределенного угла ?, нам
необходимо подобрать для него функцию
распределения, а это можно сделать на основе
эксперимента. Представим, что мы 10000 раз бросим
иглу, и каждый раз будем записывать значение sin ?
Подсчитаем число испытаний, в которых получено
каждое значение. Имея компьютер, нам
необязательно заниматься бросанием иглы на
самом деле, достаточно написать следующую
программу на Фортране: Положение иглы на листе
полностью определяется двумя независимыми
случайными величинами: углом ? (0 <? < ?) и
высотой h центра иглы (0 < h < L). Таким образом,
чтобы смоделировать одно выпадание иглы, нам
необходимо «разыграть» величины? и h. С величиной
h все просто. Будем считать, что центр иглы с
одинаковой вероятностью может оказаться на всем
отрезке [0,L]. Таким образом, получим h=rnd*L, где rnd —
случайная величина, имеющая равномерное
распределение. Теперь займемся поиском угла? , но
будем моделировать не сам угол, а значение его
синуса: 0 <sin ? <1. Чтобы моделировать синус
равномерно распределенного угла ?, нам
необходимо подобрать для него функцию
распределения, а это можно сделать на основе
эксперимента. Представим, что мы 10000 раз бросим
иглу, и каждый раз будем записывать значение sin ?
Подсчитаем число испытаний, в которых получено
каждое значение. Имея компьютер, нам
необязательно заниматься бросанием иглы на
самом деле, достаточно написать следующую
программу на Фортране:
do i=1,10000
rnd(i)=sind(180*rand())
enddo
С ее помощью мы получили интересующий нас
случайный вектор. Построим распределение его
составляющих.
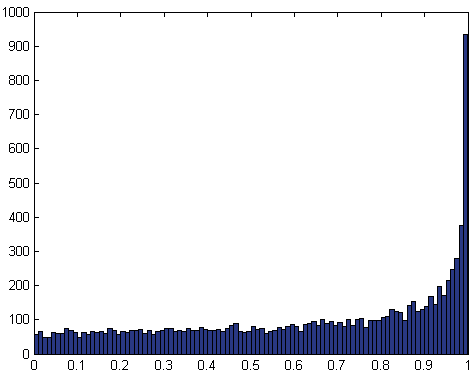
Мы видим перед собой некоторую
«помесь» равномерного и экспоненциального
распределений. Попробуем смоделировать то же
распределение, не бросая иглу и соответственно
не вычисляя напрямую значения синуса.
Воспользуемся программой, результат работы
которой представлен на рисунке
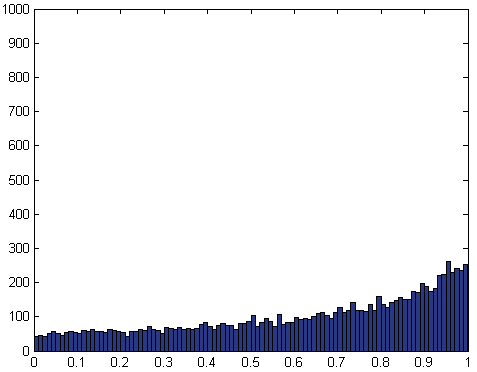
do i=1,10000
sinf=abs((rnd*exp(rnd**1.051))/ exp(1.)-1)
enddo
Визуально оба распределения похожи. Будем
считать, что распределение для sin f мы подобрали.
Теперь необходимо решить, как нам определять,
произошло ли пересечение или нет. По схеме (см.
выше) мы можем определить расстояние k (длина иглы
принимается равной L/2):
k = L sin f / 2
Очевидно, что при выполнении условий (L-h) < k (для
верхней линии) и h < k (для нижней линии) игла
пересечет одну из прямых. Для моделирования все
готово, и мы можем рассчитать методом Монте-Карло
вероятность p того, что игла пересечет линию.
Вместе с тем известно, что эта вероятность
выражается следующим соотношением
(доказательство этого факта в рамках данной
статьи я приводить не буду, желающие всегда могут
обратиться за дополнительной информацией к
математическим справочникам):
p = 2 / пи
Откуда
пи = 2 / p Теперь у нас все готово для расчетов.
Воспользуемся для этого программой на Фортране.
real(8) sinf,L,pi,k,x,x1,p,j,h,rnd
integer i,n
write(*,*) «Input L»
read(*,*) L
write(*,*) «Input n»
read(*,*) n
j=1
do i=1,n
rnd=fiboa()
sinf=abs((rnd*exp(rnd**1.051))
/exp(1.)-1)
k=(L/2)*sinf
h= rand()*L
x=L-h
x1=h
if(x.LE.k.OR.x1.LE.k) then
j=j+1
endif
p=j/i
pi=2/p
enddo
write(*,*) pi
end
Результаты нашего моделирования приведены в
таблице.
Вычисление числа
пи методом Монте-Карло |
| Число испытаний |
Генератор rand() |
| 1000 |
3,1104 |
| 10000 |
3,1363 |
| 100000 |
3,1523 |
| 1000000 |
3,1439 |
Рассмотренная задача
Бюффона — одно из очень многих приложений метода
Монте-Карло. С помощью этого метода
рассчитываются ядерные реакторы, он широко
используется в геофизике, экономике, биологии,
экологии и т.д., словом, для решения тех задач, где
аналитические или численные методы решения не
работают из-за высокой степени сложности.
Моделирование методом Монте-Карло — задача
увлекательная и вызывающая даже некоторый
трепет — еще бы, ведь моделируется сама жизнь! |



 Положение иглы на листе
полностью определяется двумя независимыми
случайными величинами: углом ? (0 <? < ?) и
высотой h центра иглы (0 < h < L). Таким образом,
чтобы смоделировать одно выпадание иглы, нам
необходимо «разыграть» величины? и h. С величиной
h все просто. Будем считать, что центр иглы с
одинаковой вероятностью может оказаться на всем
отрезке [0,L]. Таким образом, получим h=rnd*L, где rnd —
случайная величина, имеющая равномерное
распределение. Теперь займемся поиском угла? , но
будем моделировать не сам угол, а значение его
синуса: 0 <sin ? <1. Чтобы моделировать синус
равномерно распределенного угла ?, нам
необходимо подобрать для него функцию
распределения, а это можно сделать на основе
эксперимента. Представим, что мы 10000 раз бросим
иглу, и каждый раз будем записывать значение sin ?
Подсчитаем число испытаний, в которых получено
каждое значение. Имея компьютер, нам
необязательно заниматься бросанием иглы на
самом деле, достаточно написать следующую
программу на Фортране:
Положение иглы на листе
полностью определяется двумя независимыми
случайными величинами: углом ? (0 <? < ?) и
высотой h центра иглы (0 < h < L). Таким образом,
чтобы смоделировать одно выпадание иглы, нам
необходимо «разыграть» величины? и h. С величиной
h все просто. Будем считать, что центр иглы с
одинаковой вероятностью может оказаться на всем
отрезке [0,L]. Таким образом, получим h=rnd*L, где rnd —
случайная величина, имеющая равномерное
распределение. Теперь займемся поиском угла? , но
будем моделировать не сам угол, а значение его
синуса: 0 <sin ? <1. Чтобы моделировать синус
равномерно распределенного угла ?, нам
необходимо подобрать для него функцию
распределения, а это можно сделать на основе
эксперимента. Представим, что мы 10000 раз бросим
иглу, и каждый раз будем записывать значение sin ?
Подсчитаем число испытаний, в которых получено
каждое значение. Имея компьютер, нам
необязательно заниматься бросанием иглы на
самом деле, достаточно написать следующую
программу на Фортране:
