Сотовая связь, легкие и ягодицы Опубликовано в журнале Hard'n'nSoft №9 2001 Стр. 87

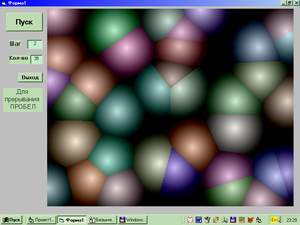
А пузырь - это, по-моему, очень интересно и изумительно
красиво. У Марка Твена есть такая восторженная
фраза: "Мыльный пузырь, пожалуй, самое восхитительное и самое
изысканное явление природы". Я не четко понимаю, что означают
слова "изысканное явление", но отчетливо вижу,
что Твен упивается созерцанием мыльного пузыря
Я.Е. Гегузин ПУЗЫРИ

Из многих замечательных и до конца не изученных свойств воды является, конечно же, эффект поверхностного натяжения. Благодаря ему струйка из крана утоньшается и разрывается, роса на траве в виде капелек, пылинки держатся на поверхности лужи, но, главное сегодня для нас - возможность поиграть с пеной и пузырями. Эти фантастические, если присмотреться, объекты красивы не только с эстетической точки зрения, но и тем, что тянут за собой шлейф занимательных задач. Прекрасная книжка о пузырях, процитированная в эпиграфе и выходившая когда-то в библиотечке «Квант», расположена на http://vivovoco.rsl.ru/VV/Q_PROJECT/BUBBLE/BUB_0.HTM

Как часто бывает, придумаешь алгоритм или увидишь картинку, и идея не отпускает, пока не сделаешь сам, не наиграешься с разными параметрами. Также и с пузырями. Суть в том, что задаются на плоскости случайным образом точки, и из них, как из центров, строятся окружности с увеличивающимися радиусами и уменьшающейся яркостью. А в каждой точке плоскости цвет берется от окружности с большей яркостью, то есть, ближайшей. Картинка похожа на взбитую пену. Программа не сложная (после многочасовой отладки - конечно…). Задается количество «пузырей», выбираются случайным образом их координаты, потом в цикле проходятся все точки плоскости с определением расстояния до ближайшего центра, и соответственно этому расстоянию уменьшается яркость. Небольшое замечание - экран надо перевести в режим 24-битного цвета, у меня было настроено на 16 бит и давало видимые перепады цвета. При 24 битах все гладко, даже при сохранении полученной картинки в формате JPG. Конечно, нетерпеливому читателю наплевать на описание программы - где обещанные ягодицы? Дело в том, что во время отладки на мой экран заглянул сослуживец (прапорщик) и воскликнул (пардон): «Да это же задница!!! Но чтоб с тремя-четырьмя ягодицами - такой я еще не видел…»

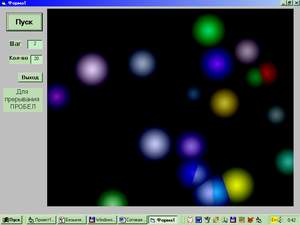
Увеличив количество пузырей до 100 или 200 получим пену, похожую на легкие, или какие-то другие внутренние органы, но явно биологического происхождения.

Увеличивая количество пузырей, мы заставляем их тесниться и уплотняться, в связи с чем возникают интересные задачи. Сколько соседей в среднем у каждого пузыря и как это зависит от тесноты? Влияет ли на вид пены (на количество соседних пузырей) скорость уменьшения яркости с ростом радиуса? Не находятся ли здесь некоторые фрактальные закономерности, связанные с размерностью объектов, если да, то как определить фрактальную размерность пузырей? И еще - интересно, мыльная пена такая же, как от пива, или ее параметры зависят от коэффициента поверхностного натяжения? При чем здесь сотовая связь? Мобильный телефон с помощью компьютера определяет антенну, сигнал от которой самый сильный, то есть, обычно ближайшую. При перемещении мобильника его сопровождение передается от одной антенны к другой, самой сильной для данной точки. Лучшей иллюстрации для этого процесса, чем наша картинка с пузырями не найти. Приступим к делу. Приведенная программа создана в Visual Basic 6, хотя вы можете реализовать этот нехитрый алгоритм на любом доступном языке, я, например, первые пузыри рисовал на Visual FoxPro 6.0. Создадим форму с четырьмя элементами: кнопками Пуск и Выход и двумя окошками TextBox для ввода шага движения (переменная ss, начальное значение равно шести) и количества пузырей (переменная v, начальное значение равно десяти). Процедура для кнопки Выход состоит из единственной команды End.

(В html отступы пропали, надеюсь, это не страшно...)

Private Sub Комманда1_Click()
Dim vc(), yc(), r()
Cls
Randomize (Timer)
xmax = 650
ymax = 530
'v = 5 Количество пузырей, передается из формы
'ss=6 Шаг движения по x и y, передается из формы
ReDim xc(v), yc(v), r(v) For i = 1 To v
xc(i) = Rnd * xmax
yc(i) = Rnd * ymax
Next i
For x = 5 To xmax Step ss
For y = 5 To ymax Step ss
For q = 1 To v
r(q) = ((xc(q) - x) ^ 2 + (yc(q) - y) ^ 2) ^ 0.5
Next q
For k = 1 To v - 1
For j = 1 To v - 1
If r(j) > r(j + 1) Then uu = r(j)
r(j) = r(j + 1)
r(j + 1) = uu
End If
Next j, k
red = 255 - Int(r(1))
green = 255 - Int(r(1) * 1.3)
blue = 255 - Int(r(1) * 1.1)
If ss > 1 Then Line (x, y)-Step(ss, ss), Col, BF
If ss = 1 Then PSet (x, y), Col Next y
Next x
End Sub Private Sub Комманда2_Click()
End
End Sub

Программа, а точнее процедура реакции нажатии кнопки Пуск, запускающая процесс появления пены, проста и (каламбур) прозрачна. Количество пузырей, точнее размерность массивов (переменная v), в которых расположены координаты центров и радиуса передается из формы. Причем, массив сначала объявляется пустым, а позже задается его размерность оператором Redim. Цикл с переменной i задает центры пузырей случайным образом. Для того, чтобы при каждом запуске датчик случайных чисел давал разные значения, его привяжем к текущему времени оператором Randomize(timer). В цикле с переменной q вычисляем для каждой точки с координатами x и y по теореме Пифагора расстояние до каждого из центров пузырей r(q) чтобы выбрать наименьший из них. Выбор происходит в циклах с переменными k и j. Разберите, как они работают - получите удовольствие от приобщения к классике программирования - сортировке массива по возрастанию методом пузырьков. Это не каламбур, название метода не имеет отношения к теме статьи, просто с каждым проходом цикла меньшие числа «всплывают вверх». Вообще говоря, переменная uu и присвоение ее значению r(j+1) нужно только в случае сохранения всего массива для дальнейшей работы, нас же интересует только наименьшее значение r(1), поэтому цикл можно сократить на две строки, имеющие лишь, скажем так, методический смысл. Получив минимальный радиус для текущей точки, можно приступать к формированию цвета, это и есть изюминка всей затеи. Каждая составляющая rgb-функции цвета уменьшается пропорционально радиусу. Меняя коэффициенты и максимальное значение 255 на меньшее, можно получать различные оттенки пены и регулировать контрастность рисунка.

Программа предоставляет безграничный простор для экспериментов. Попробуйте сделать, чтобы яркость не уменьшалась с удалением от центра пузыря, а увеличивалась, и будете поражены получившейся картиной. Попробуйте при вычислении радиуса поменять показатель степени с 0.5 на 0.55 или 0.45 (для этого мы и не воспользовались функцией Sqr). Попробуйте вместо формулы r2=x2+y2 применить r2=x2-y2 чтобы получить нечто гиперболическое… О бесконечных играх с цветами, шагом и количеством пузырей можно и не говорить. Естественно, что с уменьшением шага рисования и с увеличением количества пузырей время рисования возрастает, так как в каждой точке рисунка проверяются расстояния до всех центров пузырей, а все попытки оптимизировать алгоритм только добавят тормозов.

После написания статьи я периодически возвращался «к пузырям» и однажды осенило: а что, если разукрасить пузыри каждый в свой цвет. Тут пришлось поработать - ведь надо не только задать массив цветов для каждого пузыря и заполнить его случайным образом, но еще и отследить соответствие каждой точки плоскости не только ближайшему центру, но и его цвету. А это непросто потому, что при выборе наименьшего радиуса его индекс в массиве теряется. Задача (попробуйте!), конечно, решаемая, наверняка вы найдете изящное решение (и не одно) и будете сторицей вознаграждены получившейся картиной. Экран заполняется разноцветными шариками, как в моделях сложных молекул, или одинокими фонариками в зависимости от ваших настроек. {

Самые въедливые читатели, возможно, обратят внимание на обстоятельство, подмеченное моими сослуживцами, любителями пены - здесь все не до конца честно, так как все сферы получаются одного радиуса. Длительные размышления на эту тему с наблюдением мыльной, а чаще пивной пены к истине не приблизили, родив две мысли. Первая - это не делает картинку менее привлекательной. Вторая - ничто не противоречит тому, чтобы все пузырьки в пене имели равные радиуса, пусть кто-нибудь докажет обратное. Еще приятная идея, оставленная на будущее - можно сделать аплетик: в месте, где мы щелкнем мышкой «всплывает» пузырь, расталкивая ранее созданные. А при щелчке правой кнопкой пузырь лопается и его место занимают соседи. А еще хорошо бы на каждом пузыре делать радужный отблеск…

Вот и все, как ни странно, нам удалось связать вместе пену, Visual Basic, мобильники и … другие интересные предметы. Отладка программы и попутные опыты доставят вам массу удовольствия. Созерцание пузырей рождает прекрасные мысли, недоступные в обыденной суете, может в этом и состоит их предназначение, поразмышляйте об этом на досуге. Пишите. Постскриптум. Идея не моя, я увидел это чудо (как я сам не додумался!!!) на страничке Дмитрия Ланина «Красивые картинки с математическим содержанием» http://users.omskreg.ru/~lanin. В ходе переписки Дмитрий сообщил, что страничку «забросил», занят другими проектами. Спасибо ему за идею.