Ностальгия по арифметике

Существует три типа людей: те, которые умеют считать и те, которые не умеют.

Если бы опыт хоть капельку применялся, его бы не передавали из поколения в поколение.

Первый год века пусть надуманный, но все же рубеж, лишний раз предлагающий оглянуться на недавнее время. Ефим Шифрин, отвечая на вопрос, почему перестали пародировать Ленина и Брежнева, ответил, что время прошло, и для нынешней молодежи это такие же отвлеченные знаки как Батый. Такими же «ископаемыми знаками» стали телевизор с водяной линзой, узкоколейный трамвай с тамбурами и деревянными сидениями, а также примус с керогазом. Никто из детей не поверит, что можно было удивляться переносным радиоприемникам (помните - трапециевидная закругленная Спидола?) и шариковым ручкам, а появившийся 408й Москвич казался революцией в автомобилестроении.

Однако, помня, что чем шире угол зрения, тем он тупее, начинаем его сужать. Год моего поступления в школу был последним годом формы, державшейся с гимназических времен - гимнастерка с медными пуговицами, широкий ремень с пряжкой, форменная фуражка - в общем, Кондуит и Швамбрания. Прописи были каллиграфическими - с завитушками, жирными и волосяными линиями - тоже доживали последние годы вместе с перьевыми ручками и чернильницами.

А еще (подбираемся к главному) у нас была арифметика. То есть задачи решались не составлением уравнения с неизвестными, а поэтапно, арифметическими методами, отвечая на свои же сформулированные вопросы. Решения задач были неочевидными, эвристическими, каждый раз надо было проявлять изобретательность. Последующее изучение алгебры начисто перечеркнуло «арифметическое» мышление, я вижу, что потерял его (поэтому и отец не мог мне помочь по арифметике - все время пытался решать составлением уравнения). Через пару лет после моих мучений и саму арифметику отменили, сразу с первого класса вводили «икс» и от него плясали. Теперь, спустя почти сорок лет, мне почему-то стало жалко арифметику (старый стал…, кстати - красивое написание букв тоже жалко - корявым почерком высокую мысль не напишешь), она была трогательно красивой, более индивидуальной, более человеческой. С иксом-игреком конечно быстрее, но, как-то сухо, без души. Как кубики бульонные - быстро-питательно, но домашний борщ вкуснее и милее.

Приглашаю совершить прогулку в прекрасную забытую страну Арифметику. Уверен, что многие даже знают, с чего мы начнем - с беседы бессмертных чеховских персонажей: отставного губернского секретаря Удодова, его сына Пети и горе-репетитора Егора Зиберова, ученика VII класса гимназии: Теперь по арифметике... Берите доску. Какая следующая задача? Петя плюет на доску и стирает рукавом. Учитель берет задачник и диктует: - “Купец купил 138 арш. черного и синего сукна за 540 руб. Спрашивается, сколько аршин купил он того и другого, если синее стоило 5 руб. за аршин, а черное 3 руб.?” Повторите задачу. Петя повторяет задачу и тотчас же, ни слова не говоря, начинает делить 540 на 138. - Для чего же вы это делите? Постойте! Впрочем, так... продолжайте. Остаток получается? Здесь не может быть остатка. Дайте-ка я разделю! Зиберов делит, получает 3 с остатком и быстро стирает. “Странно... - думает он, ероша волосы и краснея. - Как же она решается? Гм!.. Это задача на неопределенные уравнения, а вовсе не арифметическая...” Учитель глядит в ответы и видит 75 и 63. “Гм!.. странно... Сложить 5 и 3, а потом делить 540 на 8? Так, что ли? Нет, не то”. - Решайте же! - говорит он Пете. - Ну, чего думаешь? Задача-то ведь пустяковая! - говорит Удодов Пете. - Экий ты дурак, братец! Решите уж вы ему, Егор Алексеич. Егор Алексеич берет в руки грифель и начинает решать. Он заикается, краснеет, бледнеет. - Это задача, собственно говоря, алгебраическая, - говорит он. - Ее с иксом и игреком решить можно. Впрочем, можно и так решить. Я, вот, разделил... понимаете? Теперь, вот, надо вычесть... понимаете? Или, вот что... Решите мне эту задачу сами к завтраму... Подумайте... Петя ехидно улыбается. Удодов тоже улыбается. Оба они понимают замешательство учителя. Ученик VII класса еще пуще конфузится, встает и начинает ходить из угла в угол. - И без алгебры решить можно, - говорит Удодов, протягивая руку к счетам и вздыхая. - Вот извольте видеть... Он щелкает на счетах, и у него получается 75 и 63, что и нужно было. — Вот-с... по-нашему, по-неученому.

Конец цитаты. Кто-нибудь сможет решить без икса, на счетах? Ладно, счеты не найти, на калькуляторе? Печально. Рассмотрим, как же решал губернский секретарь и двести шестьдесят поколений гимназистов и октябрят - первый учебник «Арифметика Магницкого» вышел в 1703 году. Сначала узнаем, сколько заплатил бы купец, если бы купил все 138 аршин по 5 рублей: 138*5=690. На сколько это больше, чем он заплатил? 690-540=150. А так как каждый метр синего сукна на 5-3=2 рубля дороже черного, то, разделив 150 на эти 2 рубля, получим 75 метров черного сукна. И соответственно 63 метра синего. Красиво? Да. Очевидно? Нет, если не знать этот прием, можно долго делить 540 на 138…

Теперь, конечно, наши любимые полтора землекопа, бассейны с трубами или, машинистки, печатающие рукопись (ужас - без Word’a и даже без Лексикона!). Итак, более опытная машинистка могла бы перепечатать рукопись за два часа, менее опытная - за три часа. За сколько часов они перепечатают, работая вместе? Итак, время пошло - и печати рукописи и вашего решения без «икса». Один из вариантов решений выглядит так. За шесть часов первая напечатала бы три экземпляра рукописи, а вторая два, а вместе пять экземпляров. Значит, один экземпляр за 6/5 часа или 1 час 12 минут. Еще один, не менее красивый вариант решения. Первая машинистка работает в полтора раза быстрее второй, значит и ее доля работы будет в полтора раза больше, или, первая выполнит 3/5 а вторая 2/5 работы. Но известно, что всю работу первая делает за 2 часа, значит 3/5 работы она выполнит за 6/5 часа. И, конечно, самый классический вариант: принимаем всю работу за единицу, тогда скорость первой будет 1/2, скорость второй 1/3, суммарная скорость 1/2+1/3=5/6. Делим работу на скорость, получаем те же 6/5. Вот так - мы уже три раза решили, а они еще печатают…

Главное при занятии любимым предметом - не переборщить. Напоследок предлагаю читателям проверить, место ли им в третьем классе дореволюционной гимназии с помощью заковыристой задачи. Два парома отчаливают одновременно и встречаются на расстоянии 720 метров от берега. Прибыв к месту назначения каждый паром стоит 10 минут и отправляется обратно. Паромы вновь встречаются в 400 метрах от другого берега. Чему равна ширина реки?

Тот же самый Ефим Шифрин, цитируемый в начале статьи, на вопрос, почему его отец не одобрил выбор профессии артиста произнес страшные слова. Отец, проведший много лет на каторге, сказал, что надо выбирать специальность, которая может пригодиться в лагере. То есть, рано списывать недавнюю историю в архив, пока живы ее свидетели и участники. (Потом - ладно.) В том числе и арифметику.

Опубликовано в Компьютерре №409

О задаче про паромы (решение по многочисленным просьбам)

В статье «Ностальгия по арифметике» (В Компьютерре №409) я предложил решить задачу о паромах: «Два парома отчаливают одновременно и встречаются на расстоянии 720 ярдов от берега. Прибыв к месту назначения каждый паром стоит 10 минут и отправляется обратно. Паромы вновь встречаются в 400 ярдах от другого берега. Чему равна ширина реки?». После этого получил много писем, одни авторы доказывали невозможность решения, другие описывали свои безуспешные попытки составить системы уравнений, и все просили решения задачи. Самое печальное, что я сам ее решить не смог. Задача эта принадлежит известному выдумщику Сэму Ллойду (Математическая мозаика. М., Мир, 1980, задача №131), но решение он приводит запутанное и непонятное. Эта же задача есть и у Генри Эрнеста Дьюдени (Кентерберийские головоломки. М., Мир, 1979, задача №99), не менее известного автора головоломок, правда у него фигурируют посыльные от мясника к пекарю и от пекаря к мяснику. В решениях Дьюдени пишет лишь, что надо сложить сумму расстояний из задачи с удвоенной их разностью, то есть 720+2*(720-400)=1760 ярдов или одна миля без объяснений. И только у Мартина Гарднера, мэтра популярной математики, включившего эту задачу в свою книгу (Математические головоломки и развлечения, М., Мир, 1971, страница 99, эта книга первая в замечательной серии) мы найдем толковое изящное решение задачи.

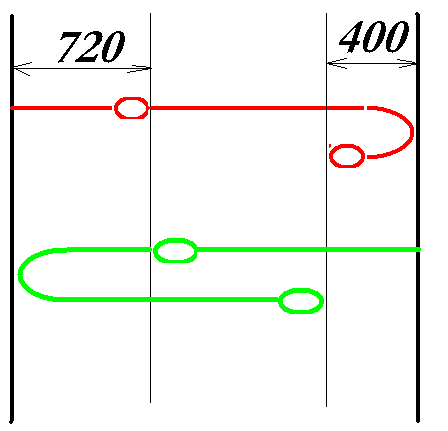
Когда паромы встречаются первый раз, сумма пройденных ими расстояний равна ширине реки. Когда каждый из них причаливает к противоположному берегу, эта сумма равна удвоенной ширине реки, а когда они встречаются второй раз, сумма пройденных ими расстояний в три раза больше ширины реки. Поскольку оба парома двигаются с постоянной скоростью в течение одного и того же промежутка времени, мы можем заключить, что к моменту второй встречи каждый из них прошел расстояние втрое больше пройденного к моменту первой встречи. Поскольку красный паром прошел до первой встречи 720 ярдов, к моменту второй встречи все пройденное им расстояние равно 720*3=2160 ярдов. Из схемы видно, что это на 400 ярдов больше ширины реки, поэтому из 2160 надо вычесть 400, получится 1760 ярдов. Это и есть ширина реки. Время стоянки в решение не входит. К решению задачи можно подойти и иначе. Пусть ширина реки х. Вначале отношение расстояний, пройденных паромами, равно (х-720)/720. Ко второй встрече оно будет составлять (2х-400)/(х+400). Эти отношения равны, из них легко находится х.

Вариант решения от Скляревского Павла:

Второй паром (красный на схеме) до первой встречи прошел х-720 ярдов, а до второй - втрое больше. Но ему не хватило 400 ярдов до берега. Поэтому можно приравнять 3*(х-720) и 2*х-400. Отсюда х=1760

Не правда ли красиво и невероятно просто?