«Жизнь» сложить – не поле перейти…

(Опубликовано в Домашнем компьютере №2/2002)

В соавторстве с Константином Кнопом, konstantin@knop.com

Рост числа нежеланных потомков создает адское положение
 как для семьи, так и для разрушителей семейных традиций. 
Предки таких семей падают вниз, так как приношение им воды и 
пищи полностью прекращается.
Бхагавад-гита. На поле битвы Курушкетра. Текст 41.

Что из новостей на стыке науки и программирования запомнилось ярче всего? Многие согласятся, если мы ответим – генетические алгоритмы (ГА), моделируемые на компьютере. «Компьютерра» сообщала, например, о работах, когда создавалась колония программ, решающих так называемую задачу коммивояжера (поиска оптимального маршрута между несколькими городами), потом из программ отбирались самые успешно справляющиеся с задачей, программы скрещивались случайным образом, обмениваясь фрагментами кода, снова отбирались и скрещивались…  В результате оставались жить несколько самых успешно работающих программ. Именно несколько, приблизительно одного уровня, а вовсе не один «супергений».
Еще было подмечено, что очень часто потомки «успешных» программ работают хуже своих родителей. Это напомнило сетования знакомых на то, что дети не умнее своих родителей. Да и так все видят, что со времен Архимеда и Пифагора человечество в лучшем случае не поумнело. В общем, вся надежда на генетические алгоритмы.
Вспоминается бородатая шутка о том, что сумма разума величина постоянная, а население Земли постоянно растет… Впрочем, эти маловразумительные доводы меркнут перед тем фактом, что заниматься любыми моделями, живущими программной жизнью, необычайно интересно. Вряд ли вы найдете более приятный вариант общения с компьютером. Опять же пусть маленький, но вклад в процесс создания пресловутого искусственного интеллекта. Заинтересовавшимся моделистам рекомендую статью «Популярно о генетических алгоритмах». Перекликается с темой и статья «Наследственность у биоморфов» 

Предлагаю вместе пройти несколько шагов, обратившись к игре «Жизнь». «Компьютерра» писала о ней очень давно, в №243. Статья содержит много полезных ссылок, но за прошедшие четыре года появились интересные русскоязычные ресурсы, в первую очередь это клуб «жизнелюбов»  и страничка программы Fam  с хорошей подборкой ссылок.
Еще одно замечание. Впервые рассказ об этой игре появился в книге Мартина Гарднера «Математические досуги» (М., Мир, 1972), а не в его же книге «Крестики-нолики» (М., Мир, 1988), как указано в процитированных выше источниках. Разница в 16 лет между выходами этих книг, несущественная ныне, для авторов была очень важна – прочитав еще школьниками первую книгу, они увлеклись задачей исследования «Жизни». Позже мы частенько возвращались к этой забаве, с удовольствием встречая редкие статьи о ней в «Кванте» или «Науке и жизни». Вторую же книгу мы читали, уже имея регулярный доступ к компьютерам. Так что она была для нас уже не теоретическим учебником, а практическим руководством…

Все вышесказанное было вступлением, больше не отвлекаемся, переходим к делу.
Традиционная «Жизнь», правила которой были разработаны Дж.Конуэем после многочисленных экспериментов, покоится на трех китах:
1) каждая особь, у которой есть 2 или 3 соседние особи, выживает – то есть переходит в следующее поколение; все остальные особи погибают.
2) в каждой пустой клетке, у которой есть рядом 3 живые соседние клетки, в следующем поколении рождается новая особь.
Cмена поколений происходит тактами, за один такт генетические законы применяются одновременно ко всем клеткам доски. Соседними в "Жизни" считаются клетки, примыкающие друг к другу либо сторонами, либо углами
Итак, имеется «коэффициент рождаемости», равный 3, и «диапазон выживания» от 2 до 3 (клетки с меньшим числом соседей гибнут «от одиночества», а клетки с большим числом соседей умирают от «перенаселения»). Именно такие числа гарантируют для клетчатой «Жизни» наиболее интересное поведение. За сорок лет существования этой игры этому поведению посвящены уже тысячи статей в разнообразных научных и научно-популярных журналах. За последние двадцать лет созданы десятки программ, моделирующих «Жизнь», в том числе и разнообразные хранители экрана для Windows. По-видимому, наилучшая коллекция ссылок содержится в Yahoo http://dir.yahoo.com/Science/Artificial_Life/Cellular_Automata/Conway_s_Game_of_Life

Один из авторов этой статьи пошел немного в другом направлении и сам запрограммировал «Жизнь» на доске с шестиугольными ячейками. Во-первых, известно, что перенос с прямоугольной на шестиугольную доски добавляет интересные особенности в привычные игры. Известны несколько вариантов гексагональных шахмат  и шестиугольный вариант игры «Волк и семеро козлят». Другие забавные игры на таком поле можно найти здесь.
Во-вторых, шестиугольное поле ближе к природным образованиям (те же соты), чем прямоугольные доски. Наконец, в-третьих – автору было просто интересно. Далее уже дело техники, форма, код, отладка, и повозившись вечерок, получили симпатичную программку.

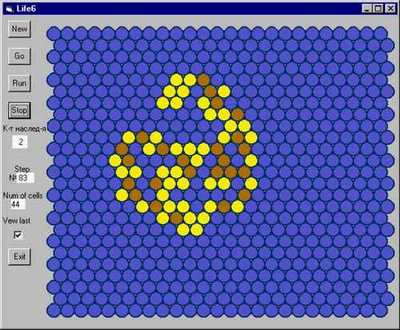
Причем все изображенные здесь «фичи» – вывод предыдущего поколения, кнопки работы пошагово или автоматом, задание конфигурации мышкой или случайным образом и прочие удобства – не более, чем обрамление основной идеи. А она заключена в выборе законов нашей шестиугольной жизни. (Появляются иногда удивительные «мигалки», «вертушки» и прочие чудеса – но не будем отвлекаться.)
Если живая ячейка переходит в следующее поколение в случае трех живых соседей, то процесс протекает интересно, но недолго. Если выживание происходят при двух и, тем более при одном соседе, организм неограниченно растет. Если назначить «порог выживания», равный четырем, то организм быстро погибает.
Так же и с появлением новой жизни – при двух соседях колония устойчива, при одном – взрывообразно растет, при трех и более – быстро погибает.
Итак, внимание, основная изюминка, из-за которой и городился огород. В идеале хотелось бы иметь такое количество соседей, чтобы развитие колонии «Жизни» было столь же непредсказуемым, как в классическом варианте. Очень хочется иметь дробное число соседей – между двумя и тремя! Но дробные числа тут, естественно, недопустимы. Однако ничто не мешает выбирать эти числа случайным образом в определенном диапазоне для каждого шага, введя поправочный коэффициент. А этот коэффициент, в свою очередь, делаем зависимым от количества активных ячеек в колонии. И получаем эффект автоматического регулирования численности стада (или стаи), которое колышется на экране, то уменьшаясь, то разрастаясь. Колония проживает 600 и даже более смен поколений, пока, несмотря на оптимизацию, натыкается на совсем плохую конфигурацию и погибает.
Присоединяйтесь! Не к ним, конечно, а к нашим исследованиям. Это действительно увлекает. Кому лень кодировать – здесь можно скачать готовую программку. (ZIP-архив формы, кода и выполняемого exe-файла всего 10 кб)
Другую (онлайновую, точнее, Java-аплетную) реализацию игры «Жизнь» на шестиугольной доске можно найти на здесь. Там можно выбрать один из шести вариантов «правил жизни». Первые пять описаны при помощи картинок: 
«Худой» вариант: рождение живой клетки в центре прямоугольника происходит только в том случае, если она сама или ее соседи на последнем такте имели следующее расположение: 

Разумеется, эти расположения приведены с точностью до поворотов и отражений. 
«Средний» вариант: в дополнение к «худому», приведены еще две картинки, при которых в центре шестиугольника на следующем такте появляется живая клетка. 

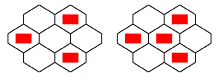
"Толстый» вариант: еще две картинки в дополнение к "среднему" 

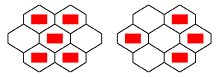
«Вариант Голея»: четыре порождающих картинки

«Вариант Престона» – основан на варианте Голея, добавлена еще одна картинка 

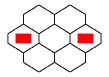
Шестой – «Вариант Каллахана» – показан на экране, но не описан. Можете рассматривать отыскание его правил как экспериментальную задачку, которую мы дарим вам напоследок!