Рогатая гусеница Опубликовано в журнале Hard'n'nSoft №9 2001 Стр. 85

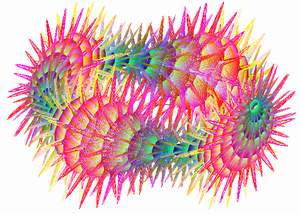
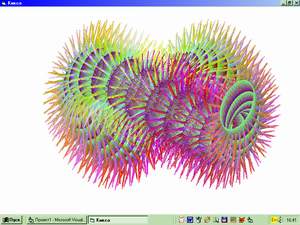
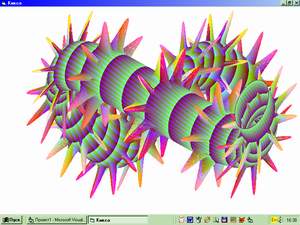
Алиса и Синяя Гусеница долго смотрели друг на
друга,не говоря ни слова. Наконец, Гусеница вынула
кальян изо рта и медленно, словно в полусне, заговорила:
– Ты… кто… такая? - спросила Синяя Гусеница.
Льюис Кэрролл. Приключения Алисы в Стране Чудес.

Великий сказочник сказал нам не всю правду. Гусеница была не столько синяя, сколько рогатая, так как курила всякую гадость. Причем рожек было много, в чем мы с вами вскоре и убедимся. Но прежде поговорим о торе. Тор - это тело, образованное вращением окружности вокруг оси, лежащей в плоскости этой окружности и не пересекающей ее. Самые понятные примеры - бублики и камеры от велосипедного колеса. С тором связано большое количество занимательных задач, желающим дам ссылочку. Добавим только пару высоконаучных соображений. Если бы Земля была не шаром, а тором, то при столкновением с огромным астероидом есть вероятность, что он пролетит в «дырку». И еще - селекционеры вывели торообразный арбуз, его удобно переносить, продев руку в отверстие. Нас же сейчас тор интересует как объект для рисования. Создадим форму в Visual Basic’e и напишем процедуру, связанную с открытием формы. Запустим два цикла: с переменной j (она же угловой параметр s для прорисовки малого круга с радиусом RR1) и переменной i (угловой параметр t для вращения малого круга в плоскости XZ радиусом RR. Проекцию оси Z направим под 60 градусов к оси X, для перевода объемной картинки в плоскость экрана используются переменные X1 и Y1. Если в приведенном тексте программы мы оставим RR0=RR1 и при вычислении z уберем множитель 2 при t, то у нас нарисуется самый обычный тор. Обратите внимание на расцветку, она задается переменными red, green и blue и полностью в вашей власти. В приведенном примере красный цвет пропорционален текущему радиусу малого круга и появляется только на «вздутиях» и на рожках, зеленый пропорционален i, что дает поперечные полосы, а синий зависит от произведения i*j и проявляется в виде голубых полосок.

(В html отступы пропали, надеюсь, это не страшно...)

Private Sub Form_Load()
xx = 430
yy = 260
P = 3.1415926
RR = 240
RR1 = 60
For i = 0 To 360 Step 0.5
For j = 0 To 360 Step 2
t = i * P / 180
s = j * P / 180
RR0 = RR1 + 60 * (Sin(2 * t)) ^ 2 X = RR * Cos(t) + RR0 * Cos(s)
Y = RR0 * Sin(s) z = RR * Sin(2 * t) + RR0 * Cos(s)
X1 = X - z * Cos(P / 3) * 0.5
Y1 = Y - z * Sin(P / 3) * 0.5
red = 255 * RR0 / (RR1 + 60)
green = 255 * i / 10 Mod 255
blue = 0.1 * i * j Mod 255
Line (X1 + xx, Y1 + yy)-(X2 + xx, Y2 + yy), RGB(red, green, blue)
X2 = X1
Y2 = Y1
Next j
Next i
End Sub

Насмотревшись на скромный и унылый тор начинаем над ним издеваться. Вернем двойку при t в синусе при вычислении z. Это перехлестнет тор и он будет выглядеть в форме восьмерки. Вернем «искажения» при вычислении RR0 и получим картинку, явно претендующую на то, чтобы Зигмунд Фрейд предлагал ее своим пациентам для диагностики отклонений.

Опыты со слагаемым RR1 наиболее эффектны - попробуйте поменять множитель при синусе (60), множитель при t и показатель степени, в которую возводится синус и будете вознаграждены появляющимися существами. Однако, подбираемся к главному - введите для RR0 выражение: RR0 = RR1 + 60 * Sin(2 * t) ^ 2 + 60 * (Sin(8 * s)) ^ 24 * Sin(16 * t) ^ 24 Первое слагаемое с RR1 дает уже рассмотренные нами утолщения, а вот второе слагаемое и дает рожки на торе, или, точнее, уже на гусенице. Причем множитель при s дает количество рожек на малом круге, множитель при t - на большом круге, показатели степени определяют плавность или крутизну рожек, а передний числовой множитель (60) - их высоту. (Если показатель степени будет нечетным, то отростки будут не только наружу, но и внутрь, порождая на экране мерзкие существа.) По правде говоря, тут наша виртуальная гусеница не столько с рожками, как было заявлено, сколько с колючками и четырежды «в положении», если такое возможно у гусениц. Но читатель теперь владеет волшебными знаниями для создания любых гусениц (не обязательно замкнутых) с любыми рожками-колючками-чешуей.

Конец.