Кони, трактор - оборот картинок

В каждой книжке по занимательной физике обязательно присутствует красивая задача: "Какая точка трамвая всегда движется в обратную сторону относительно движения самого трамвая?" Пока думайте и одновременно читайте дальше. Если монета катится по неподвижной монете такого же диаметра, то сколько раз она обернется вокруг своей оси за один оборот вокруг монеты? (Не спешите с ответом...) А если неподвижная монета в два раза больше? В два раза меньше? А вокруг двух прикасающихся монет? Не торопитесь, все не так просто. А если (а сколько задач одновременно вы можете решать, проверьте) вы обходите вокруг дерева, держась все время к нему лицом, вращаетесь ли вы вокруг своей оси? Вращается ли в это время стрелка вашего компаса относительно вашей руки? А если вы крадетесь за белкой, которая прячется от вас за деревом, вращаетесь ли вы относительно белки, если вы с ней все время повернуты друг к другу лицом? Совпадает ли угловая скорость вращения Луны вокруг Земли с угловой скоростью вращения Луны вокруг своей оси по направлению и величине? Почему брызги с заднего колеса велосипеда попадают на велосипедиста? Чем больше размышляешь о преимуществах колесного качения над ползанием и шаганием, тем больше удивляешься, что природа не использовала этот путь. Разве что ветер катит перекати-поле и почему-то говорят, что в голове шарики крутятся, когда мы думаем? Как у вас с этим делом? Что за фразы в названиях статьи и ее разделов, вы их узнали? Тогда вернемся к трамваю. В обратную сторону всегда движется точка на реборде колеса ниже рельса. Реборда - это фланец на колесе, не позволяющий съехать с рельса. 
Траектория, описываемая точкой катящегося колеса, называется циклоидой. Точка, лежащая на поверхности катящегося колеса будет "рисовать" арки с остановками в точках касания с рельсом. Точки, лежащие на колесе ближе к его центру будут "рисовать" более плавные арки, переходящие в прямую линию при приближении точки к центру колеса. Точки, лежащие дальше точки качения, например, на реборде, в зонах ниже рельса "нарисуют" обратные петли, в которых и происходит движение "назад".
Особый интерес представляют так называемые эпициклоиды и гипоциклоиды, описываемые токами колеса, катящегося по окружности снаружи или внутри ее соответственно. Когда-то продавалась игрушка "Спирограф", состоящая из набора зубчатых колесиков с отверстиями для карандаша. Закрепив одно колесо надо было обкатывать его другим, вставив карандаш или ручку в отверстие в подвижном колесе. При этом получались очень красивые узоры - цветы, бабочки, звезды и т. д. Все, что связано с циклоидами, имеет очень красивые проявления, что дало основание мэтру популярной математики Мартину Гарднеру назвать циклоиду "Прекрасной Еленой геометрии". Процесс этот, как вы уже, наверное, почувствовали, просится для программирования, обещая интересную забаву и красивые узоры. Тому, кто терпеть не может программирование и программистов, а циклоидами заинтересовался, рекомендую поиграть с Java-аплетом, скачанным со странички Ани Гарга из Индии www.wordsmith.org/~ani/java/spirograph.html  Спасибо автору аплета, я послал ему письмо с благодарностью.

Однако, мне кажется, что циклоиды здесь рисуются не совсем правильно.

Роз узор

Мы же, перефразируя французскую поговорку "Кто сам пилит свои дрова, согревается дважды", заметим, что "Кто сам программирует свои игрушки, наслаждается дважды!" Процесс программирования циклоид несложен и увлекателен, достаточно "пройтись" в цикле по формулам:

X = Int((R1 + R2) * Cos(R2 * T / R1) - R3 * Cos((R1 + R2) / R1 * T))
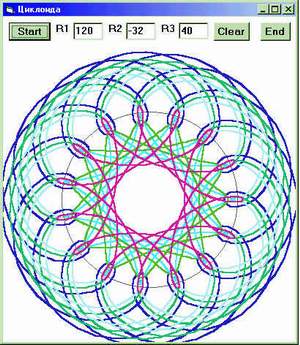
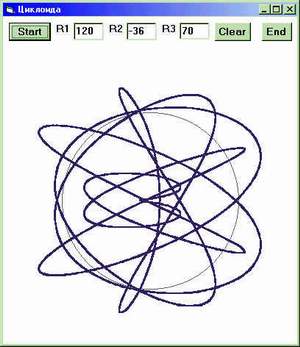
Y = Int((R1 + R2) * Sin(R2 * T / R1) - R3 * Sin((R1 + R2) / R1 * T))

Здесь R1 - радиус круга, по которому катится колесо, R2 - радиус колеса, катящегося по кругу, если с минусом, то внутри его и R3 - радиус, на котором лежит рисуемая точка на колесе. Т - счетчик цикла, он же полярный угол, на котором лежит центр колеса в данный момент. Создадим форму с вводом значений радиусов и кнопками управления (кому лень - пишите, вышлю) и можем наслаждаться игрушкой, оторваться от которой невозможно. При R3=R2 имеем частный случай точки на ободе колеса, при увеличении R3 (реборда) появляются петли, при уменьшении траектория сглаживается, вырождаясь в круг при R3=0. Первое удовольствие от игрушки - менять R3 и наблюдать сказочные узоры. Второй шаг - воспоминание об изучаемом в младших классах наименьшем общем кратном двух чисел. Если R2 равен трети R1, то нарисуется три лепестка, если четверти, то четыре, что не так интересно. Но если задать R1=120 и R2=32, то циклоида нарисует 15 лепестков, обойдя по кругу четыре раза. 

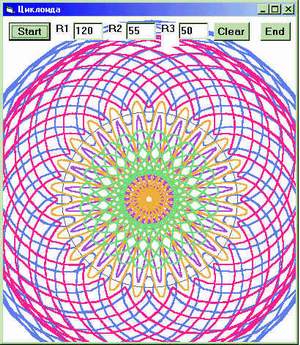
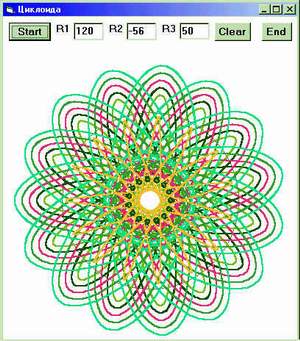
То есть, для нахождения наименьшего общего кратного (480) в разложении числа 120 на простые делители не хватает двух двоек, а у 32, соответственно, 3 и 5. Задание взаимно простых R1 и R2 (120 и 29) приведет к сплошному замазыванию траектории, так как лепестки никогда не наложатся повторно. Самые красивые картинки получаются при "слегка" некратных радиусах, например, 120 и 27, 120 и 35, 120 и 55, 120 и 56. Сразу же можно рисовать и с отрицательными значениями R2, проверяя те же закономерности внутри круга с разными значениями R3. 

А как изменится картинка, если поменять знак у R3? И еще вопрос (из книги "Россыпи головоломок" Стивена Барра, М.,Мир, 1987): точка на колесе с радиусом, в шесть раз меньшим, чем радиус круга, внутри которого оно катится, нарисует шесть арок. А что нарисует точка на колесе с радиусом, равным 5/6 радиуса круга? Подскажу - как ни странно, но на два последних вопроса ответ один и тот же.

 А что будет, если R1 задать отрицательным? А если одновременно с R2? Тем и хороша программная модель, что на ней можно наблюдать траектории, недостижимые на материальной игрушке. Привожу текст программы на VB6, вам надо только cоздать форму, назвать ее Циклоида и назначить размерность в пикселях. Также необходимо создать три скроллбара - ползунковых регуляторов для радиусов, переменные R11,R22 и R33.

Dim XX, YY, red, blue, green As Integer, T, DELTA As Single
Private Sub Clear_Click()
   Cls
   Циклоида.DrawWidth = 1
   Circle (XX, YY), Abs(R11), RGB(100, 100, 100)
End Sub
Private Sub End_Click()
   End
End Sub
Private Sub Form_Load()
   Randomize (Timer)
   XX = 200
   YY = 250
   T = 0
   DELTA = 0.25
   Циклоида.DrawWidth = 1
   Circle (XX, YY), R11, RGB(100, 100, 100)
End Sub
Private Sub Start_Click()
   red = Rnd * 255
   green = Rnd * 255
   blue = Rnd * 255
   R1 = Val(R11)
   R2 = Val(R22)
   R3 = Val(R33)
   Циклоида.DrawWidth = 2
   For T = 0 To 64 * 3.14159 Step DELTA
      X1 = Int((R1 + R2) * Cos(R2 * T / R1) - R3 * Cos((R1 + R2) / R1 * T))
      Y1 = Int((R1 + R2) * Sin(R2 * T / R1) - R3 * Sin((R1 + R2) / R1 * T))
      'R2 = -R2
      'R1 = -R1
      'R3 = -R3
      If T > 0 Then Line (X1 + XX, Y1 + YY)-(X2 + 200, Y2 + 250), RGB(red, green, blue)
      Refresh
      X2 = X1
      Y2 = Y1
   Next T
End Sub Private
Sub Form_KeyPress(keyascii As Integer)
If keyascii = 32 Then End
End Sub

Скачать исходники, форму и exe-шник.  ZIP-архив 6.981 байт

Осело колесо

Возьмем и поменяем знак у R3 внутри цикла, задав R3=-R3, и получим монстра:

Можно проделать такой трюк и с R2, тогда точки эпициклоиды будут соединяться с соответствующими точками гипоциклоиды, рисуя фантастических ежей. 
В статье "Прогулки по паутине" (КТ №397) я писал, что можно было бы вспомнить фигуры Лиссажу, но не стоит смешивать две забавы. На что получил письмо от автора "Речки" www.rechka.ru с вопросом - а почему бы собственно и не смешать? Причем автор именно "смешал" и получил невероятно красивые изображения и выложил их на "Речке". Так вот, можно применить фигуры Лиссажу и к нашим циклоидам, заставив, например, колесики катиться по восьмеркам-лепесткам-розеткам, или, наоборот, катить по колесу замысловатые фигуры. Катить же фигуры Лиссажу по фигурам Лиссажу - это, согласитесь, слишком забористо. Первая же картинка напомнила мне, что этой весной я просил Дмитрия Красновского, ведущего рубрики Изо Компьютерры-онлайн, написать статью-руководство по созданию красивых вензелей, например, для оформления поэтических страничек. Дмитрий просьбу выполнил, разместив в Изо руководство по созданию вензелей в Corel Draw. Дело за малым - как придумать красивый вензель? И тут уж наша игрушка вам выдаст массу образцов на выбор.

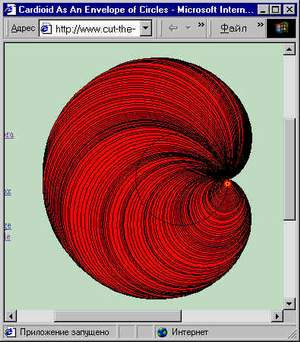
Кстати, создатель вышеупомянутой "Речки" выложил симпатичную программу, рисующие циклоиды, и картинки "лиссажушных" циклоид.

А знакомый по переписке YAR получил удивительные изображения розеток, которые можно использовать для исключения подделок банкнот и других бумаг. Увидеть эти красивые создания можно здесь.

А сыр катит и та крыса

Когда наиграетесь с экспериментами, программу можно модифицировать так, чтобы радиуса R1 и R2 выбирались случайным образом (из "хороших" диапазонов, разумеется), а R3 задавать несколько значений от нуля до ста (например) - получится неплохая заставка для отдыха. Напоследок, когда отдохнете, решите задачу, из коллекции Гарднера: девушка с круглой талией вращает обруч вдвое большего (чем талия) радиуса. Какое расстояние (в радиусах талии) пролетит точка, коснувшаяся пупка до следующего с ним соприкосновения? Траектория этой точки описывает линию, которая называется кардиоидой, так как она похожа на сердце. (Частный случай улитки Паскаля, кстати, тоже фигурировавший в статье "Прогулки по паутине".) Если у вас не закружилась голова от предлагаемой картины, то страничке профессора математики университета Айовы Александра Богомольного (http://www.cut-the-knot/pithagorfas/cycloids.html) вы сможете найти симпатичный аплет, рисующий кардиоиду.

Там же найдете элегантную идею расчета эпи- и гипоциклоид - действие происходит на плоскости комплексных чисел, что позволяет использовать формулу Муавра и представление комплексного числа в показательной форме по формуле Эйлера.
И, наконец, вернемся к задачах о монетах, которые добросовестные читатели решали во время чтения статьи. Первое пришедшее в голову решение, что монета, катясь по такой же монете при обходе поворачивается на один оборот, будет неверным! 

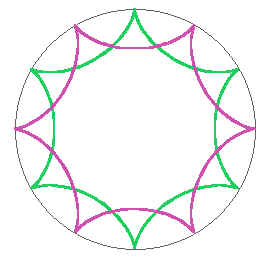
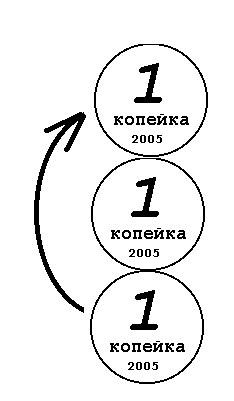
Посмотрите на картинку и проверьте лично: при обкатывании из нижнего положения в верхнее монета сделает (как ни странно) полный оборот, а, значит, при полном обкатывании - два оборота! Теперь вы легко найдете количество оборотов вокруг монеты с вдвое большим радиусом и вокруг двух монет. 
В названии статьи и разделов использованы (найденные в Интернете) палиндромы - фразы, читающиеся так же и задом наперед, что дает основание считать их дальними родственниками циклоид (©). Придумайте свои палиндромы - увлекательное занятие!

(В журнальном варианте Константин Кноп добавил материал о числовых палиндромах, смотрите об этом Интересные числа)

Добавляю позже. Щелкните здесь - откроется картинка с видами циклоид при разных соотношениях радиусов окружностей, рассмотрите ее, это очень интересно! Скачал с какого-то англоязычного сайта, к сожалению, не помню адреса, спасибо автору, попытаюсь его восстановить