Как обустроить жизнь – советы мудреца Опубликовано в Hard'n'Soft  №5/2002 Cтр. 92

Жизнь - это гонка, где каждый стремится вырваться вперёд, чтобы придти к финишу последним.

Что самое приятное узнали вы в прошедшем двадцатом веке? Разброс ответов может быть широким – полет Гагарина, генетика, Интернет, телевидение, видео и аудиозаписи и т.д. В одной книжке, например, было написано, что пройдут тысячелетия, но ХХ век будут вспоминать из-за восстановления еврейского государства, кто-то на первое место ставит кубик Рубика – то есть, у каждого свои представления о “вековых” ценностях, чаще всего не совпадающие с представлениями даже самых близких друзей, не говоря уже о посторонних. Напоминаю – речь идет о приятном. Рискуя быть обозванным всякими словами, заявляю – самые приятные штучки, которые подарил нам прошлый век – это фракталы, флексагоны и игра “Жизнь”. Напрягите память и фантазию – ничего более приятного вам не найти. О флексагонах и фракталах поговорим позже (99% удовольствия состоит в его предвкушении), нынче звезды благосклонны (и об астрологии поговорим) к разговору о жизни.

Часть 1. Вступление. Жизнь - как телеграмма, короткая и с ошибками!

Сейчас вы прочитаете о замечательной игре, которая так и называется – игра Жизнь. Это не “стрелялка”, не собирание сокровищ и не противоборство с компьютером в привычном понимании игр. Жизнь – это даже не игра, а некоторое моделирование, доступное, занятное и увлекательное для программистов, философов, биологов и просто любителей всяких забав. Впервые рассказ об этой игре появился в книге Мартина Гарднера “Математические досуги” (М.,Мир 1972), а в его же книге “Крестики-нолики” (М.,Мир 1988) приведен материал, обобщающий буквальный шквал находок, появившихся на волне всеобщего увлечения игрой. Популярность её была необычайно высока. Не было ни одного программиста, не писавшего программы для Жизни. Как только появлялось новое оборудование: древние теперь ЕС-ки, СМ-3, СМ-14-20 ДВК, Синклер-Спектрум – на экранах вскоре начинали ползать причудливые организмы. Появление ПК, массовый доступ к ним открывает возможность желающим написать программу для Жизни или, имея такую программу, поиграть с ней.
В книге Ч. Узерелла “Этюды для программистов” (М. Мир 1982) самым первым пунктом идёт предложение написать программу для игры Жизнь. Сам процесс обдумывания нехитрого алгоритма, способа задания колонии клеток и вывод на экран очень полезен для новичков и доставит удовольствие опытным программистам. Но, как выяснилось, пришло новое поколение незнакомое с игрой Жизнь, даже многие программисты не слышали о ней, не говоря уже о школьниках и студентах. Поэтому познакомим их с правилами Жизни.

Прежде надо сказать об авторе. Игру создал Джон Конуэй. Собственно, так называемая теория клеточных автоматов давно известна узкому кругу математиков, но удачные алгоритмы наследования, предложенные Конуэем, сделали его детище необычайно популярным. Вряд ли Конуэй ожидал, что его игра вызовет столь бурный интерес – как в научных кругах, так и среди любителей компьютерных забав. Основная заслуга в этом принадлежала известному популяризатору науки Мартину Гарднеру, опубликовавшему исследования Жизни в журнале “Scintefic American” в начале 70-х годов. Игра состоит в том, чтобы, начав с какого-нибудь простого расположения фишек (организмов) на различных клетках доски, проследить за эволюцией исходной позиции под действием “генетических законов” Конуэя. Законы, напоминающие обычные биологические, управляют рождением, гибелью и выживанием фишек: колония погибает от перенаселённости, то есть слишком большой плотности фишек, или от одиночества (разрозненности фишек) и иногда переходит в стабильный цикл превращений с определённым периодом. Кроме того, должны существовать начальные конфигурации, заведомо обладающие способностью к беспредельному развитию, правда с условием, чтобы было непросто доказать эту “беспредельность”. Необходимо также оговорить кажущиеся расхождения в терминологии – иногда говорят об организме, имея в виду, что он состоит из клеток, меняющихся по законам Конуэя, а иногда говорят об организме, как ячейке крупной колонии организмов, что, в принципе, разные названия одного и того же процесса. Игры, подобные Жизни, прежде разрабатывали и другие математики, но только генетические законы Конуэя позволили найти золотую середину между слишком высокой рождаемостью и смертностью, при которой ход “жизни” можно прослеживать на большую глубину и даже играть вручную.

Часть 2. Напоминание Жизнь такова, какова она есть и больше никакова. Каково?

Напомним, что каждую клетку доски – а доска предполагается в идеальном случае бесконечной – окружают восемь соседних клеток. Законы Конуэя формулируются следующим образом:
Выживание. Каждая фишка, у которой две или три соседки, выживает и переходит в следующее поколение.
Гибель. Фишка, у которой больше трёх соседей, погибает от “перенаселённости” и снимается с доски. Фишка, вокруг которой нет соседей или только одна соседка, - умирает от одиночества.
Рождение. Если число фишек, с которыми граничит какая-нибудь пустая клетка в точности равно трём (не больше и не меньше), то на этой клетке рождается новый организм, то есть следующим ходом на него ставится одна фишка.
Важно понять, что рождение и гибель всех “организмов” происходит одновременно. Вместе взятые они образуют одно поколение, или один ход. Начните игру – расположите на доске произвольную конфигурацию из фишек (можно использовать обычные шашки) и запустите первый шаг жизни, то есть уберите погибших и поставьте родившихся. Потом повторяйте шаги, наблюдая за популяцией. Вскоре после начала игры вы заметите, что популяция всё время претерпевает необычные, нередко очень красивые и всегда неожиданные изменения. Иногда, обычно через большое число поколений, первоначальная колония организмов постепенно вымирает: все фишки исчезают – или, напротив, исходные конфигурации переходят в устойчивые и перестают изменяться (например, блок из четырёх фишек), либо навсегда переходят в колебательный режим. Часто возникающая во время игры колебательная конфигурация – “светофор”, или “мигалка”: три фишки по горизонтали или вертикали. А конфигурации, не обладавшие в начале игры симметрией, обнаруживают тенденцию к переходу в симметричные формы.
Самое интересное, что в Жизни невозможно предсказать результат процессов, которые, казалось бы, жёстко определены чрезвычайно простыми правилами развития. Создавая организм мы не знаем заранее как он будет меняться из поколения в поколение. Это добавляет азарта в поиски удачных конструкций и делает находки особенно привлекательными. При наблюдении смены поколений самых различных организмов бросаются в глаза стабильные или мигающие островки, на которые часто распадается колония. На рисунке можно проследить (слева направо) жизнь мигалки-светофора, улья и трех мигалок (названия предложены в книгах Гарднера)

Целая армия энтузиастов занималась исследованием Жизни. Были исследованы организмы на цилиндрических, сферических, торообразных поверхностях и даже на ленте Мебиуса. Были попытки запустить Жизнь на досках с шестиугольными и треугольными ячейками, вывести жизнь в объем, задав правила жизни в трехмерном мире, и, конечно же, пробовали менять сами правила жизни, то есть число соседей, при котором сохраняется, погибает или рождается клетка. Пробовали разные алгоритмы раскраски и даже запускались организмы разного пола, чтобы посмотреть, как они будут размножаться. Здесь проявляется эффект, подмеченный фантастами, например, Лемом в “Солярисе”. Когда человек сталкивается с новым явлением, то подходит к нему со своими, человеческими мерками. Ну зачем, скажите, клеточным организмам размножаться? Они не читали Фрейда, у них совсем другие цели в их жизни. Может, им приятно мигать, распадаться, двигаться. Есть такая шутка “не надо придавать компьютерам человеческие черты – им это не нравится”. Хочется то же повторить о клеточных организмах. Еще неизвестно, что они думают о нас.
Однако, возвращаюсь к экспериментам, время показало, что самая наглядная Жизнь, самая действующая ее модель для философов, генетиков, химиков, физиков и математиков – это простые алгоритма Конуэя на элементарном клетчатом поле. Именно на эту Жизнь ссылаются многочисленные ученые, философы и публицисты, толкуя о самых разных предметах. Одно из самых замечательных открытий Конуэя – “глайдер”, состоящий из пяти фишек. После второго хода глайдер немного сдвигается и отражается относительно диагонали. В результате двух последующих ходов глайдер выходит из пике и ложится на прежний курс, сдвигаясь на клетку относительно начальной позиции. Открытие глайдера вызвало не только новую волну открытий движущихся конфигураций, но и привлекло к Жизни внимание физиков, усмотревших аналогию с квантами света, с передачей информации и ее приемом. Были также найдены конфигурации, “стреляющие” глайдерами.

В вышеупомянутых книгах Гарднера можно найти множество интересных конфигураций, найденных любителями Жизни: там и комические корабли, выпускающие ракеты, и “пожиратель глайдеров”, и “жнейка”, оставляющая за собой сжатые снопы, и улья и многое другое. При появлении игры возник вопрос – есть ли конфигурации, у которых количество клеток неограниченно возрастает? Открытие ружья, стреляющего глайдерами, дало положительный ответ. А еще позже был открыт ужасный вирус, стремительно заполняющий поле своими ячейками.

Причем его устрашающий вид соответствует агрессивности, через секунду после старта на 88 шагу он состоит уже из 2978 ячеек, и если апплет вовремя не остановить, то…. Находится этот ужас на http://radicaleye.com/lifepage/patterns/contents.html   - специальном собрании интересных конфигураций Жизни. Например, там же, на http://radicaleye.com/lifepage/patterns/hwssgun.html   расположена пушка, стреляющая снарядами.

Теперь, когда вы почти все знаете, повторю самое замечательное качество игры - она является идеальным объектом для программирования: так и не терпится объявить двумерный массивчик и в цикле проверять каждую ячейку на одиночество и на перенаселённость… Предлагаю текст старенькой программы игры Жизнь, написанной на Бейсике. Программа отлажена в Turbo Basic’e, работает также в старичке GWBasic’e и, с небольшими изменениями (убрать отрицательные значения индекса массива) в любимом многими QBasic’e. (Если вы думаете, что у всех стоят Пентиумы четвертые с Windows XP, то напрасно – в школах и институтах изучают Бейсик и Паскаль под ДОС, так что эта программа пригодится для курсовой работы)
10 '=========================LIFE===================
20 CLS : H=17 : L=54 : S$=CHR$(219) : P$=CHR$(250): COL=0 : FON=3
30 COLOR 1,7 : FOR I=1 TO 2160 : ?CHR$(177); : NEXT
40 LOCATE 25,1 : FOR U=1 TO 80 : ?CHR$(177); : NEXT
100 DIM A$(H+5,L+5) ,Z$(H+2,L+2)
120 COLOR COL,FON : FOR I=-1 TO H+1 : FOR J=1 TO L+2 : A$(I,J)=P$
130 A$(-1,J)=CHR$(205) : A$(H+1,J)=CHR$(205)
140 A$(I,1)=CHR$(186) : A$(I,L+2)=CHR$(186) : A$(H+1,L+2)=CHR$(188)
150 A$(-1,1)=CHR$(201) : A$(-1,L+2)=CHR$(187) : A$(H+1,1)=CHR$(200)
160 LOCATE I+3,J+10 : ?A$(I,J) : NEXT J,I
170 COLOR 0,7 :R$=CHR$(178)+CHR$(178) : FOR I=-0 TO H+1 : FOR J=1 TO L+2
180 LOCATE 3+I,L+13 :?R$ : LOCATE H+5,J+11 : ?R$ : NEXT J,I
200'==========================ВВОД====================
210 COLOR 15,5 : LOCATE 23,5 : S=0
220 ?" ВЫХОД- ВЫБОР ПОЛЯ- ЖИЗНЬ- СНОВА-<9> "
250 X=5 : Y=15 : LOCATE Y+1,X+10 : COLOR 31,FON : ? CHR$(206)
300 Q$=INKEY$ : IF Q$="" GOTO 300
310 IF Q$=CHR$(27) THEN SYSTEM
315 IF Q$=CHR$(8) THEN GOTO 2000
320 IF ASC(Q$)=32 THEN GOTO 1000
330 IF ASC(Q$)=57 THEN GOTO 150
350 W$=RIGHT$(Q$,1)
360 IF A$(Y,X)<>S$ THEN LOCATE Y+1,X+10 : COLOR COL,FON : ?P$
400 IF W$="K" THEN X=X-1 : IF X <2 THEN X="X+L" 410 IF W$="M" THEN X="X+1" : IF X> L THEN X=X-L
420 IF W$="H" THEN Y=Y-1 : IF Y <2 THEN Y="Y+H" 430 IF W$="P" THEN Y="Y+1" : IF Y> H+2 THEN Y=Y-H
445 IF A$(Y,X)<>S$ THEN LOCATE Y+1,X+10 : COLOR 31,FON : ? CHR$(206) : GOTO 300
1000 A$(Y,X)=S$ : S=S+1: LOCATE Y+1,X+10 : COLOR COL,FON : ? A$(Y,X) : GOTO 300
2000'==========================ТЕЛО ЦИКЛА===============
2050 S=0 : FOR I=1 TO H:FOR J=1 TO L
2080 A$(0,J)=A$(H,J): A$(H+1,J)=A$(1,J) : A$(I,0)=A$(I,L) : A$(I,L+1)=A$(I,1)
2090 NEXT J,I 2095 FOR I=1 TO H:FOR J=1 TO L :Q=0:Z$(I,J)=P$:IF INKEY$=CHR$(27) THEN END
2097 IF INKEY$="0" THEN GOTO 120
2100 IF A$(I-1,J-1)=S$ THEN Q=Q+1
2150 IF A$(I-1,J)=S$ THEN Q=Q+1
2200 IF A$(I-1,J+1)=S$ THEN Q=Q+1
2250 IF A$(I,J-1)=S$ THEN Q=Q+1
2300 IF A$(I,J+1)=S$ THEN Q=Q+1
2350 IF A$(I+1,J-1)=S$ THEN Q=Q+1
2400 IF A$(I+1,J)=S$ THEN Q=Q+1
2450 IF A$(I+1,J+1)=S$ THEN Q=Q+1
2500 IF A$(I,J)=S$ THEN IF Q=2 OR Q=3 THEN Z$(I,J)=S$ : S=S+1 :GOTO 2900
2550 IF A$(I,J)=S$ THEN IF Q<2 OR Q>3 THEN Z$(I,J)=P$ : GOTO 2900
2600 IF Q=3 THEN Z$(I,J)=S$ : S=S+1 : GOTO 2900
2650 Z$(I,J)=P$
2900 COL=0 : IF Z$(I,J)=A$(I,J) THEN COL=COL+1
2950 COLOR COL,FON : LOCATE I+3,J+11 : ? Z$(I,J) : NEXT J,I
3000'==========================ВЫВОД НА ЭКРАН=========
3050 FOR I=1 TO H : FOR J=1 TO L:A$(I,J)=Z$(I,J) : NEXT J,I
4000'========================ОПРОС====================
4005 IF S=0 THEN COLOR 30,4 : LOCATE 21,10 :?" КОНЕЦ "
4010 COLOR 0,2 : LOCATE 23,2
4020 ?" ВЫХОД- ИЛИ- СНОВА-<0> N=";N;" КОЛ=";S
4060 LOCATE 1,1 :?
4100 M$=INKEY$ : IF M$=CHR$(27) OR M$=CHR$(32) THEN SYSTEM
4200 IF M$="0" THEN GOTO 120
4300 N=N+1 : GOTO 2000 5000 END
После запуска программы появляется игровое поле с курсором, который управляется клавишами со стрелками. При нажатии пробела на месте курсора появляется молекула или организм. Повторяя процедуру строим задуманную конфигурацию и нажимаем Backspace для запуска игры.

Новые организмы, появляющиеся на экране, имеют синий цвет, а старые, бывшие живыми в прошлом шаге цикла – чёрный. На экран выводятся номер цикла и количество организмов в конфигурации. Программа достаточно проста и любой школьник может её улучшить.

Часть 3. Обзор. Что наша жизнь? … Экран!

Если задать в Сети поиск сочетания “игра Жизнь”, то она выловит сотни страничек, так как начинающий программист – владелец странички непременно выкладывает свой вариант игры. Главное, что хочется порекомендовать заинтересовавшимся – Клуб жизнелюбов на http://elvisti.kiev.ua/skl/   основанный редактором Киевского журнала “Компьютеры+программы” Владимиром Скляром (почти однофамилец). Там вы найдете интересные статьи автора странички и других жизнелюбов. Но клуб пару лет не обновляется – сайты тоже (как и клеточные организмы) стареют, поэтому рекомендую лучшую свежую страничку http://famlife.narod.ru/index.html   посвященную одноименной программе-игре и имеющую хорошую коллекцию жизненных ссылок.
Предлагаемая на страничке реализация Жизни одна из самых удачных, имеет много настроек, в том числе пять цветовых схем и возможность менять правила Жизни. Из несущественных недостатков можно указать отсутствие масштабирования и невозможность свернуть окно программы, что затруднило создание скриншота.
Еще одна приятная программа, которая так и называется “Игра жизнь” расположена на http://danila.child.ru/life  и имеет отдельное окно для обзора ситуации и диаграмму изменения количества клеток в популяции.
Самой же хорошей реализацией игры Жизнь, на мой взгляд (и это подтверждается на всех рунетовских и иностранных “жизненных” страничках) является программа Life32 Джона Бонтеса, выложенная на http://psoup.math.wisc.edu/Life32.html .

Игра приятно оформлена и имеет множество настроек, в том числе и позволяет менять правила жизни.  Поиграть можно и в Интернете, много страничек с апплетами, например у школьников-экологов на http://ksch1.narod.ru/life/live.htm   Самая удачная реализация трехмерной Жизни (кроме нас с вами, естественно) расположена на http://www.ipm.sci-nnov.ru/~demidov/Life/Game.htm . Конфигурацию можно вращать мышкой в пространстве, а задавать ячейки удобно – щелкая по шарикам в узлах трехмерной решетки.

Часть 4. Продолжение с философией. Люди не хотят жить – просто они боятся смерти.

Желающим углубленно изучать перекликающиеся с Жизнью вопросы хаоса, самоорганизации, бифуркации, фракталов и другие не менее интересные рекомендую три статьи.
Первая - А.Ю. Лоскутов, д. ф. м. н., проф. МГУ. “Синергетика и нелинейная динамика: новые подходы к старым проблемам” на http://utc.uni-dubna.ru/~mazny/students/site2/ideal_3.htm .
Вторая - С.П.Капица, С.П.Курдюмов, Г.Г.Малинецкий , Синергетика и прогнозы будущего" расположена на http://www.iph.ras.ru:8100/~mifs/kkm/Gl1.htm .
Третья - Клеточные автоматы и игра "Жизнь" расположена на http://www.ctc.msiu.ru/materials/book/5_1_programming/5_1_model/03_life/index.html .

Определенный интерес вызывает статья “Игра "Жизнь" и "компьютерное" представление о мире и Боге” (на http://rusnauka.narod.ru/lib/author/mivmiv/2/   ) в которой авторы “притягивают” игру Жизнь к вопросам квантовой механики, передачи информации и познаваемости мира. Впрочем, авторы честно в введении называют свои гипотезы спекулятивными.

Упражняться в связывании игры Жизнь с вопросами мироздания можно без конца. Известно, что по текущей конфигурации Жизни нельзя однозначно указать предыдущую конфигурацию, так же, как по позиции на шахматной доске нельзя указать предыдущую расстановку фигур. И, в то же время, все шахматные партии начинаются с одной и той же расстановки фигур. Опять же известны конфигурации Жизни, не имеющие предыдущих конфигураций. Поразмышляйте на досуге об этом, об инвариантности прошлого, предопределенности будущего и первоначальной расстановке. Есть гипотезы, согласно которым изменчивость организмов (настоящих, белковых) лишь незначительно зависит от внешней среды, ее направление заложено в самих организмах. Так что мы все с нашей суетой, со всеми хлопотами и интригами возможно лишь модели на чьем-то мониторе.

Хотелось бы отметить, что фотографии колебательных химических процессов (реакция Белоусова-Жаботинского) в статье В.А. Вавилина "Автоколебания в жидкофазных химических системах" ( http://vivovoco.nns.ru/VV/JOURNAL/NATURE/05_00/05_19-25.HTM ) необычайно похожи на движущиеся изображения некоторых алгоритмов работы клеточных автоматов ( http://psoup.math.wisc.edu/mcell/mjcell/mjcell.html ). И сходство это, конечно, не случайно, через клеточные автоматы можно смоделировать распространение эпидемии, атмосферные вихри, социальные и экономические процессы.

Игра Жизнь тесно связана с новым перспективным направлением программирования – генетическими алгоритмами (ГА). Известны, например, работы, когда создавалась колония программ, решающих так называемую задачу коммивояжера (поиска оптимального маршрута между несколькими городами), потом из программ отбирались самые успешно справляющиеся с задачей, программы скрещивались случайным образом, обмениваясь фрагментами кода, снова отбирались и скрещивались… В результате оставались несколько самых “продвинутых” программ. Причем не создавался гений, а “тусовались” какое то количество программ приблизительно одного уровня. Подробности смотрите на http://www.computerra.ru/offline/1999/289/2523/for_print.html . Самое интересное, что часто потомки “успешных” программ работали хуже своих родителей. Это напомнило сетования одного моего знакомого на то, что дети не умнее родителей. Да и все видят, что со времен Архимеда и Пифагора человечество в лучшем случае не поумнело. Вся надежда на ГА. Заинтересовавшимся моделистам рекомендую статью “Популярно о генетических алгоритмах” (на http://saisa.chat.ru/ga/ga-pop.htm ). Перекликается с темой и моя статья “Наследственность у биоморфов”, расположенная на http://www.computerra.ru/offline/2001/401/10791/for_print.htm  

Часть 5. Наладим свою жизнь. Со смехом можно не только продлить жизнь, но и создать новую

Все вышесказанное было вступлением к предложению разделить удовольствие от создания своей модели игры Жизнь и внести свой небольшой вклад в развитие ГА. “– С чего же мы начнем? – С самого начала! – воскликнул Сайрус Смит” (Жюль Верн. “Таинственный остров”. Заметьте, что инженер Сайрус Смит, живший полтора века назад, знал, как сделать порох, варить сталь и еще тысячи сведений, позволивших колонистам создать “технологическое” поселение. Какой ВУЗ он заканчивал?)

Запустим Жизнь на поле с шестиугольными ячейками, что, возможно, позволит получить новые, неизвестные на прямоугольной доске качества. Известны примеры удачного переноса “прямоугольных” игр на шестиугольные поля, например, шахмат (известны несколько вариантов) или “Козлик и Волки”. Главным отличием является количество соседей ячейки – их теперь шесть, а не восемь. Небольшие приятные хлопоты будут связаны со смешением каждого ряда на пол ячейки для получения “сотовой” структуры, причем через один ряды смещаются в одну сторону, а оставшиеся в противоположную. Это же смещение придется учитывать при подсчете соседей ячейки и при выборе ячеек мышкой. Зато у нас сохраняется возможность обработки двумерного массива, что облегчает анализ и рисование поля. То есть, массив прямоугольный, но за счет смещения строк ячейки получаются шестиугольными. Создайте форму в Visual Basic’e, разместите кнопки как на скриншоте, введите текст программы и запускайте свою шестиугольную Жизнь! Нажмите кнопки New и Run, включите флажок Vew last – и вы вскрикнете от восторга – на экране плещется самая настоящая Жизнь!

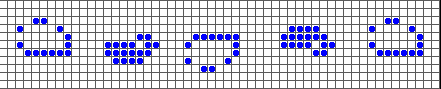
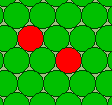
Dim a(40, 40) As Integer, b(40, 40) As Integer, c(40, 40) As Integer Dim radius As Byte, i As Byte, kol As Byte Dim sdvig As Integer, m As Byte, tormoz As Boolean Dim num_cel As Integer, number As Integer, burn As Byte, life As Byte
Private Sub Form_Load()
burn = 2 ' количество соседей для появления новой жизни
life = 3 ' количество соседей для сохранения жизни
num_cel = 1 ' количество ячеек в организме
number = 0 ' номер поколения
radius = 7 ' радиус ячейки в пикселях
kol = 40 ' Количество рядов и ячеек в ряду
tormoz = True ' Признак остановки автоматической смены поколений
DrawWidth = 1 ' Толщина линии
draw_life6 ' Прорисовка экрана
End Sub
' Подпрограмма выбора мышью
Private Sub Form_MouseDown(Button As Integer, Shift As Integer, X As Single, Y As Single) ' Перевод координат щелчка мыши в счетчики циклов
yy = Int((Y - 10) / radius / 1 / 1.7 + 0.5)
xx = Int((X - 60 - radius / 2 * (-1) ^ yy) / radius / 2 + 0.5)
If a(xx, yy) = 1 Then a(xx, yy) = 0 ' Погашение ячейки
Else a(xx, yy) = 1 ' Включение ячейки
End If
number = 0
draw_life6
End Sub
'Подпрограмма рисования поля
Sub draw_life6()
num_cel = 0
For X = 1 To kol
For Y = 1 To kol
sdvig = radius / 2 * (-1) ^ Y ' Сдвиг каждого ряда то влево, то вправо
X1 = 60 + X * radius * 2 + sdvig
Y1 = 10 + Y * radius * 1.7
FillStyle = 0
If a(X, Y) > 0 Then FillColor = RGB(255, 0, 100) ' Цвет заливки пустой ячейки
Else FillColor = RGB(50, 150, 0) ' Цвет заливки активной ячейки
End If
If c(X, Y) <> 0 And Vew_last.Value = 1 Then FillColor = RGB(150, 50, 50) ' Цвет предыдущей
Circle (X1, Y1), radius, RGB(0, 55, 0)
num_cel = num_cel + a(X, Y)
c(X, Y) = a(X, Y)
Next Y
Next X
Line (21, 233)-(45, 246), RGB(255, 255, 255), BF
Line (13, 272)-(32, 285), RGB(255, 255, 255), BF
PSet (-1, 220)
Print " Step ": Print " №"; number Print Print "Num of cells": Print " "; num_cel
End Sub 'Подпрограмма вывода случайной конфигурации
Private Sub New_Click()
For X = 1 To kol: For Y = 1 To kol
a(X, Y) = 0: Next Y: Next X
For i = 1 To 10: a(Int(Rnd * 5 + kol / 2), Int(Rnd * 5 + kol / 2)) = 1: Next i
number = 1
draw_life6
End Sub
' Подпрограмма автоматической смены поколений
Private Sub Run_Click()
Do While tormoz = True
analiz
draw_life6
DoEvents
'For j = 1 To 10: qq = 999 ^ 4 + qq: Next j ' Для задержки....
Loop tormoz = True End Sub ' Подпрограмма пошаговой смены поколений
Private Sub Go_Click()
analiz
draw_life6
End Sub ' Выход из программы
Private Sub Exit_Click()
End
End Sub
' Подпрограмма анализа конфигурации и смены поколения
Private Sub analiz()
For X = 2 To kol - 1
For Y = 2 To kol - 1
m = 0 ' счетчик активных соседних ячеек
sdvig = (-1) ^ Y ' с учетом сдвига рядов
m = m + a(X - 1, Y)
m = m + a(X + 1, Y)
If sdvig <0 Then
m="m" + a(X 1, Y + 1)
m="m" + a(X 1, Y 1)
Else m="m" + a(X + 1, Y + 1)
m="m" + a(X + 1, Y 1)
End If
m="m" + a(X, Y + 1)
m="m" + a(X, Y 1)
If a(X, Y)="1" Then ' Для активной ячейки
If m="life" Then ' Условие сохранения активности
b(X, Y)="1" ' вспомогательный массив
Else b(X, Y)="0" ' смерть активной ячейки
End If
Else ' для пустой ячейки
If m="burn" Then b(X, Y)="1" ' Условие рождения активной ячейки
Else b(X, Y)="0" ' Осталась пустой
End If
End If
Next Y
Next X
For X="1" To kol
For Y="1" To kol
a(X, Y)="b(X," Y) ' Перекидка вспомогательного массива в основной
b(X, Y)="0" ' очистка
Next Y, X
number="number" + 1
End Sub
' Подпрограмма остановки автоматической смены поколений
Private Sub Stop_Click()
tormoz="False"
End Sub

Организм можно задать щелкая мышкой по полю или нажав кнопку “New”, что вызовет появление случайной конфигурации. Запускать процесс можно пошагово (кнопка “Go”) или в автоматическом режиме (“Run”), можно выводить предыдущее поколение ячеек для красоты. Но все это украшательство процесса, а сердцевина его сосредоточена в выборе основных параметров – количества соседей, при котором активная ячейка остается активной (переменная life) и количества активных соседей, при котором в пустой ячейке зарождается жизнь (переменная burn). Длительные эксперименты выявили оптимальные значения для них 3 и 2 соответственно. При этих значениях многие конфигурации живут до нескольких десятков поколений. Выявлены интересные устойчивые колеблющиеся конфигурации, которыми и заканчивается обычно Жизненный путь. Мигают оставшиеся рядом две ячейки.

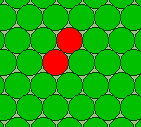
А из трех ячеек получается две мигалки – пульсирующий треугольник в верхнем ряду и вертушка в нижнем ряду картинки.

Существует мигалка трехступенчатая, в которой шестиугольник иногда становится снежинкой.

Существует мигалка и из четырех ячеек, предлагаю читателям найти ее и тем самым попасть на Арбузную доску почета. Изменение значений “правил Жизни” меняет режим протекание процесса. Если назначить life=2 и/или burn=3 (или burn=4), то колония довольно быстро погибает. Если же задать оба параметра равными двум, то колония быстро разрастается по всему полю, может, это и не плохо для нее, но для нас не так интересно. Может быть существуют другие интересные сочетания параметров? Начните новую Жизнь, не пожалеете. Кто знает, может фишки Жизни, при достаточно длительном и удачном эксперименте, организуются и осознают себя – возможно, даже начав общаться с нами, создателями. А может, всё наоборот, - и мы всего лишь фишки в чьей-то игре?…