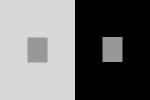Алгоритмы инопланетной геометрии

В последнее время в средствах массовой информации все чаще мелькают сообщения о загадочных кругах и более сложных фигурах, которые неведомо откуда появляются за одну ночь на пшеничных полях по всему миру. Особенно инопланетяне разгулялись в Англии. Фермеры уже всерьез подсчитывают убытки, понесенные ими от бурной аномальной активности. А недавно "Комсомольская правда" (см. "КП" от 24 августа 2001 года www.kp.ru) сообщила о том, что летающие тарелки куролесят уже и на полях в Подмосковье. Скептики склонны относить эти явления к проделкам шутников. Однако объемы, сроки появления и качество этих "произведений" заставляет все же усомниться в справедливости "шуточной" версии. Я глубоко убежден, что вся экстро-, астро-, уфология - это на 99,9999…% полнейший бред и шарлатанство. Однако факты остаются фактами. Я, может быть, тоже отнес бы загадочные круги на полях к очередной фальшивке или проделкам шутников, если бы не наблюдал нечто подобное собственными глазами.

Осенью 1994 года мне случилось летать на Дальний Восток в краткосрочную командировку рейсом "Минск-Омск-Чита-Владивосток". По дороге туда участок пути от Читы до Владивостока мы преодолевали при ярком солнечном свете и ясной погоде. Под лайнером, пока хватало глаза, раскинулось абсолютно дикое, безлюдное пространство. В обратный путь из Владивостока наш "Ту" вылетел поздно вечером. Большинство пассажиров по прошествии получаса полета уже дремало. Мне не спалось, и я вглядывался в темную бездну, лежащую под нами. Вдруг я заметил на земле совершенно правильную, как будто начерченную циркулем светящуюся окружность. Затем еще одну и еще, и еще. Окружности были разных диаметров. Некоторые пересекались между собой и в месте пересечения светящиеся контуры исчезали. Возможно, в совокупности они образовывали какие-то геометрические фигуры, но в тот момент я не подумал о том, чтобы сопоставить их взаимное расположение. Меня, как человека, привыкшего мыслить алгоритмическими категориями, прежде всего интересовало другое: каков алгоритм этого явления. Первое, что пришло в голову - лесные пожары. Может быть, огонь, распространяясь от очага возгорания равномерно во все стороны, образовал эти светящиеся кольца. Версию, однако, сразу же пришлось отбросить, поскольку, во-первых, границы окружностей светились равномерным холодным голубоватым светом, а во-вторых, погода была достаточно влажная, и, пролетая несколько дней назад над этими же местами, я обратил внимание на то, что среди зелени во многих местах поблескивает вода. Версию об антропогенной деятельности также пришлось отбросить. Совершенно непонятно, кому и зачем понадобится забираться на сотни километров в непроходимые дебри для того, чтобы непонятно как и зачем устанавливать там огромное количество лампочек. Я растолкал дремавшего рядом знакомого летчика и спросил, видел ли он что-либо подобное раньше. Он посмотрел на круги и сказал, что ничего подобного раньше не видел, но на скорость и летные характеристики машины это не влияет, поэтому не стоит забивать себе голову, и снова заснул. Это явление долго не выходило у меня из головы. Сама собой напрашивалась версия о посадочных сигнальных огнях для инопланетных летающих тарелок или сверхсекретных военных экспериментах. Однажды, просматривая одну умную книжку (Шариков К.Е. Живой организм и окружающая среда. - Мн.: Ураджай, 1987. - 168 с.), я наткнулся на описание схожего явления, которое называется ведьмиными, или магическими, кругами. Как оказалось, это явление известно уже очень давно. Его механизм долгое время оставался загадкой, но уже более ста пятидесяти лет назад стало известно, что причиной возникновения идеально правильных магических кругов являются… грибы. Спора, попадая в почву, дает начало росту грибнице, которая равномерно растет во все стороны. По краям грибницы появляются плодовые тела со шляпками - это то, что мы называем грибами. На следующий год радиус круга увеличивается, и весь процесс повторяется. Круги образуют шампиньоны, мухоморы, дождевики, лисички, рыжики и др. грибы. Почва внутри круга обедняется влагой и питательными веществами. Поэтому растительность внутри грибных колец полегает. По всей видимости, именно такой круг на поле подмосковного фермера и изображен на фотографии в "Комсомольской правде" (фото 1).

Фото 1

В Европе грибные кольца имеют диаметр в пределах десятков метров, а в диких местах, например, в тайге или прериях Южной Америки, грибные круги достигают гораздо больших размеров, измеряемых сотнями метров. При этом возраст такого грибного суперорганизма может достигать 500-800 лет! Многие грибы содержат особое вещество - люциферин. При взаимодействии с кислородом люциферин испускает то самое свечение, которое я, вероятно, и наблюдал с борта самолета.

На первый взгляд, кажется трудно объяснимым и тот факт, что стебли в кругах на полях лежат почти идеально ровно и направлены в одну сторону. Однако, проанализировав этот феномен с точки зрения современной синергетики, легко убедиться в том, что иначе и не может быть. Такое явление весьма характерно для коллективных кооперативных систем. Представьте себе, что наступило время, когда растения внутри круга уже достаточно ослаблены и готовы упасть. Напомним, что колоски на поле - это генетически однородная популяция организмов, и соответствующая стадия наступает примерно одновременно у всех растений. Какая-то незначительная флуктуация, например, порыв ветра, запускает процесс полегания, который принимает сразу же лавинообразный характер. Падающие стебельки увлекают друг друга наподобие эффекта домино. Происходит, выражаясь языком современной физики, спонтанное нарушение симметрии. Поток падающих стебельков самоорганизуется и становится взаимосогласованным. Крайние падающие стебельки взаимодействуют с соседними, крепко стоящими растениями, и немного откланяются при падении, корректируя вектор падения всех остальных и заворачивая весь поток в правильное кольцо.

Фигуры, появляющиеся на полях Англии и других точках планеты (см. галерею оригиналов на www.2do.ru/map/cropc/bestcat.jpg), гораздо более сложны и изысканны, чем просто круги. Хотя в основе большинства из них лежит тот же базовый элемент - окружность. Если все же это дело рук инопланетян, то они наверняка знакомы с системой полярных координат, циклами и рекурсией. Коллекция загадочных гигантских инопланетных криптограмм запросто могла бы составить основу задачника по курсу программирования на Бейсике под названием "Введение в алгоритмизацию с основами компьютерной графики". Например, криптограмма около г. Эйвбери (фото 2, оригинал на x-files.hobby.lv/real/fields.htm), имеет прямое отношение к темам моих предыдущих публикаций о фракталах и рекурсии.

Фото 2

Возможно, изучая алгоритмы, по которым построены эти фигуры, мы могли бы лучше понять тех, кто пилотирует создающие их летающие тарелки. Представляется, однако, что для того, чтобы нас по-настоящему удивить, они могли бы запрограммировать свои компьютеры на изображение чего-то более сногсшибательного, чем остроумные графические головоломки. Впрочем, и это более вероятно, механизм возникновения загадочных геометрических построений на полях злаковых культур связан все же с какими-то земными процессами. Не исключено, что эти фигуры образуют все те же грибы или какие-то иные колониальные микроорганизмы. В пользу этой версии говорит и тот факт, что растения, взятые внутри кругов, действительно сильно отличаются от нормальных контрольных колосков (см. фото 3, оригинал на astrofobia.narod.ru/par_rou_main.htm).

Фото 3

Колонии микроорганизмов могут достигать гигантских размеров, и в них могут происходить внутренние самоорганизационные процессы, приводящие к образованию симметричных и поразительно красивых макроскопических структур.

Впрочем, я не имею ничего против инопланетян. Более того, я практически убежден в том, что мы не одиноки в космосе. В пользу предположения о том, что Вселенная обитаема и земная биосфера - не единственное проявление феномена жизни в мировом пространстве, говорит простое вероятностное рассуждение. Коль скоро жизнь на земле существует, а этот факт не подлежит сомнению, то, следовательно, вероятность возникновения жизни на планете, вращающейся вокруг звезды типа Солнца, отлична от нуля. Во Вселенной имеются мириады звезд, в том числе огромное множество солнцеподобных светил. Существование планетных систем даже у ближайших к Солнцу звезд - также экспериментально установленный факт. Таким образом, и вероятность образования планетных систем также отлична от нуля. Существуют, кроме этого, ненулевая вероятность возникновения жизни на планетах, обогреваемых своими звездами. Следовательно, с точки зрения теории вероятности по мере роста числа испытаний будет расти и число успехов, сколь бы не была мала вероятность успеха в единичном испытании. Объемы Вселенной таковы, что позволяют говорить о почти неограниченном числе испытаний. Следовательно, с вероятностью, близкой к единице, можно утверждать, что число успехов, то есть обитаемых планет во Вселенной, отлично от единицы.

Крайне трудно представить себе, в каких конкретных формах может быть воплощена инопланетная жизнь. Можно лишь утверждать, что она почти наверняка существует. Какие бы конкретные воплощения она не имела, можно с высокой долей достоверности утверждать, что она будет сформирована в результате длительного эволюционного процесса. Следовательно, общие принципы организации инопланетных биологических структур будут сходны с земными. То есть, эти структуры будут сложными, и в них, как и в земных организмах, наверняка должны будут присутствовать квазифрактарные схемы строения, а при их сборке будут наверняка задействованы некие рекурсивные процедуры.

Трудно предположить, насколько часто живые структуры во Вселенной становятся носителями Y-свойств, то есть, иначе говоря, как часто во Вселенной встречается не просто жизнь, но жизнь осмысленная или разумная. Одно лишь можно утверждать с достаточной степенью уверенности: если встреча землян с инопланетным разумом все же когда-либо состоится, то его носители будут иметь сложные, совершенные, а значит, и красивые формы, а их мир будет не менее сложен и прекрасен, чем наш собственный.

А. КОЛЕСНИКОВ,
Andr61@mail.ru

Генеалогические деревья

Вам никогда не приходила в голову мысль построить свое генеалогическое дерево? Смею утверждать, что да, потому что уже неоднократно заводил разговор на эту тему со многими людьми и всегда слышал положительный ответ и встречал живой интерес к этой теме. Причем особенно эти мысли посещают тех, кому уже перевалило за тридцать. (Но, может быть, это мне показалось.) В основном ответы были типа "Да, приходила неоднократно, но до дела так и не дошло" или "Да, я даже нарисовал дерево на бумаге - родителей, дедов...". А потом я задавал следующий вопрос: "А не пытались ли вы построить вообще схему всей своей родни?" В ответ на лице собеседника всегда появлялась попытка представить, как это вообще можно сделать, после этого следовал ответ, что нет. Оказывается, сделать это можно. Но начнем по порядку.

Было это дело прошлым летом. Нужно мне было расписать довольно громоздкий алгоритм расчета стоимости транзитных транспортировок. Не знаю, как у вас, а мне легче писать программу, когда созревает образное, визуальное представление того, что нужно сделать. Вот для этого и решил я написать небольшую утилиту, чтобы быстро манипулировать древовидной структурой и с удобством ее обозревать. Заготовка была сделана, и началось наполнение дерева данными. Но дальше оказалось, что алгоритм в своей глубине становился сетевым, действовать пришлось по-другому, а заготовка утилиты была брошена и осталась валяться на винчестере.

Специально заниматься вопросами генеалогии мне никогда не приходилось. Но мысль о построении генеалогического дерева также посещала меня неоднократно, причем ясно было, что при этом получается древовидная структура. В принципе, такую структуру можно сформировать в виде папок с помощью обычного Проводника Windows. Но вряд ли кому-то захочется иметь такое хозяйство на винчестере, а программ, более подходящих для этой цели, я не искал. И вот накануне нового года меня вдруг посетила идея насчет того, чтобы применить оставшуюся заготовку для этих целей. За час она была причесана, и я приступил к построению дерева.

Давайте рассмотрим, как построить дерево. Я позволю себе взять выдуманные фигуры для иллюстрации, так что если будет какое-то совпадение с реальными именами (и прочая) читателей - прошу извинить.

Первым узлом вносим туда того человека, от которого, собственно, и строим дерево. Затем добавляем подузел "Родители" и к нему - подузлы с информацией о родителях - фамилия, девичья фамилия, имя, отчество, а также подузел "Братья и сестры" с соответствующими подузлами (см. рис.).

Далее строим нисходящие ветви - родители родителей и их братья и сестры, родители родителей родителей и так далее, насколько хватит данных.

Удобным оказалось то, что с помощью программы легко модифицировать структуру, раскрывать/закрывать требуемые ветви. Сразу стали очевидны информационные пробелы, и я стал выяснять подробности, пару вечеров сидел на телефоне, беседовал с родственниками и выяснял. Все родственники живо откликались и помогали, насколько могли помочь.

К сожалению, много информации оказалось утрачено, тех, кто ею владел, уже не осталось в живых или не осталось здравой памяти у тех, кто еще остался жив. Так что рекомендую начинать выяснять данные о роде пораньше, не упускайте время. Потому что информационный источник, если он еще сохранился, может иссякнуть в любое и при этом самое неподходящее время. Такова жизнь. Альтернатива тогда одна - копание в архивах. Но у большинства на это не хватит ни времени, ни решимости. Мой дядя как-то проводил такую работу. Скажем прямо - это вам не на компьютере работать. Все бумажки, бумажки и ручками, ручками... И то, если архивы сохранились.

Кстати говоря, родственники просили показать результаты моей деятельности. Так что, как водится, программе недоставало умения напечатать дерево на бумаге. Еще немного усилий - и вот дерево можно печатать полностью или начиная с какого-то узла, с рекурсией по всем ветвям или так, как дерево раскрыто на экране. В результате получилась пусть и небольшая, но завершенная программа "Построитель деревьев" (на оригинальность названия не претендую).

Нужно обратить внимание на то, что, кроме нисходящих ветвей "Родители", появились ветви "Братья и сестры", которые явно боковые. Поначалу они появились для полноты информации. Следующей хорошей мыслью было дальнейшее развитие боковых ветвей. К каждому из братьев (сестер) строим подузлы "Муж (жена)" и "Дети" (Рис. 2). Далее проделываем ту же работу для нисходящих ветвей, т.е. родителей, дедов и т.д. Если есть необходимость, то можно добавлять узлы "Муж2 (Жена2)", "Дети2". Как вы догадываетесь, это связано со вторым браком. Результатом этого оказывается примечательный результат - выстраивается структура всей родни. Дальше, если есть желание и потребность, можно добавлять узлы и других видов отношений типа "Кум (Кума)", "Друг (Подруга)" и т.д.

Полученные деревья можно сохранить (и, естественно, загрузить) на диске в виде текстового файла.

Следует отметить, что построение генеалогического дерева открывает такие интересные стороны из жизни рода, о которых никогда ранее не задумывался или которые в силу тех или иных причин не задерживались в памяти, поскольку были оторваны от общего генеалогического контекста. Так что эта работа, на мой взгляд, очень полезна и в познавательном, и в духовном плане.

Возможно, кому-то такая схема представления покажется недостаточно строгой, но если ставить во главу угла результат, то он, на мой взгляд, налицо. Единственная трудность в представлении возникает тогда, когда род расходится, а в нижних коленах где-то сходится, то есть образуется сетевая структура. Однако это встречается, наверно, не так часто и не более, чем в одном экземпляре на человека, от которого строится дерево, так что с этим мириться вполне можно.

Редакция газеты с интересом отнеслась к описываемой теме и любезно предоставила возможность разместить архив программы "Построитель деревьев" для свободного скачивания на своем сайте (www.kv.minsk.by/files/tb.zip).

Возможно, существуют и другие аспекты построения генеалогических деревьев. Кроме этого, в жизни существует множество объектов, которые представляются в виде деревьев, поэтому очень вероятно использование программы и для других целей. Если захотите, пишите мне об этом. Буду рад.

Юрий А. СМАНЦЕР,
georgesman@mail.ru

Еще раз об арифметике и календаре

Я очень признателен коллегам, внимательно ознакомившимся с моей статьей на арифметическую тему и приславшим свои замечания и дополнения. Не буду настаивать на том, что в реальной жизни замена логической условной конструкции на арифметическое выражение всегда однозначно целесообразна и желательна. Отнюдь нет. Интересна сама такая возможность с точки зрения компактификации и универсализации программного кода. В сверхкритичных по временному фактору программах этот вопрос следует изучать и решать особо.

В программе вычисления следующей даты, приведенной в статье, для переменной y (год) не случайно объявлен интервальный тип year от 1990 до 2000. (В текст статьи, правда, включен рабочий вариант программы, в котором тип year создан, но переменная y объявлена стандартным типом, чтобы не вводить всякий раз полностью четырехзначное число 199*). В этом временном промежутке все формулы будут давать правильный результат в 100% случаев. Если вести речь обо всем периоде христианского летоисчисления, то, действительно, необходимо учитывать некоторые нюансы. Алгоритм, приведенный Вадимом Нарейко, отражает поправку, предложенную Луиджи Лилио в середине XVI столетия. Ее суть заключалась в том, чтобы вернуть на место день весеннего равноденствия, изъяв 10 лишних дней, и не вводить дополнительные дни в конце трех веков, номер которых не кратен четырем, а именно: в 1700, 1800 и 1900 годах. Забавный парадокс состоит в том, что в пределах 2000 минувших лет нашей эры алгоритм, учитывающий поправку Лилио, даст 12 ошибочных результатов, а формула, приведенная в статье, лишь 3. При создании универсальных алгоритмов расчета календарных дат на длительные интервалы времени следует учитывать то обстоятельство, что календарь - вещь не только, а может и не столько арифметическая, сколько историческая. Поправка Лилио была введена лишь в 1582 году. До этого времени на протяжении шестнадцати столетий в западных странах каждый четвертый год был високосным. Для того, чтобы вернуть дату весеннего равноденствия на 21 марта, специально созданной римским папой Григорием XIII комиссией было решено изъять из 1582 года десять дней. Папская булла от 24 февраля 1582 года предписывала во всех христианских странах исключить из указанного года десять дней от 5 до 14 октября включительно. Этот исторический факт также необходимо учесть, создавая универсальную программу для расчета следующей даты на длительный период времени. (Кроме того, есть еще и Россия...) Что касается будущего, то использовать правило Лилио (то есть считать невисокосными "вековые" (кратные 100) года, не кратные четырем, можно будет лишь при условии, что мир и в следующем тысячелетии по-прежнему будет пользоваться григорианским календарем. Последнее обстоятельство, кстати, крайне маловероятно, ведь из-за очевидных неудобств существующей системы разработка альтернативных моделей календарей ведется полным ходом уже сейчас. Вообще затронутая тема крайне интересна и особенно в настоящее время, на рубеже тысячелетий, в том числе в связи с проблемой (или псевдопроблемой?) "2000". А есть еще и проблема определения даты пасхи... О календарь в разное время ломали зубы и головы величайшие умы человечества. Поэтому целиком поддерживаю идею продолжения обсуждения календарных проблем и конкурса "Формула - февраль".

А.КОЛЕСНИКОВ

Рекурсия - это просто

Сегодня мы продолжим разговор о классических методах программирования. В этой статье попытаемся обсудить такую технологию построения алгоритмов как рекурсия. Некоторые уже наверняка сталкивались с этим понятием, но, испуганные непонятными кусками кода или непривычностью идеи, поспешили забыть все увиденное и услышанное, надеясь вернуться к этому вопросу позже, и чем позже - тем лучше. Не спешите отложить эту статью, потому как, во-первых, рекурсия - это ДЕЙСТВИТЕЛЬНО просто, во-вторых, рекурсия относится к той группе методов, не зная которых, грамотно программировать НЕВОЗМОЖНО, и чем дольше вы прячетесь от нее, тем хуже.

Итак, не откладывая в долгий ящик, дадим наше первое рекурсивное определение. Мы опишем, используя рекурсию, функцию факториал (напомню, N!=1·2·...·N). Пример выбран не случайно - именно математики придумали рекурсию, а использовалась она для описания числовых последовательностей, следующие значения которых можно найти по предыдущим (такие последовательности называют рекуррентными).

Рекурсивное определение факториала:

1. 0! = 1

2. N!=N·(N-1)!

Итак, дело сделано. Теперь осталось выяснить, что обозначает приведенная запись. C первым пунктом все ясно - он просто явно задает результат вычисления 0! (а именно - 1). Подобное явное задание значений (или действий) на определенных входных параметрах (в данном случае - числе 0) называют условием выхода из рекурсии. Теперь попытаемся понять, что означает вторая запись. Правая часть равенства говорит о том, что функция ! (т.е. факториал) вычисляется для произвольного аргумента N. Правая часть содержит произведение. Первый множитель - само число N, второй - значение, которое функция принимает для N-1. Убедимся, что произведение этих величин действительно дает желаемый результат. Например, 4!=24=4·3! . Теперь разберемся, как вычислять по таким формулам.

Чтобы не затягивать процедуру, попытаемся найти факториал трех. Понятно, что первое выражение ничего нам не даст - оно может помочь вычислить только 0!. Поэтому воспользуемся вторым. Теперь самый важный момент - для вычисления 3! по второй формуле необходимо вычислить 2!. Для вычисления 2! (как и для вычисления 1! на следующем шаге) воспользуемся той же формулой. Получим следующую последовательность вызовов:

1. 3!=3·2!

2. 2!=2·1!

3. 1!=1·0!

0! задано явно, и у нас нет необходимости выполнять рекурсивный вызов для его вычисления (теперь понятно, почему первое выражение называют условием выхода из рекурсии). Зная 0!, последовательно находим 1!,2! и 3!. Обратите внимание на то, что если бы мы не задали условие выхода, алгоритм бы зациклился.

Теперь разберемся, как рекурсия программируется. Сразу хочется обратить внимание, что рекурсия неразрывно связана с понятием подпрограммы (процедуры или функции). На всех современных алгоритмических языках с рекурсивным оформлением подпрограмм не возникает никаких проблем, но обладатели некоторых устаревших версий Бейсика не смогут воспользоваться материалом этой статьи. Единственный совет в таком случае - перейти на что-нибудь посовременней (в Quick и Turbo Basic с рекурсией проблем не возникает).

Пример с факториалом показателен для обучения, но совершенно не годится для программирования, поскольку вычислять факториал рекурсивно крайне неэффективно - лучше воспользоваться классическим циклом for. Поэтому мы выберем другой пример - возведение в степень по алгоритму, приведенному в моей предыдущей статье (те, кто ее не читал - не расстраивайтесь, здесь будет приведено достаточно информации для понимания алгоритма, просто придется немного подумать). Если вы уже пытались запрограммировать его при помощи циклических вычислений, то наверняка поняли, что это не самая простая задача. Приведем алгоритм еще раз, а затем посмотрим, как элегантно все выглядит в рекурсивном стиле.

1. a⁰=1 (условие выхода).

2. если a - четное, то a^x=(a²)^(x/2)

3. если a - нечетное, то a^x=a·(a²)^((x-1)/2)

Рекурсивная процедура просто дословно повторяет алгоритм !

function power(a:longint;x:word):longint;
 begin
 if x=0 then power:=1
 else if x mod 2 = 0 then power:=power(sqr(a),x div 2)
 else power:=a*power(sqr(a),x div 2);
 end; 

Но даже и это - не самый удачный пример рекурсии, поскольку здесь все же можно обойтись циклическими вычислениями. Приведу классический пример задачи, эффективно решить которую помогает только рекурсия.

Речь идет о головоломке "Ханойские башни". Правила ее таковы. Имеется три стержня, на первом из них надето n дисков разного размера, причем нижнее кольцо - самое большое, следующее - чуть меньше и т.д. до самого маленького наверху. Требуется переложить все диски с первого стержня (источника) на третий (приемник), используя второй как промежуточный и придерживаясь следующих правил: за один раз можно брать только один диск и больший диск нельзя класть на меньший.

Можете самостоятельно подумать, как решить задачу при помощи циклических вычислений (алгоритм, мягко говоря, не очевиден, сложен и на практике никогда не используется). При помощи рекурсии задача решается элементарно:

1) если башня состоит из 0 дисков, ничего не делать;

2) иначе, если башня состоит из n>0 дисков, проделать следующие действия:

a) переложить башню из n-1 дисков на промежуточный стержень в качестве приемника;

b) переложить диск с источника на приемник;

c) переложить башню из n-1 дисков с промежуточного стержня на приемник.

Процедура, распечатывающая последовательность перемещений, и в данном случае дословно повторяет словесный алгоритм:

procedure Hanoi (Source, Destination, Temp : char; Count : byte);
 begin
 if Count>0 then
 begin
 Hanoi (Source, Temp, Destination, Count-1);
 Write (Source,'->', Destination,' ');
 Hanoi (Temp, Destination, Source, Count-1);
 end;
 end;

Вызовите процедуру, например, так: Hanoi ('1', '3', '2', 3) и просмотрите последовательность перемещений для трех дисков.

В заключение сделаю несколько общих (но очень важных) замечаний. Любой итерационный процесс можно заменить рекурсивным (подумайте, как), но не всегда стоит это проделывать (вспомните случай с факториалом). Многие рекурсивные подпрограммы можно заменить циклическими вычислениями, но при такой замене они, как правило, разрастаются и становятся малопонятными. В общем случае, рекурсия может быть успешно применена (и применяется) для обработки объектов, части которых имеют тот же тип, что и сам объект (любая часть дерева - дерево, любая часть массива - массив и т.п.). Следует обращать особое внимание на условие выхода, если оно задано некорректно, подпрограмма зациклится. Другая важная вещь - глубина рекурсии, то есть количество вызовов подпрограммой самой себя до срабатывания условия выхода. При каждом вызове подпрограммы занимается часть системного стека, так что если вы проделываете слишком много вложенных вызовов, он переполняется. Не передавайте рекурсивным процедурам громоздкие объекты (массивы и т.п.). Для обработки таких структур либо объявляйте их глобально, а передавайте индексы, либо размещайте их в памяти динамически, а передавайте указатель (в Бейсике могут возникнуть проблемы с этим способом). Устанавливайте большой размер стека, но если это не помогает - скорее всего ваш алгоритм далек от удачного; переделайте его. Для того, чтобы быстрее овладеть методом, старайтесь найти рекурсивное решение всех задач, предполагающих циклические вычисления, а затем разбирайтесь, какое решение эффективней (в большинстве таких случаев цикл все же лучше).

Постарайтесь овладеть рекурсией в совершенстве - без нее многое (например, работа с деревьями) становится практически невозможным.

Денис МАРГОЛИН,
margolindenis@usa.net

Технологии иллюзий

То, что раньше считалось иллюзорным, как говорится, в диковинку, сегодня находит широкое применение во многих отраслях и сферах деятельности человека. Иллюзия - обман, базирующийся на человеческих слабостях, и самая главная наша слабость - стереотипы. Иллюзия заставляет срабатывать стереотипы, вызывая смех или удовольствие ее создавшего. С другой стороны, иллюзия - жанр, в котором есть первопроходцы и продолжатели. Сегодня нельзя сказать, когда появилась впервые эмуляция 3D на плоскости, кто придумал боевики и сколько лет первому "красивому" обману. А причиной тому - неуемная человеческая фантазия.

Да, мы на протяжении нескольких номеров будем говорить об иллюзиях, о том, как они пришли в наш мир и где применяются. В последней статье данного небольшого цикла я размещу ссылки на ресурсы, которые использовал при его создании. А сейчас давайте начнем знакомиться со знаменитыми иллюзиями.

Самая знаменитая иллюзия - лицо девушки-старушки

Эта картинка, пожалуй, знакома многим. Посмотрите внимательно, кого вы видите: девушку или старушку? Девушка имеет свои контуры, старушка - свои. Глаз старушки и ухо девушки - один и тот же элемент, но при разных вариантах видения это не заметно. Честно сказать, девушку я увидел не сразу, а только через день после первого просмотра. Для тех, кто не увидел, скажу, что контур лица девушки - это контур носа старушки.

В этом, 2000-м, году картине исполняется 85 лет с момента первой публикации в 1915 году английским карикатуристом У.И.Хиллом. Хилл адаптировал в данном рисунке концепцию, которая уже была популярна в то время в индустрии развлечений: "Вы видите мою жену, а где же моя теща?". Причем первые подобные рисунки уже ходили в мире задолго до того - в 1888 и в 1890 годах были представлены похожие работы. С тех пор к данной концепции возвращались много раз. Например, в 1961 году Дж. Ботвиник переделал рисунок под "Муж и тесть".

После внимательного изучения данных рисунков я стал искать современные работы в этом направлении. Казалось бы, сейчас у нас есть такой мощный инструмент, как компьютер… Но так получилось, что ни с использованием фотомонтажа, ни с другими производственными технологиями данное представление иллюзии не нашло своего продолжения сегодня. Почему, интересно?

Невероятная лестница

На рисунке представлена разработка Лайонела Пенроуза, получившая в дальнейшем название "Невероятная лестница". Попробуйте ткнуть стержнем ручки в разные области рисунка или же подвести курсор мыши, если вы читаете интернет-вариант. Ощущение разной высоты присутствует? Это специально разработанная многоуровневая физическая модель, причем единственная в мире по своей оригинальности. Разработка Л.Пенроуза легла в основу знаменитой картины М.К. Эшера "Ascending and Descending" (что на русский можно перевести примерно как "Восхождение и Спуск").Помимо графического искусства, физическая многоуровневая модель, представленная и популяризированная М.К.Эшером, Лайонелом и Роджером Пенроузами, нашла свое отражение и в музыке. В 1964 году психолог Роджер Шепард изобрел аудио-иллюзию, используя диатонику от Cmaj в диапазоне четырех октав. Сейчас эту музыкальную иллюзию создают с помощью синтезаторов и компьютеров. Но для того, чтобы суметь ее правильно сыграть, нужен, конечно, опыт и специальные тренировки. Сегодня, например, вы можете купить CD с музыкальными иллюзиями на сайте Д.Дойче из Университета Сан-Диего.

Думаю, что все это - еще только начало применения физической модели "невероятной лестницы" во многих областях искусства.

Комната Амеса

Изобретение названо в честь реализовавшего его Адельберта Амеса-младшего, офтальмолога (США). Он впервые сконструировал свою комнату в 1946 году. Данный дизайн создан на основе представлений от Г.Гельмгольтца, ведущих свое начало еще в 19-м веке.

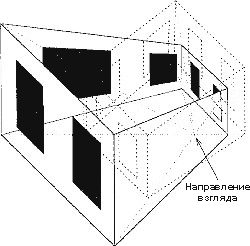
В комнате Амеса представлены совместно две иллюзии. Первая - то, что комната выглядит кубической, хотя на самом деле она трапецеидальная, вторая заключается в том, что любые объекты смотрятся или увеличенными, или уменьшенными в зависимости от приближения/удаления от дальнего угла к ближнему.

Восприятие кубической комнаты

Если вы смотрите в комнату Амеса через смотровое отверстие (чтобы исключить ненужные точки просмотра), то данная комната кажется нормальной, то есть кубической, но этот образ обманчив. Пол, потолок, стены и дальние окна имеют форму трапеции. Например, дальний левый угол значительно ниже правого переднего. Стены смотрятся перпендикулярными полу, хотя на самом деле они не находятся под прямым углом по отношению к нему.

На схематическом рисунке показаны ощущения смотрящего и данность.

Основная форма - это действительная комната Амеса, пунктирные линии - линии света, форма, нарисованная пунктирно, - это то, какой вы ощущаете саму комнату Амеса. Причем два видимых угла комнаты смотрятся практически равноудаленно от точки просмотра. Но по-настоящему левый видимый угол дальше правого почти в два раза.

Если смотреть в комнату Амеса с другой точки, то ощущение иллюзии исчезнет, то есть комната перестанет быть кубической и откроются все секреты.

Хотя стоит только внимательно присмотреться к представленной фотографии, и элемент трапецеидальности можно найти. Но... На этом и держатся многие современные технологии, а также всевозможные технологии индустрии шоу-бизнеса - стереотипы:).

Практическое применение

Дело в том, что комната Амеса моделируема в современных условиях. Причем сие действие вполне под силу компьютерному дизайнеру. Не тому, кто сидит дома и изучает Photoshop, а тому, чья работа напрямую связана с Blue Box, с так называемой "голубой комнатой", в которой все действующие персонажи снимаются на голубом фоне, после чего оный вырезается и заменяется на компьютерный пейзаж (кстати, есть и Green Box). Так вот, помимо стандартных пейзажей, можно применить и комнату Амеса. Эффект будет превосходен, если создать компьютерное окружение, отталкиваясь от точки просмотра. Хотя это только в теории…

Кристофер М. ИХИХО,
christopher@tut.by

Технологии иллюзий

Итак, продолжим рассматривать "издевательства" над человеческими стереотипами, что мы уже успешно начали делать в "КВ" №46. :)

Square-иллюзии и иррадиация

На самом деле очень многое в технологии иллюзий привнес не этот, а девятнадцатый век. Люди, имеющие на вооружении, в основном, только свою фантазию, сделали фантастические открытия, которые качественно реализовались только в XX веке. Я, например, сломал в себе стереотип того, что XIX век - очень скучный и нединамичный. Как доказательство этому приведу историю иллюзий, основанных на эффекте иррадиации или, как их называют, square-иллюзии.

Иррадиация (от латинского irradio - сияю, испускаю лучи) - термин, используемый в оптике. Известны два типа иррадиации - положительная и отрицательная. Положительная подразумевает увеличение светлых объектов на черном фоне по сравнению с темными объектами тех же размеров на белом фоне. Отрицательная подразумевает обратный эффект при малых яркостях фона.

1856 год. Исследователь Гельмгольтц представил одну из первых иллюстраций, отображающих принципы иррадиации. Из приведенного рисунка можно увидеть, что светлая область смотрится больше темной, но квадраты, находящиеся внутри областей, видятся наоборот.

Иллюзия вьющейся веревки (Twisted Cord Illusion)

В 1894 году исследователь Мунстерберг (Munsterberg) отобразил данную иллюзию в своей популярной коллекции Pseudoptics (обратите внимание на название коллекции, которое по-своему тоже иллюзорно и состоит из двух слов - "pseudo" и "optics"). В 1897-м он повторно опубликовал расчеты этой же иллюзии под названием "Die verschobene Schachbrettfigur" (фигура смещенной шахматной доски).

Все подобные иллюзии называют square-иллюзиями и получаются они за счет использования иррадиации. На рисунке представлена знаменитая работа Мунстерберга, и мы видим, что формы белых прямоугольников, пересеченных черными линиями, кажутся искаженными. То есть, глядя на иллюстрацию, не скажешь, что вертикальные линии - прямые.

Спираль Фрэйзера (Fraser Spiral)

Внимательно посмотрите на два представленных рисунка.

Первый - это и есть Fraser spiral, второй - путь к объяснению реализованного эффекта. Итак, если на первом рисунке мы видим спираль, идущую к центру, то на втором - просто окружности, центр которых совпадает с центром рисунка. На самом деле спираль Фрэйзера - не спираль, а те же окружности, только в них использован иррадиационный эффект, близкий к тому, что мы наблюдали в иллюзии вьющейся веревки. Посмотрите внимательно на второй рисунок, и вы увидите, что каждая окружность состоит из двух: белой (более широкая линия) и черной (более тонкая). В спирали Фрэйзера вместо черных окружностей использованы косые линии, что сообщает общей картине иллюзию вращения. Схему таких линий я приведу на следующем рисунке:

Как видно из схемы, немаловажную роль играют и элементы фона, показанные в виде пересеченных квадратов. На основной картинке - это темные квадраты фона. Косая черная линия идет от одного такого темного квадрата к другому, от внешней стороны белой линии окружности к внутренней. В результате взаимодействия фона, темных и белых линий мы получаем красивый иррадиационный эффект.

Стена кафе (Cafe Wall)

Название иллюзии произошло от действительно существовавшего в девятнадцатом веке (не знаю, существует ли оно сейчас) кафе в городе Бристоль (Великобритания).

Представленная иллюзия отлична от того, что мы могли наблюдать у Мунстерберга. В иллюзии вьющихся веревок были тонкие линии, разделенные широкими темными полосами фона. В иллюзии "стена кафе" "строки" элементов разделены тонкой линией, которая позволяет получить более глубокий эффект путем разделения освещенностей между темными и светлыми элементами.

На приведенной иллюстрации показано несколько вариантов с разными размерами элементов "строк". Причем рисовал последний я сам в стандартном пакете Paint Brush и могу с уверенностью заявить, что все прямоугольники одинаковы по размерам. Каковы ощущения?

Надеюсь, что такие же, как и у меня: средняя линия видится под углом (с правой стороны выше, чем с левой).

Давайте рассмотрим, откуда такой эффект взялся. Все очень просто: как мы уже говорили, светлые объекты на темном фоне видятся большими, а темные - меньшими. И в данном случае величину объектов мы рассматриваем относительно средней линии. Поэтому если в нижней полосе идет чередование темный-белый, в то время, как на верхней находится белый блок, то средняя линия будет "подыматься". Если наоборот, то опускаться. Не верите? Пожалуйста, зеркальное отображение рисунка...

Надеюсь, что на душе похорошело:)

По вашим просьбам: невероятный треугольник (Impossible Triangle)

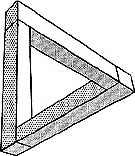
Пришло много писем с просьбами продолжить тему, затронутую в предыдущей статье "Технологии иллюзий", поэтому, я думаю, не написать об этой иллюзии нельзя. Хотя, честно говоря, я не стал бы считать невероятный треугольник иллюзией - скорее, это логическая задача или головоломка. Но, учитывая тот факт, что строгие границы понятию иллюзий провести сложно, остановимся и на нем.

Посмотрите на него внимательно, а теперь представьте, что вы его дадите в качестве чертежа Васе-столяру (поэтому говорю: внимание - ОПАСНО! Прочитали и забыли).

В принципе, невероятный треугольник очень близок по концепции к невероятной лестнице, которую мы рассматривали раньше, хотя последняя представляет собой более сложную конструкцию и смотрится более естественно. Впрочем, спор здесь не уместен, так как люди, участвовавшие в истории появления и продвижения невероятного треугольника, те же, кто "придумал" лестницу.

Итак, 1934 год. Шведский художник Оскар Реутерсворд (Oscar Reutersvard), автор практически всех "невероятных" фигур, впервые представил "невероятный треугольник" в виде рисунка, состоящего из стереометрических фигур - кубов. Получилась объемная фигура, которую можно изобразить, но нельзя реализовать в трехмерном пространстве.

В 1954 году физик Роджер Пенроуз, известный тем, что популяризировал очень много иллюзий и создал большое количество работ, иллюстрирующих уже известные сейчас иллюзии, после посещения лекций датского графика М.К. Эшера воссоздал иллюзию и сделал не менее популярный рисунок. И именно в таком виде многие и представляют "невероятный треугольник", хотя "исходник", как вы понимаете, отличается.

В 1961 году вышеупомянутый художник-график М.К Эшер использовал работу Пенроуза и создал очень популярное произведение "Waterfall" ("Водопад").

На самом деле "невероятных" фигур очень много. Стоит отметить, что работы Оскара Реутерсворда (Oscar Reutersvard) издавались и на русском языке, и информация о других его изобретениях доступна для тех, кто хочет познакомиться с этой темой поближе.

А мы идем дальше.

Кристофер М. ИХИХО,
christopher@tut.by

Технологии иллюзий

Итак, постепенно мы подбираемся к 3D-иллюзиям. Эти иллюзии работают над одним стереотипом мышления человека, выраженного в том, что в любом 2D-изображении человек пытается увидеть объем. Именно об "издевательствах" над этими стереотипами мы и поговорим.

Тени задают траекторию трехмерного движения

Вашему вниманию представлен рисунок с четырьмя шариками. Видно, что они движутся в осях X и Y.

Добавим к этому же рисунку новые элементы - тени, сделанные из однотонно окрашенных овалов разных размеров. Расставим их сообразно предполагаемому движению.

Во-первых, стал явно ощутим эффект движения. И явно прослеживается дуговая траектория полета шарика, появилась третья плоскость. Да, в рисунке есть ошибка. Если мы хотим, чтобы объект удалялся, то он должен уменьшаться. Делаем.

Если убрать из последнего рисунка элементы тени, то эффект движения исчезает, из чего мы можем сделать вывод о том, что гораздо большую роль в эмуляции движения играют тени, нежели изменение геометрических размеров самого тела. Причем два последних рисунка воспринимаются практически одинаково, то есть движение ощущается как в том, так и другом.

Отсюда делаем вывод, что с помощью блока объектов-теней гораздо удобнее и качественнее можно представить само движение. Только в небольшом количестве современных работ, в том числе и анимационных, большое внимание уделяется расстановке теней. При этом тени могут сами влиять на психологическое восприятие геометрических размеров объектов.

На данном рисунке представлены три одинаковых фигуры с различными тенями. Закройте средний шарик пальцем. Два крайних покажутся разными по размерам. Получится эффект типа этого:

"Почему так?" - спросите вы. Представьте, что серый фон - это стена. Свет направлен от нас. Естественно, большая тень будет у объекта, который ближе к нам. По мере приближения объекта к стене тень уменьшается. Тем самым правый объект смотрится более удаленным, а значит - меньшим. К тому же не исключено, что тень, так как она темная, в 2D-пространстве сообщает некий иррадиационный эффект.

Белый, черный и… или просто цвет с различными степенями яркости

Почему компьютерный рабочий стол смотрится объемно? То есть мы явно ощущаем, что нажимаем на кнопки, двигаем слайдеры и так далее. На самом деле мы сталкиваемся ни с чем иным, как с эмуляцией 3D, которая знакома большинству программистов-разработчиков интерфейсов.

Например, когда я программировал в Delphi, пару лет назад в широкой моде были компоненты 3D Label (3D-надписи). Делались они очень просто: брались три одинаковых элемента Label (текст в 2D) и ставились с небольшим смещением относительно друг друга, а потом для каждого в отдельности выбирался свой цвет (см. на рисунок). Из чего после формировался эффект объемности объекта. Кстати, таким же образом можно было рисовать кнопки, выделять фигурные графические элементы. Они могут быть как вдавленными, так и выпуклыми. Не знаю, как эти элементы смотрятся в печатном варианте (поэтому и не привожу их много), но создать собственные 3D-объекты вы сможете сами. Например, попробуйте на сером фоне нарисовать вогнутую вглубь экрана линию. У вас это получится. И, кстати, вы увидите, что для создания одного объемного компонента достаточно трех плоских. Оперируя ими, можно получить нужный нам эффект.

Теперь рассмотрим немного другую тему. Если у вас на рабочем столе установлена стандартная схема Windows, то можно заметить, что в палитре для создания 3D-эффекта используется три цвета: белый, черный и серый. Или же можно "перевернуть" и сказать, что использован серый цвет с различными степенями яркости. Меняем серый на зеленый. Объемная картина сохранится. То есть, мы просто работаем с разными степенями яркости одного и того же цвета. И получаем иллюзию присутствия источника света, обращенного к экрану. И создается эта иллюзия путем "наложения" плоских элементов друг на друга таким образом, чтобы картинка получилась объемной. Почему нельзя нарисовать все тени и объекты сразу? Разделение на плоские объекты более приемлемо, так как таким образом удобнее менять свойства этих объектов. Например, при нажатии на кнопку в программе меняется не картинка, а просто "плоские" объекты, составляющие эту кнопку, меняют свои свойства. Схему применения смены нарисованных элементов можно увидеть во множестве реализаций кнопок в интернет-ресурсах, но это громоздко. И как вы думаете: программистам Quake лучше рисовать каждую стену или же создать ее из компонентов, а потом просто управлять их свойствами? Мы говорим об автоматизации схемы 3D.

Идеальная картина - та, которую мы наблюдаем в природе. Если, например, источник освещает желтую стену, то мы видим огромное количество цветов (от самого яркого желтого до самого темного желтого, если не брать в учет цвет, сообщаемый самим источником). В компьютере это более минимизировано, хотя в современных играх столкнулись с тем, что видео, создававшегося ранее, в основном, для ПО и 2D-игр, не хватает. Поэтому мы и имеем наличие мощных "движков" по поддержке цвета. Огромное внимание уделено оттенкам, теням. Система максимально оптимизирована. Попросту говоря, если на расстоянии трех точек друг от друга находятся белая и черная точки, то эти три точки между ними заполняются различными оттенками серого. И мы говорим о сглаживании цвета, вернее, об эмуляции природного процесса. Поэтому для современных игр рекомендованы видеокарты с максимальными параметрами.

Влияние фона на размеры объектов

Человека очень легко обмануть, уменьшая и увеличивая объекты относительно окружающего пейзажа или даже просто их копируя... В пример приведем самую яркую иллюзию подобного плана, рисунок уже хорошо знакомого нам Роберта Шеппарда.

Кто больше: убегающий или догоняющий? Когда смотришь на рисунок впервые, то, конечно же, удивишься глупости данного вопроса. На самом деле персонажи абсолютно одинаковые - и по форме, и по размеру.

Смотрим на вторую, не менее известную иллюстрацию:

Эти примеры близки к тем, которые мы рассматривали в первой теме данного материала - о способности человека ассоциировать 2D-объекты с 3D. Если в той теме мы оперировали тенями, то в этой - фоном, окружающим объекты. Вторая иллюстрация показывает, как выглядит скопированный объект (человек, идущий сзади), по сравнению с тем, каким он должен выглядеть на самом деле на переднем плане (человек, идущий впереди). Естественно, если убрать впереди идущего, то мы получим картину, схожую с рисунком Шеппарда, и результат эффекта - скопированная фигура уменьшилась в размерах.

Кристофер,
christopher@tut.by

Треугольник Паскаля

Есть в форме треугольника что-то тайное, глубоко символическое. Недаром треугольная форма была выбрана древними египтянами в качестве символа вечности и воплощена в пирамидах. Ту же форму имеет и загадочный масонский символ, изображенный Николаем Рерихом на обратной стороне однодолларовой купюры (это та самая пирамида с тринадцатью ступенями и всевидящим оком на вершине²). В математике такой глубоко символичной пирамидой является знаменитый треугольник Паскаля. Треугольник Паскаля обладает целым рядом замечательных свойств. О нем написано множество статей и книг. С появлением вычислительных машин построение треугольника Паскаля стало излюбленной задачкой для начинающих при изучении основ программирования. Элементами этой арифметической структуры являются так называемые биномиальные коэффициенты. Комбинаторный смысл биномиальных коэффициентов состоит в том, что они представляют собой количества различных k-членных комбинаций из n-элементного множества без повторений. То есть треугольник Паскаля состоит из чисел, каждое из которых есть количество способов выбрать k шариков из мешка, в котором таких шариков n штук (k < или = n). При этом в треугольнике n - это номер строки, а k - номер элемента в строке (и в том, и в другом случае нумерация начинается с нуля). Есть формула, которая позволяет вычислить любой биномиальный коэффициент непосредственно, зная k и n. Но в этой прямой формуле присутствуют факториалы, которые очень быстро переполняют объемы ячеек вычислительной машины с ростом значений k и n. Поэтому для построения треугольника Паскаля воспользуемся одним замечательным его свойством, состоящим в том, что любой из элементов представляет собой сумму двух его верхних соседей. В этом случае умножение заменяется простым сложением. Строго говоря, таким способом нельзя вычислить крайние единички, поскольку над ними нет двух соседей, но при написании программы можно зарезервировать в массиве виртуальные нули и тем самым сохранить универсальность общего правила.

Private Sub Form_Click()
Dim a(16, 16) As Long
n = 15
s = 800
a(1, 0) = 1
For j = 1 To n
 CurrentX = (Width / 2) - j * 0.5 * s
 For i = 1 To j
  x = CurrentX
  a(i, j) = a(i - 1, j - 1) + a(i, j - 1)
  If a(i, j) Mod 2 = 1 Then
   ForeColor = RGB(0, 0, 0)
  Else
   ForeColor = RGB(255, 0, 0)
  End If
  Print a(i, j);
  CurrentX = x + s
 Next i
 Print
 Print
Next j
End Sub

В приведенном фрагменте кода нечетные элементы треугольника Паскаля окрашиваются в черный цвет, а четные - в красный. Если продолжить такие "разноцветные" вычисления для более высоких значений k и n, то можно наблюдать занятное и, опять-таки, глубоко символичное явление, как сквозь растущие значения биномиальных коэффициентов начинают все явственнее проступать фрактальные геометрические структуры Серпинского.

А. КОЛЕСНИКОВ,
andr61@mail.ru