
|
|
|
|
|
|
|
|
|
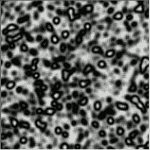
Искусственная жизнь клеточных автоматовНаблюдая за любыми проявлениями жизни, легко заметить нечто такое, что отличает их от неживых объектов. В чем же разница? Почему поведение живого так разительно внешне отличается от всякого иного механического движения в неживой природе? Раскрыть или, по крайней мере, пролить свет на общие принципы, управляющие поведением живых объектов, удалось английскому математику Дж. Конвэю. Он придумал очень простую игру, которую так и назвал - "Жизнь". Напомним, что суть дела заключается в следующем. На бесконечном клеточном поле обитает популяция фишек. Каждая клеточка поля может быть либо заселена фишкой, либо пуста. Моменты времени в игре сменяют друг друга дискретно - 1, 2, 3... В пустой клетке рождается новая фишка, если в предыдущий момент времени в окрестных восьми клетках обитало ровно три живых ее собрата. Фишка, вокруг которой обитало меньше двух или больше трех фишек, в следующий момент времени умирает, а занятая ею клетка освобождается. Если изначально разбросать на клеточном поле некоторое количество фишек, а затем дать возможность исходной популяции развиваться по описанным простым правилам, то можно будет наблюдать те особые процессы характерного "копошения", свойственные только живым системам. Именно поэтому игра и получила свое название - "Жизнь". Сразу с момента своего возникновения "Жизнь" завоевала бешеную популярность во всем мире. Множество программистов разрабатывало свои оригинальные версии игры. Стали выпускаться даже специализированные журналы. В чем же секрет столь громкой популярности и такого разительного сходства поведения популяции фишек с поведением реальных колоний неких живых единиц? Возможно, разгадка кроется в том, что в игре "Жизнь" воспроизводится характерный для живых систем принцип отношений между частью и целым. Все части живых систем активны, они одновременно влияют друг на друга, поэтому всякое живое образование находится в постоянном сложном движении, в которое вовлечены сразу все его элементы. Локальная населенность окрестности каждой отдельной клетки определяет судьбу данной ячейки поля в следующий момент дискретного времени. Причем правила взаимодействия клеток подобраны так, что не поощряется ни перенаселение, ни чрезмерная пустынность клеточного поля. В результате на экране смена поколений фишек сливается в причудливый танец, который постепенно либо замирает, либо переходит в регулярные пульсации. В игре "Жизнь" каждая из клеток может находиться лишь в одном из двух возможных дискретных состояний. А что если попытаться придумать игру, в которой каждая из клеток могла бы принимать не два значения (ноль и единица), а вмещала бы любое действительное число между ними (то есть, например, могла быть заселенной на 0.81 или на 0.38). Пусть имеется некая клеточная поверхность. Состояние каждой из клеток этой поверхности характеризуется действительным числом "x", находящимся в интервале от 0 до 1. Число "x" можно интерпретировать как степень заселенности клетки. Тогда клетка, содержащая значение 0, пуста; клетка, содержащая значение 0.2, заполнена на 20% и т. д. Затем предположим, что в следующий момент времени, которое изменяется в игре дискретными тактами, степень заселенности клетки определяется состоянием ее ближайшей окрестности, т.е. средней заселенностью соседних восьми клеток. Среднюю заселенность окрестности будем определять как деленную на 8 сумму заселенностей соседних восьми ячеек. Предположим, что наиболее оптимальные условия для клетки создаются, когда средняя заселенность ее окрестности находится примерно на уровне 0.5. Тогда ячейке не слишком тесно и не слишком одиноко. Математически это может быть выражено следующей формулой: Xk+1=4xYkx(1-Yk), где Xk+1 - заселенность некоторой клетки в k+1 момент времени, Yk - средняя заселенность окрестности данной клетки в k-тый момент времени. График зависимости заселенности клетки в следующий момент времени от средней заселенности ее окрестности в текущий момент времени будет иметь вид параболы с вершиной в точке с координатами (0.5, 1). То есть, наиболее комфортные условия для клетки создаются, когда ее окрестность в момент времени k заселена в среднем наполовину. Для того, чтобы не ломать себе голову над тем, как трансформировать правила игры и алгоритмы расчетов на границах игрового поля (т.к. смоделировать бесконечное клеточное поле на компьютере с пусть даже очень большой, но все же ограниченной памятью не представляется возможным), целесообразно свернуть его в тор (тором математики называют фигуру в форме бублика). Тогда клеточная поверхность не будет иметь краев, но будет ограничена по площади. Для этого двумерные массивы, в которых будут сохраняться предыдущая и последующая конфигурации, необходимо описать (во все стороны) на единичку больше, чем выбранный размер игрового поля, оставив тем самым поля для "склейки". Если Вы выбрали размер игрового поля (1..200, 1..200), то массивы следует описать так: Dim x (0 to 201, 0 to 201) As Single Dim y (0 to 201, 0 to 201) As Single Затем для "сворачивания" клеточного поля, которое следует производить перед расчетом конфигурации каждого очередного поколения, значения крайних клеток необходимо скопировать в поля для "склейки". x(0, 0) = x(n, n): x(0, n + 1) = x(n, 1) x(n + 1, 0) = x(1, n): x(n + 1, n + 1) = x(1, 1) For k = 1 To n x(0, k) = x(n, k): x(k, 0) = x(k, n) x(n + 1, k) = x(1, k): x(k, n + 1) = x(k, 1) Next k Для расчета следующей конфигурации ячеек на игровом поле можно использовать вложенный цикл: For i = 1 To n For j = 1 To n s = x(i + 1, j) + x(i, j + 1) + x(i, j - 1) + x(i + 1, j + 1)+ x(i + 1, j - 1) + x(i - 1, j) + x(i - 1, j + 1) + x(i - 1, j - 1) s = s / 8 y(i, j) = 4 * s * (1 - s) c = 255 * (1 - y(i, j)) Screen.Pset (i, j), RGB(c, c, c) Next j Next i Для успешного округления переменной "с" необходимо, чтобы она была описана как переменная типа BYTE. Перед расчетом конфигурации следующего поколения нужно обновить значения всех элементов массива "x", заменив их вновь рассчитанными значениями (массив "y"). Пусть изначально заселенность каждой клетки представляет собой результат случайного равновероятного выбора произвольного числа из интервала от 0 до 1 (X(i,j)= rnd), а в дальнейшем в действие вступают описанные правила. Через некоторое время можно будет наблюдать, как на основе микроскопических межклеточных взаимодействий в процессе эволюции исходной хаотической конфигурации формируются макроскопические структуры заселенности клеточного поля. Несмотря на то, что закон взаимодействия клеток на микроскопическом уровне крайне прост и строго детерминирован, макроскопическая эволюция системы выглядит крайне сложно. В процессе эволюции на клеточном поле формируются изменчивые замысловатые кольцевые структуры, в которых чередуются зоны с высокой и низкой заселенностью.
Эти картины сильно напоминают некие микробные колонии. Виртуальные микробы копошатся, растекаются, делятся, одним словом - живут. Возможно, описанную игру следовало бы назвать "Хаос", поскольку то, что происходит на экране, пожалуй, точнее всего можно определить именно как хаос. Причем речь идет не о скучном статистическом хаосе пустого рябящего телевизионного экрана, а о хаосе в космогоническом античном смысле - о хаосе первородного кипения формотворящих сил, которые в конечном счете и породили то, что называется "Жизнь". А.КОЛЕСНИКОВ,
Клеточные автоматы и компьютерная экология
Кто-то точно подметил, что разговор о погоде становится интересным лишь при первых признаках конца света. Сегодня ученые и политики обсуждают проблемы погоды на глобальных форумах, да и простые люди начинают потихоньку интересоваться погодой, причем не только на ближайшие выходные, но и вообще… Атмосфера - огромная, сложнейшая, распределенная, динамическая система. Предсказывать ее поведение чрезвычайно трудно, часто просто невозможно. Глядя на висящие в небесной синеве замысловатые облачные структуры, мы не всегда задумываемся о том, насколько масштабные и драматические процессы происходят там, в вышине. Совсем иное впечатление оставляет ускоренная съемка облачного неба. Картинка эволюции роящихся облачных масс невольно наводит на размышления о природе времени и смысле земного существования. Схожие, но более тревожные мысли навевают кадры, изображающие расползание смога над крупными мегаполисами или, хуже того, постепенной диффузии ядерного гриба… Все мы помним старые черно-белые учебные фильмы, повествующие о формировании зон заражения после атомного взрыва. Они классифицируются по степени опасности. Вблизи эпицентра располагается "мертвая" зона сплошного интенсивного заражения. Далее, в зависимости от направления ветра, зоны распределяются в виде вложенных друг в друга эллипсоидов рассеивания. В принципе, схожей будет картина распространения и любого другого загрязнителя от точечного источника, например, от дымящей трубы, взорвавшегося реактора или апокалиптической звезды из библейского пророчества. Процесс распространения загрязнителя в атмосфере - это процесс рассеивания и смешивания его частиц с частицами воздуха. На ход этого процесса существенное влияние оказывают собственные движения воздушных масс, то есть ветра. В одной и той же местности они дуют в различных направлениях с определенной частотой. Данные о частотах ветров наносятся на особую диаграмму, имеющую романтическое название, воспетое во множестве бардовских песен, - роза ветров. Частицы загрязнителя попадают от первоначального источника в соседние области. Затем из областей, непосредственно примыкающих к источнику, распространяются уже в их окрестностях, и так далее. Сам характер этого процесса указывает на то, что для моделирования рассеивания загрязнителя в атмосфере можно использовать подход, основанный на идеологии клеточных автоматов. В этом случае исследуемый участок представляется в виде клеточного поля. На поле помечаются клетки, в которых находятся эпицентры распространения загрязнения или заражения. Затем концентрацию загрязнителя в каждой клетке поля можно, например, приближенно оценивать по формуле:
где ak - это массив из девяти элементов, содержащий вероятности ветров соответствующих восьми направлений и вероятность штиля. Само собой разумеется, что девять вероятностей ветров различных направлений, включая вероятность штиля, должны в сумме давать единицу. C*k - это вектор из девяти элементов, содержащий концентрации загрязнителя в соседних с данной восьми клетках и в ней самой. Шаг за шагом для всех клеток поля вычисляется сумма произведений концентраций в соседних восьми ячейках на соответствующие вероятности ветров. К сумме прибавляется еще и произведение вероятности штиля на концентрацию загрязнителя в самой текущей клеточке. Для нормальной работы программы необходимо иметь две копии клеточного поля. В одной из копий следует хранить предыдущее поколение, а в другой - последующее. При смене поколений содержимое последующего поколения становится предыдущим. Из расчетов исключаются крайние ряды ячеек. Это делается для того, чтобы избежать "пограничных" проблем при применении формулы (1). Повторяя расчеты многократно, мы можем наблюдать динамику формирования эллипсоидов рассеивания во времени. При разовом "впрыске" загрязнителя в какую-либо ячейку он быстро рассасывается по клеточному массиву. Для получения более выразительной картины рассеивания в предлагаемом на врезке фрагменте программного кода "впрыск" загрязнителя в соответствующие ячейки осуществляется в начале расчета каждого очередного поколения. Значения концентраций выбросов вводятся в ячейки в неких произвольных единицах. Для восприятия результатов моделирования
важна раскраска клеток. В приведенном
программном фрагменте использован алгоритм,
переводящий значения концентраций загрязнителя
в различные градации яркости цветов - от
темно-красного до темно-зеленого. А.КОЛЕСНИКОВ, DefByte I-K
DefInt L-N
Dim G As Byte
Dim a(1 To 9) As Single
Dim b(1 To 200, 1 To 200) As Single
Dim c(1 To 200, 1 To 200) As Single
Dim Color As Long
Dim Zmin As Single
Dim Zmax As Single
Dim R As Single
Dim R4 As Single
Dim Z14 As Single
Dim Z24 As Single
Dim Z34 As Single
Private Sub Form_Click()
a(1) = 0.05
a(2) = 0.05
a(3) = 0.1
a(4) = 0.1
a(5) = 0.1
a(6) = 0.1
a(7) = 0.1
a(8) = 0.15
a(9) = 0.25
z = 7
Zmin = 0
Zmax = 2
R = Zmax - Zmin
R4 = R / 4
Z14 = Zmin + R4
Z24 = Z14 + R4
Z34 = Z24 + R4
n = 50
G = 50
For f = 1 To G
b(35, 35) = z
b(45, 15) = z / 2
For i = 2 To n - 1
For j = 2 To n - 1
c(i, j) = 0
k = 0
For l = -1 To 1
For m = -1 To 1
k = k + 1
c(i, j) = c(i, j) + a(k) * b(i + l, j + m)
Next m
Next l
Next j
Next i
For i = 1 To n
For j = 1 To n
Color = SetColor(c(i, j))
Line (6 * (i - 1), 6 * (j - 1))-(6 * i - 1, 6 * j - 1), Color, BF
b(i, j) = c(i, j)
Next j
Next i
Next f
End Sub
Public Function SetColor(z As Single) As Long
Dim t As Byte
Select Case z
Case Is < Zmin
SetColor = RGB(0, 63, 0)
Case Zmin To Z14
t = 63 + 192 * (z - Zmin) / R4
SetColor = RGB(0, t, 0)
Case Z14 To Z24
t = 255 * (z - Z14) / R4
SetColor = RGB(t, 255, 0)
Case Z24 To Z34
t = 255 * (1 - (z - Z24) / R4)
SetColor = RGB(255, t, 0)
Case Z34 To Zmax
t = 63 + 192 * (1 - (z - Z34) / R4)
SetColor = RGB(t, 0, 0)
Case Is > Zmax
SetColor = RGB(63, 0, 0)
End Select
End Function
Химия и жизнь клеточных автоматов"Чтобы приготовить эликсир мудрецов, или философский камень, возьми, сын мой, философской ртути и накаливай, пока она не превратится в зеленого льва. После этого прокаливай сильнее, и она превратится в красного льва... Киммерийские тени покроют реторту своим темным покрывалом, и ты найдешь внутри нее истинного дракона, потому что он пожирает свой хвост... Он загорится и, приняв вскоре великолепный лимонный цвет, вновь воспроизведет зеленого льва... Наконец, мой сын, тщательно ректифицируй, и ты увидишь появление горючей воды и человеческой крови" (цит. по Рабинович В.Л. Алхимический миф и химера собора Парижской богоматери//в книге Заблуждающийся разум?: Многообразие вненаучного знания/Отв. ред. и сост. И.Т. Касавин.-М.: Политиздат, 1990.-464 с., стр. 100) Примерно так представляли себе средневековые алхимики процесс приготовления философского камня - средства для превращения или "трансмутации" металлов в золото. Кроме философского камня, у алхимиков был еще один знаменитый проект - создание химическим путем искусственного человечка - гомункулуса. Своих целей они так и не добились, хотя существенно обогатили арсенал технических средств, заложив тем самым фундамент современной экспериментальной химии. К таинствам превращения веществ в живых системах наука подобралась только в XX столетии. Причем даже современная биохимия пока не может в полной мере искусственно воссоздавать процессы, лежащие в основе феномена жизни. Тем не менее, определенные успехи в области моделирования необыкновенных "жизнеподобных" химических реакций в современной науке все же достигнуты. Огромный шаг в этом направлении совершил сразу после войны советский ученый Белоусов. История его открытия весьма драматична. Работы Белоусова долго отказывались признавать. Слава пришла к ученому уже после смерти. Открытая реакция была названа его именем и вошла во все классические труды по неравновесной термодинамике и теории самоорганизации. Причина длительного непризнания открытия состояла в том, что оно не вписывалось в догмы традиционной термодинамики. В этом смысле реакция Белоусова представляет собой глубокую и общую метафору биохимических процессов. Химию живых систем невозможно понять в рамках традиционной термодинамики. Химические процессы в живых системах идут в совсем ином направлении, чем указывает классическая физическая химия, а именно - в сторону роста упорядоченности и усложнения итоговых структур. Из химического хаоса возникает химический порядок. В процессе реакции, открытой Белоусовым, из первичного хаоса смеси реагентов рождаются макроскопические упорядоченные структуры в форме кольцевых волн. Это, конечно, пока еще не гомункулус, но существенный шаг вперед по пути моделирования химических процессов нового типа - самоорганизационных процессов. А именно они и лежат в основе возникновения и эволюции живых систем. В еще большей степени проблема создания гомункулуса, т.е. некоего подобия искусственного существа, нашла свое выражение в компьютерных науках. На заре компьютерной революции, так же, как и в эпоху расцвета алхимических исканий, казалось, что нужно еще немного наворотить электроники, чуть-чуть подработать программное обеспечение и… электронный гомункулус начнет вещать бесстрастным металлическим голосом из чрева железных шкафов, набитых проводами и обрамленных мигающими лампочками. По своей наивности эти мечты были вполне сравнимы с фантазиями алхимиков, только-только начавших постигать таинства химических превращений веществ. Им так же, как и пионерам компьютерной эры, представлялось, что их новая всемогущая наука наук перевернет все человеческие знания, позволит варить золото из ртути и, смешивая химические ингредиенты, взращивать в ретортах искусственных человечков. Несмотря на всю наивность и беспочвенность этих мечтаний, те и другие, несомненно, продвигали познание вперед, и, кто знает, может, когда-нибудь мечта человечества об искусственном создании чего-то, хотя бы отдаленно напоминающего живые системы, все-таки сбудется. Ниже мы рассмотрим одну игру, принадлежащую к семейству игр клеточных автоматов, в которой удивительным образом соединились химия, компьютерные науки и современная теория самоорганизации. Речь пойдет о так называемой перемешивающей машине. Перемешивающая машина - это своеобразное развитие знаменитой клеточной модели жизни Дж. Конвэя. Как и все клеточные автоматы, перемешивающая машина представляет собой матрицу, состоящую из множества параллельно взаимодействующих друг с другом ячеек. Именно таким образом организованные параллельные вычислительные устройства, по мнению многих теоретиков искусственного интеллекта, позволят приблизиться к решению проблемы моделирования настоящих мыслительных процессов. Правила взаимодействия ячеек в перемешивающей машине таковы, что дают возможность моделировать волновые структуры, точь в точь напоминающие те, которые можно наблюдать в уже упоминавшейся химической реакции, открытой Белоусовым. Клеточный автомат "Перемешивающая машина" был предложен М. Герхардом и Х. Шустером из Билефельдского университета ФРГ (см. статью А.К. Дьюдни "Перемешивающая машина"-клеточный автомат, моделирующий химические реакции//В мире науки, 1988 - №10, с.82-86). Правила взаимодействия ячеек автомата Герхарда и Шустера удобно излагать, используя эпидемическую терминологию. Отдельная клетка может находиться в некотором множестве состояний. Обозначим их целыми числами от 0 до n. Клетки, находящиеся в состоянии 0, будем называть здоровыми, а клетки, находящиеся в состоянии n, - больными. Все остальные промежуточные состояния интерпретируются как зараженность различной степени. Иными словами, клетка в рассматриваемой модели может быть либо здорова, либо заражена, либо больна. В зависимости от того, к какому из этих трех типов клетка относится в данный момент времени t, ее судьба в момент времени t+1 складывается по-разному. Если клетка здорова (то есть ее состояние x(i,j)=0), то ее состояние в момент времени t+1 будет определяться формулой: Y(i,j)=Round(A/k1,0)+Round(B/k2,0), Здесь A - это количество зараженных, а B - количество больных клеток в окрестности. Константы k1 и k2 представляют собой некие изначально задаваемые управляющие параметры. Функция Round возвращает округленное до указанного количества знаков значение выражения. Если в момент времени t клетка заражена (то есть x(i,j) имеет любое значение, большее 0, но меньшее n), то в момент времени t+1 ее состояние будет определяться формулой: Y(i,j)=Round(S/A,0)+G, Здесь, как и прежде, А - количество зараженных соседей в окрестности клетки, а S - это сумма состояний всех соседних клеток, включая саму X(i,j). Константа G также представляет собой некий изначально задаваемый управляющий параметр. Следует помнить, что Y(i,j) ни при каких условиях не может превышать максимального значения n. Поэтому, если в процессе вычислений значение выходит за эти рамки, его следует приравнять к n. Наконец, если клетка в момент времени t больна (то есть, ее состояние равно n), то в следующий момент времени t+1 она всегда переходит в состояние 0, то есть выздоравливает. Программный код, моделирующий поведение перемешивающей машины, приведен на врезке. Для того, чтобы не изменять общие правила на границах поля, я "свернул" клеточную матрицу в тор. Процедура сворачивания лишает поверхность ее границ, а значит, и "пограничных" проблем. Для хранения состояний ячеек в предыдущем и последующем поколении используются два двухмерных массива - X(i,j) и Y(i,j). Результат выводится на форму в виде мозаики квадратиков, раскрашенных в градации серого цвета в соответствии с состояниями ячеек в момент времени t. При моделировании перемешивающей машины я категорически рекомендую читателям использовать анимационные технологии, поскольку динамика образования и движения волновых фронтов производит совершенно неповторимое впечатление именно в движении. Как и во многих других играх клеточных автоматов, в поведении перемешивающей машины угадываются биоподобные черты. Клеточная плазма, первоначально хаотическая, начинает беспокойно пульсировать. Постепенно ее пульсации становятся все более регулярными и, наконец, в ее недрах рождаются устойчивые центры, генерирующие медленно распространяющиеся во все стороны ряды кольцевых волн. Наверное, нечто подобное происходит в коре нашего головного мозга, когда из хаоса нахлынувших на него нервных импульсов (например, во время чтения этой статьи) постепенно рождаются устойчивые мыслительные волны и происходит осознание поступающей в мозг информации. В описанной игре воспроизводится удивительное явление самоорганизации, которому, по существу, обязан своим существованием и окружающий нас мир, и мы сами. Из хаотической смеси находящихся в случайных состояниях клеточек постепенно сами собой возникают некие макроскопические образования. Массивы клеток согласованно циклически меняют свои состояния, кооперируясь в связные коллективные структуры. Не правда ли, картина, достойная быть первым кадром научно-популярного фильма под названием "Сотворение мира". Если когда-либо в будущем удастся создать машины, способные действительно думать, а не просто считать, то они, несомненно, будут основываться на принципах самоорганизации. В первой главе известной монографии семидесятых годов "Искусственный интеллект", ее автор Э. Хант писал: "Можно ли сказать что-нибудь содержательное о самоорганизации самой по себе? Некоторые думают, что можно, но я не из их числа… Это предубеждение и послужило причиной того, что самоорганизующиеся системы в книге не обсуждаются". Сейчас феномен самоорганизации стал намного более понятен современной науке. И именно в этом направлении следует искать решение проблемы искусственного моделирования мышления. С древнейших времен лучшие умы человечества пытаются постичь тайну развития. Как, почему хаотическая первосубстанция, самоструктурируясь, породила и продолжает порождать столь сложные и высокоупорядоченные структуры? Уже очень давно было замечено, что основа механизма саморазвития материи состоит в вечном стремлении различных противоначал слиться в недостижимой гармонии. В играх клеточных автоматов эта диалектика предстает в овеществленном, наблюдаемом виде, демонстрируя феномен развития в очень ярких и завораживающе красивых формах. А. КОЛЕСНИКОВ, Dim x(210, 210) As Integer Dim y(210, 210) As Integer Dim c As Byte Dim n As Byte Dim m As Byte Dim k1 As Single Dim k2 As Single Dim g As Byte Private Sub Form_Click()
For f = 1 To 150
x(0, 0) = x(n, n): x(0, n + 1) = x(n, 1): x(n + 1, 0) = x(1, n): x(n + 1, n + 1) = x(1, 1)
For k = 1 To n
x(0, k) = x(n, k): x(k, 0) = x(k, n): x(n + 1, k) = x(1, k): x(k, n + 1) = x(k, 1)
Next k
For i = 1 To n
For j = 1 To n
Select Case x(i, j)
Case Is = 0
a = 0: b = 0
For k = i - 1 To i + 1
For l = j - 1 To j + 1
Select Case x(k, l)
Case 1 To m - 1
a = a + 1
Case Is = m
b = b + 1
End Select
Next l
Next k
y(i, j) = Round((a / k1), 0) + Round((b / k2), 0)
blue = 0: red = 0: green = 0
Case 1 To m - 1
a = 0: s = 0
For k = i - 1 To i + 1
For l = j - 1 To j + 1
If x(k, l) > 0 And x(k, l) < m Then a = a + 1
s = s + x(k, l)
Next l
Next k
y(i, j) = Round((s / a), 0) + g
If y(i, j) > m Then y(i, j) = m
Case Is = m
y(i, j) = 0
End Select
c = (x(i, j) / m) * 255
Line (4 * (i - 1), 4 * (j - 1))-(4 * i - 1, 4 * j - 1), RGB(c, c, c), BF
Next j
Next i
For i = 1 To n
For j = 1 To n
x(i, j) = y(i, j)
Next j
Next i
Next f
End Sub
Private Sub Form_Load() Randomize n = 25 m = 100 k1 = 5 k2 = 4 g = 28 For i = 1 To n For j = 1 To n x(i, j) = m * Rnd Next j Next i End Sub
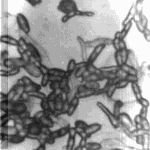
Эволюция клеточных симметроидов
Клеточные автоматы представляют собой одно из самых красивых и удивительных открытий в области компьютерной математики. Клеточная плазма ведет себя как живая. Она кипит, пульсирует, рождает и вновь поглощает разнообразные диковинные структуры. Клеточные автоматы, пожалуй, самая яркая модель того, что в философии называют диалектическим самодвижением. В каком-то смысле можно утверждать, что игры клеточных автоматов воспроизводят наиболее существенные свойства эволюционирующей материи. Диалектические идеи философов древности в них предстают в своем овеществленном виде. Самоорганизационные процессы, которые происходят в недрах искусственной клеточной плазмы, представляют собой одно из ярчайших доказательств справедливости диалектической модели саморазвития материи. На играх клеточных автоматов можно наглядно проиллюстрировать те принципы, на основе которых из первородного хаоса вселенной рождались упорядоченные структуры нашего мира. Разумеется, речь идет лишь о принципиальной аналогии, но аналогии столь эвристичной и убедительной, что мы без труда узнаем на экране дисплея интуитивно ощущаемые нашим сознанием характерные черты великого формотворящего процесса эволюции материи. Клеточная плазма напоминает некую особую креативную жидкость, которая, переливаясь и перелепливаясь, может принимать различные изменчивые формы. Опять, как и в случае комплексных фрактальных множеств, вспоминается живой океан Соляриса, порожденный фантазией Станислава Лема. Наверное, не случайно многие математические объекты, открываемые в области синергетики (единственной строгой научной дисциплины, прикоснувшейся к проблеме развития) так похожи на описания структур, рождаемых его живым, эволюционирующим океаном. Клеточная плазма состоит из отдельных ячеек, каждая из которых соседствует с восемью примыкающими к ней клетками. Состояние каждой отдельной клетки определяется состоянием ее непосредственных соседей. Если начать моделирование с хаотической конфигурации клеток, предварительно случайно разбросав их по всей поверхности, то можно наблюдать, как исходный хаос будет постепенно трансформироваться. В зависимости от принятых правил игры, клеточная "жидкость" может постепенно образовывать "затвердевающие" сгустки, расходящиеся кольцевые волны или погрузиться в состояние изменчивого динамического хаоса. Все эти эволюции напоминают "копошение" некой протобиологической субстанции, готовой породить в своих недрах зачатки будущей жизни. Индивидуальное развитие живого организма называется в биологии онтогенезом. Онтогенез представляет собой, наверное, одно из наиболее поразительных и загадочных явлений в природе. Как, почему, откуда возникает строгий и сложнейший порядок биологических структур? Теория естественного отбора не может объяснить этот феномен. Дарвиновский принцип выживания наиболее приспособленных объясняет лишь, почему биологические организмы устроены целесообразно, но ничего не говорит о том, каковы механизмы образования сложнейших, высокоупорядоченных биологических "машин" и их индивидуальной эволюции. Что управляет онтогенезом? Какие невидимые воздействия формируют живые тела? На первый взгляд кажется невероятным, чтобы столь сложные структурные образования формировались сами собой, без вмешательства неких внешних организующих сил. Именно из этого предположения исходит популярная до сих пор теория номогенеза, которая постулирует наличие в природе неких неизвестных внешних управляющих воздействий. При этом вопрос о происхождении этих воздействий остается открытым. Номогенетическая точка зрения не является, однако, удовлетворительным научным объяснением явления онтогенеза. Во-первых, эта гипотеза нарушает один из основополагающих методологических императивов научного метода: не умножай сущностей более необходимого. Не следует искать каких-то экзотических внешних причин, в то время когда эти причины могут быть непосредственно связаны с внутренней природой самого исследуемого объекта. Во-вторых, из всего опыта развития науки можно заключить, что алгоритмы, по которым протекают даже самые сложные природные явления, не содержат излишних причин. Природа всегда обходится самыми простыми, но подчас гениальными механизмами. Ученый и философ XIX - нач. XX века Эрнст Геккель, помимо ряда фундаментальных научных и философских трудов, создал замечательный живописный атлас, который назвал - "Красота форм в природе". Атлас содержит множество удивительно красивых изображений самых различных организмов, начиная от простейших живых форм и заканчивая высшими животными. Иллюстрации Геккеля заставляют обратить внимание на то, сколь строгий математический порядок царит в живой природе, сколь сложна и в то же время строго закономерна структура биологических объектов. Если никто и ничто не управляет их развитием, то порядок биологических структур каким-то образом должен возникать сам собой из взаимоотношений самих делящихся клеток. В одной из своих недавних статей Иван Жилин сообщил читателям "КВ" о полной расшифровке американскими учеными генома плодовой мушки - дрозофилы. Из тех шестидесяти мегабайт далеко не все гены кодируют белки. Кроме "белковых" генов и "молчащей", "эгоистичной" ДНК, в геномах живых организмов есть так называемые регуляторные гены. В их функцию входит включение или выключение других генов, в зависимости от действия тех или иных внешних факторов. Фон внешних факторов для каждой клеточки многоклеточного организма создают соседние клетки и внешняя среда. Клетки тела многоклеточного организма способны сложным образом управлять друг другом, переключая друг другу те или иные регуляторные гены. Развивающийся многоклеточный организм можно представить как очень большой и сложный трехмерный клеточный автомат. В играх клеточных автоматов действуют те же принципы взаимного управления элементов системы друг другом, а локальная корреляция событий в соседних ячейках нередко порождает весьма сложные и упорядоченные структуры, форма которых определяется правилами взаимодействия ячеек между собой. В природе действует общий принцип, согласно которому сложные структуры возникают там, где управляющие параметры принимают пограничные, критические значения. Например, биологическая эволюция протекает именно на Земле, а не на Меркурии, Венере или Марсе. Земля находится как раз в пограничной температурной зоне - не слишком далеко, но и не слишком близко от Солнца. На Земле существуют такие условия, при которых молекулы движутся достаточно "энергично" для того, чтобы могли интенсивно протекать формообразовательные физико-химические процессы, и в то же время их энергия не является чрезмерной, разрушительной для сложных биохимических структур. Земная жизнь развивается в тонком пограничном слое, отделяющем испепеляющий жар солнца от ледяного космического холода. Идея клеточного автомата, о котором пойдет речь ниже, возникла именно под влиянием выше изложенных философских соображений. В одном из прошлых номеров "КВ" я уже описывал правила взаимодействия ячеек этого автомата (см. "КВ" №26, 8-14 июля 1999 г.). Напомню, что их суть сводится к следующему. Пусть состояние каждой отдельной клеточки характеризуется неким вещественным параметром x, который может принимать любые значения в интервале между 0 и 1. В очередной следующий момент времени состояние клетки определяется средним значением Z, вычисленным по сумме значений параметра в соседних восьми клетках. Состояние каждой ячейки в следующий момент времени вычисляется по формуле X=4xZx(1-Z). В указанной выше статье описывался вычислительный эксперимент, в котором в начальный момент времени все клетки игрового поля заполнялись случайными числами, равномерно распределенными в интервале от 0 до 1. Далее компьютерная программа моделировала эволюцию исходной хаотической конфигурации на всем клеточном поле. Теперь проделаем иной вычислительный эксперимент. Первоначально в центре пустого поля выберем единственную клетку. Запишем в нее случайное число. Этот фрагмент программы может выглядеть следующим образом. l = 200: m = 1 Randomize: x(l, l) = Rnd Screen.Cls Здесь l - индекс исходной клетки в двумерном массиве x (общий размер массива x в приведенном примере составлял 400x400 элементов), а m - счетчик поколений. Затем запустим в действие описанные правила. В процессе моделирования будем наблюдать за развитием клеточной популяции, берущей начало от одной единственной исходной клетки. При написании моделирующей программы следует учесть, что ненулевые значения могут возникать лишь в ячейках, непосредственно примыкающих к уже заполненным клеткам. На первом шаге игры заполнятся лишь восемь соседних с исходной клеткой ячеек. На втором шаге игровое поле расширится еще на один ряд клеток с каждой стороны, и так далее... Поэтому моделирующая программа должна постепенно расширять анализируемое игровое поле от исходной клетки в каждую сторону на один ряд с каждой стороны. k = l - m: n = l + m For i = k To n For j = k To n s = x(i + 1, j) + x(i, j + 1) + x(i, j - 1) + x(i + 1, j + 1) + x(i + 1, j - 1) + x(i - 1, j) + x(i - 1, j + 1) + x(i - 1, j - 1) s = s / 8 y(i, j) = 4 * s * (1 - s) c = 255 * (1 - y(i, j)) Screen.Pset (i, j), RGB(c, c, c) Next j Next i Вычислительный процесс должен продолжаться до тех пор, пока растущая клеточная конфигурация не достигнет границы игрового поля. В природе развитие эмбриона живого организма
начинается также с одной оплодотворенной клетки.
Исходная клетка делится и вскоре образуется
полая сфера с однослойной клеточной оболочкой,
называемая бластулой. Затем бластула выгибается,
образуя так называемую гаструлу. Далее в
процессе онтогенеза структура эмбриона,
причудливым образом складываясь, продолжает
усложняться от фазы к фазе. Между процессом
индивидуального развития многоклеточных
организмов и описанным вычислительным
экспериментом прослеживаются определенные
внешние гомологии. Как и развивающийся эмбрион,
растущая клеточная фигура на начальном этапе
игры принимает круглую форму. Затем внутри
образовавшейся округлой области начинают
происходить формообразовательные процессы. По
мере разрастания клеточная конфигурация
усложняется, приобретая все большее количество
декоративных деталей. При этом ее форма остается
строго правильной и симметричной. Это
объясняется тем, что процесс дифференцировки
растущей клеточной структуры протекает по
одинаковым правилам во всех направлениях, и в
результате образуются только симметричные
конфигурации. А.КОЛЕСНИКОВ, |
| Автор | )c( 2000-2019 Kопирайта нет, копируйте на здоровье :) 100112 лет в Интернете |
|
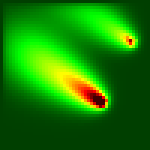 При этом высокие значения
концентраций изображаются оттенками красного,
который, по мере снижения Z, переходит в желтый, а
затем постепенно затухает до темно-зеленого
цвета (подробнее о цветовых гаммах и
визуализации графиков см. "КВ" №
При этом высокие значения
концентраций изображаются оттенками красного,
который, по мере снижения Z, переходит в желтый, а
затем постепенно затухает до темно-зеленого
цвета (подробнее о цветовых гаммах и
визуализации графиков см. "КВ" № Описанный
алгоритм порождает бесконечное множество
неповторяющихся сложных геометрических фигур,
которые можно было бы назвать клеточными
симметроидами. Порой они напоминают диковинные
цветы, порой - тело медузы, некоторые похожи на
витражи средневековых соборов, орнаменты
восточных ковров или магические символы.
Описанный
алгоритм порождает бесконечное множество
неповторяющихся сложных геометрических фигур,
которые можно было бы назвать клеточными
симметроидами. Порой они напоминают диковинные
цветы, порой - тело медузы, некоторые похожи на
витражи средневековых соборов, орнаменты
восточных ковров или магические символы.  На иллюстрациях приведены
черно-белые изображения. При желании их можно
раскрасить, использовав к примеру материал
статьи в
На иллюстрациях приведены
черно-белые изображения. При желании их можно
раскрасить, использовав к примеру материал
статьи в