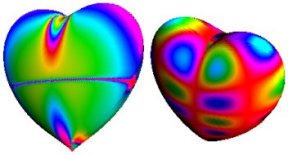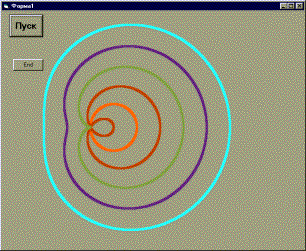
Улитка на паутине в стиле Поп-Арт

Виток первый, исторический.

В каждом справочнике по математике в разделе «Замечательные кривые» непременно присутствует Улитка Паскаля. Вроде бы ничего удивительного - с этим именем связано много открытий. Но в многочисленных источниках мы встретим фразы вроде «Улитка Паскаля названа так не в честь того самого Блеза Паскаля, а в честь его отца Этьена Паскаля, любителя математики, впервые описавшего эту кривую». Замечательный пример гениальности семейства, опровергающий расхожее утверждение о том, что на детях природа отдыхает. В 1638 г. Этьен Паскаль возглавил группу недовольных рантье, протестовавших против решения правительства отменить выплату ренты, и кардинал Ришелье приказал упрятать бунтовщика в Бастилию. Паскалю пришлось бежать, и дети остались в Париже одни. Однако после интригующей истории, описанной на http://schools.techno.ru/sch444/MUSEUM/PRES/PL-4-98.htm,   Ришелье обещал дочери смутьяна прощение для ее отца. Кардинал сдержал свое слово: Этьен Паскаль был прощен и назначен на пост интенданта Руанского генеральства. В Руан семейство Паскалей прибыло 2 января 1640 г., и Э. Паскаль сразу же погрузился в работу. Он ночи напролет просиживал над подсчетами налоговых сборов. Блез помогал отцу. Впоследствии он писал, что начал работу над арифметической машиной, желая облегчить громоздкие вычисления, которые он делал для отца. Но, получается, Этьен Паскаль не только подсчитывал налоги, но и занимался математическими исследованиями, одно из которых обессмертило его имя.

Чем же так интересна Улитка Паскаля, что попала во все справочники? Сейчас мы расскажем о ней и вы сами ответите на этот вопрос. Для разминки небольшая шуточная задача: «Если монета катится по неподвижной монете такого же диаметра, то сколько раз она обернется вокруг своей оси за один оборот вокруг монеты?». Не торопитесь с ответом - первое пришедшее на ум решение чаще всего ошибочное, ответ и связь его с Улиткой Паскаля рассмотрим позже. Уравнение Улитки имеет вид (x²+y²-ax)²=b²(x²+y²) - это уравнение четвертой степени, для построения графика функции практически не пригодное, так как попытка выразить y через x приведет к необычайно громоздким построениям. Однако нам известна формула Улитки в полярных координатах r=b+acos(fi).

Виток второй. Полярный.

Небольшое отступление. Это просто чудо - полярные координаты - для любителей математических картинок. Даже если рисовать на миллиметровке, рассчитывая координаты с помощью таблиц Брадиса, памятных тем, кто учился в «докалькуляторную» эпоху. Простейшая зависимость r=RSin(fi) нарисует восьмерку, r=RSin (2*fi) - четыре лепестка, r=RSin (4*fi) - восемь, а r=R-RSin (4*fi) вычтет эти лепестки из круга. А если добавить сомножителей и слагаемых с разными коэффициентами для амплитуд и для фаз (в разных степенях…), то каждый раз будут получаться цветы и розетки невиданной красоты. И просторы для экспериментов безграничны - можно получить, подобрав уравнение, цветок сирени или листок крапивы, Чебурашку или «взрыв на макаронной фабрике». А если сделать цвет зависимым от текущего радиуса… или от угла… то оторваться от забавы будет невозможно. Напомню, что полярные координаты переводятся в прямоугольные очень даже просто: x=Rcos(fi) и y=Rsin(fi). С тем, что у экранных координат ось y направлена вниз вы справитесь за 5 секунд. Вернемся к нашим Улиткам. Рассмотрим уравнение r=b+acos(fi). Зная, что уравнение r=b нарисует окружность, а уравнение r=acos(?) - восьмерку, мы уже знаем, чего ожидать - это будет окружность, из которой вычли восьмерку, и в зависимости от соотношения параметров a и b нечто яблочно-однобокое. Осталось только убедиться в этом.

Private Sub Комманда1_Click() Cls : pi = 4 * Atn(1) scal = 15 a = 100 DrawWidth = 5 For l = 0 To 2 Step 0.5 For t = 0 To 360 Step 0.25 tt = t * pi / 180 ll = l * a rr = a * Cos(tt) + ll x = rr * Cos(tt): y = rr * Sin(tt) Col = RGB(255 - 100 * l, 128 + (-1) ^ (l * 2) * l * 60, l * 120) Line (x + 190, y + 250)-Step(ss, ss), Col, BF Next t Next l End Sub Private Sub Комманда2_Click() End End Sub

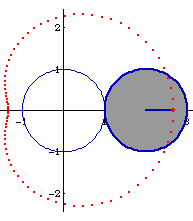
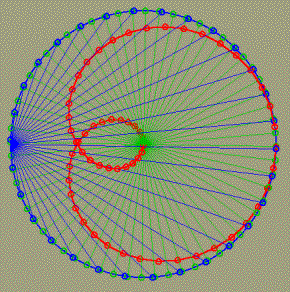
В нашем примере a=100 - величина постоянная, а b меняется в цикле от b=0 до b=2a (вспомогательная переменная ll). Для b=0 я обещал восьмерку, но нарисована только алая окружность - тут нет жульничества, дело в том, что косинус функция четная, поэтому оба витка восьмерки слились в один. В том, что это действительно так убеждаемся при рассмотрении случая b=0.5a - темно-красная линия показывает, как эти два витка разъединились - один стал больше, а другой меньше. Следующий шаг для случая b=a (зеленая линия) является самым характерным - меньшая петля вырождается в точку, а большая удваивает свой радиус, полученная фигура называется кардиоидой и часто встречается в самых непредвиденных случаях, мы к ней еще вернемся. При увеличении b до 1.5a (фиолетовая линия) и до 2a (голубая линия) от меньшего локона остается впадинка, которая при увеличении b постепенно сглаживается. Это и есть семейство кривых Улитки Паскаля для разных соотношений a и b. Обратите внимание, как получена раскраска линий в разные цвета - если красная составляющая цвета линии убывает, а синяя растет с ростом переменной l, то зеленая составляющая цвета то растет, то уменьшается, позволяя создать пеструю картинку.

Виток третий. Этюд в багровых тонах.

Небольшой подарок тем, кто терпеть не может математику, но любит красивые изображения.

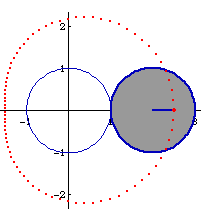
Причем получен рисунок минимальной доработкой предыдущей программы - переменная l меняется в цикле и от нее зависят соотношения a и b и цвет выводимой линии. Меняя толщину линии (DrawWidth = 8) можно изменять и неожиданно появившийся эффект горизонтальных и вертикальных блестящих полос, а меняя коэффициенты при задании цветовых составляющих получать картины по вашему вкусу.

Private Sub Комманда1_Click() Cls pi = 4 * Atn(1) scal = 15 a = 140 DrawWidth = 8 For l = 0 To 220 Step 5 * ss For t = 0 To 360 Step 0.25 tt = t * pi / 180 x = a * Cos(tt) ^ 2 + l * Cos(tt) y = a * Cos(tt) * Sin(tt) + l * Sin(tt) red = 255 - 250 * Sin(0.31 * l) green = 255 - 250 * Sin(0.3 * l) blue = 255 - 250 * Sin(0.29 * l) Col = RGB(red, green, blue) If l Mod 2 = 0 Then Col = RGB(0, 0, 0) Else Col = RGB(255, l, 255 - l) End If If ss > 1 Then Line (x + 190, y + 250)-Step(ss, ss), Col, BF If ss = 1 Then PSet (x + 190, y + 250), Col Next t Next l End Sub Private Sub Комманда2_Click() End End Sub

Вернемся к параметрам Улитки a и b. Это не что иное, как радиуса окружностей, катящихся друг по другу, причем, b - это радиуса как таковые, по которым и происходит качение а «a» - это радиус, на котором лежит точка катящегося интересующей нас траектории, если он меньше радиуса колеса, то траектория будет гладкой, если больше, то появляются петли, а если равен, то петли в точке касания превращаются в точку, рисуя кардиоиду. Это хорошо видно на картинах, полученных с http://www.xahlee.org/SpecialPlaneCurves_dir/LimaconGGallery_dir/limaconGGallery.html  

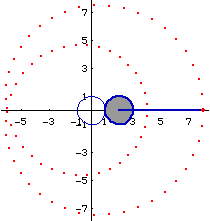
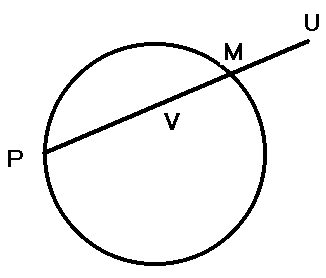
При первой возможности рассмотрите и другие картинки на этой странице. Напомним также, что приведенные картинки называются циклоидами (а точнее, эпициклоидами) и сами по себе являются источниками целого класса задач и компьютерных развлечений. Подробнее о циклоидах смотрите здесь  

Виток четвертый. Конхоида.

Рассмотрим красивую задачу - представим Улитку Паскаля как конхоиду. Не углубляясь в теорию кривых, дадим такое нестрогое определение: конхоида - это геометрическое место точек, полученное перемещением каждой точки первоначальной кривой вдоль определенным образом заданных поверхностей. Для Улитки Паскаля первоначальной кривой служит самая обычная окружность, а переносятся точки вдоль линий, проходящих через точку, лежащую на этой окружности. Поясним графически. На рисунке мы выбираем на окружности неподвижную точку Р и переменную точку М, которую мы сдвигаем вдоль линии, соединяющей точки Р и М на какое-то фиксированное расстояние а.

Полученные семейства точек V и U и есть конхоида окружности относительно фиксированной точки. Программа, реализующая эту модель скромна до неприличия, но позволяет получить ожидаемые картинки. Сначала назначим а=0.25R. Обратите внимание на необходимость сделать два оборота (центральный угол, он же переменная f от 0 до 720 градусов) - один сдвигает точки наружу, а второй оборот - внутрь окружности.

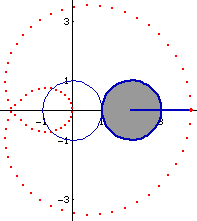
Для а=0,5R

Для а=R

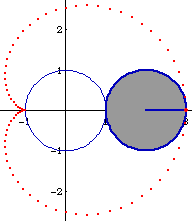
Для а=2R

Для а=3R

Код к рисункам, точнее, к рисунку для случая a=R:

Cls pi = 4 * Atn(1) scal = 15 r = 120 a = 1 * r For f = 1 To 720 Step 6 t = f * pi / 180 X = r * (1 + Cos(t)) Y = r * Sin(t) alfa = 0 If X > 0 Then alfa = Atn(Y / X) If f <360 Then X1=X+ a * Cos(alfa) Y1=Y+ a * Sin(alfa) Else X1=X + a * Cos(alfa) Y1=Y + a * Sin(alfa) End If red=255 green=0 blue=0 col=RGB(red, green, blue) DrawWidth=2 Circle (X1 + 190, Y1 + 250), 2, col Circle (X + 190, Y + 250), 2, RGB(0, 155, 150) Line (X + 190, Y + 250)-(X1 + 190, Y1 + 250), RGB(0, 155, 0) Next f End Sub </p>

Основная тонкость переход от центрального угла окружности, по которому мы проходим в цикле (переменные f в градусах или t в радианах), к углу линии, соединяющей постоянную точку с текущей на окружности c горизонтальной осью (переменная alfa). Теперь вы знаете, что такое конхоида на случай участия в какой-либо телеигре или разгадывания кроссворда.

Виток пятый. С фантазией.

Следующий шаг скорее занимательный, направленный на получение изображения Улитки Паскаля, которое при некоторой фантазии можно увязать с анекдотом, заканчивающимся фразой: «Доктор, откуда у вас такие картинки?»

Cls pi=4 * Atn(1) scal=15 a=140 DrawWidth=4 For l=0 To 1.2 Step 0.01 For t=0 To 360 Step 0.25 tt=t * pi / 180 ll=l * a rr=a * Cos(tt) + ll x=rr * Cos(tt): y=rr * Sin(tt) xx=x / 4000: yy=y / 4000 k=(xx * xx + yy * yy a * xx) ^ 2- ll ^ 2 * (xx ^ 2 + yy ^ 2) red=Abs(254- 10.75 * k) Mod 255 green= Abs(254- 13 * k) Mod 255 blue= Abs(255- 15.25 * k) Mod 255 Col=RGB(red, green, blue) Line (x + 190, y + 250)-Step(ss, ss), Col, BF Next t Next l </p>

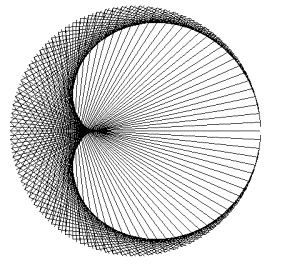
Здесь был использован прием, позволяющий на основе уравнений получать красивые изображения. Перепишем уравнение Улитки Паскаля (x²+y²-ax)²=b²(x²+y²), перенеся правую часть налево от знака равенства, и приравняем полученное выражение не нулю, как это напрашивается по канонам математики, а некоторой переменной k. Теперь нарисуем в цикле серию Улиток, как мы делали в начале статьи, но заполняя всю плоскость, задав шаг почаще и линии потолще, а главное, задавая цвет (его красную, зеленую и синюю составляющие) в зависимости от значения k. Причем, эту зависимость можно подбирать опытным путем, добиваясь красивых изображений.

Виток шестой. Педальный.

Определение педальной кривой для первоначальной давать не будем, сразу перейдем к делу. В текущей точке окружности (пробегаемой в цикле по всей окружности) проведем касательную линию, а потом из фиксированной точки (в нашем случае лежащей на окружности) проводим перпендикуляр к этой касательной. Совокупность этих перпендикуляров огибает, как вы уже догадались, кардиоиду. Это в частном случае расположения фиксированной точки на окружности, при смещении этой точки внутрь окружности или наружу ее получим все семейство Улитки Паскаля.

Cls pi=4 * Atn(1) scal=15 r=180 a=0 * r DrawWidth=1 Circle (190 + r, 250), r, RGB(0, 0, 200) For f=1 To 720 Step 3 t=f * pi / 180 x=r * (1 + Cos(t)) y=r * Sin(t) beta=pi / 2 + t k= Tan(beta) b=y- k * x k1=-1 / k b1=k1 * a X1=(b1- b) / (k -k1) Y1=k1 * X1 + b1 red=255 green=0 blue=0 col=RGB(red, green, blue) Circle (X1 + 190, Y1 + 250), 3, col ' Точка пересечения красная Circle (x + 190, y + 250), 3, RGB(0, 155, 150) 'Точка на круге голубая Line (190 a, 250)-(X1 + 190, Y1 + 250), RGB(0, 155, 0) Line (x + 190, y + 250)-(X1 + 190, Y1 + 250), RGB(0, 55, 150) Next f

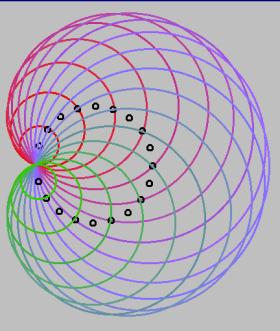
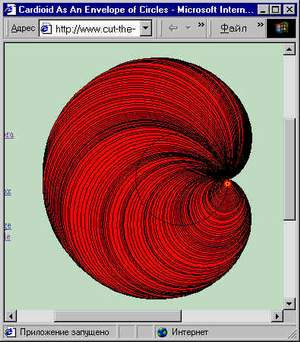
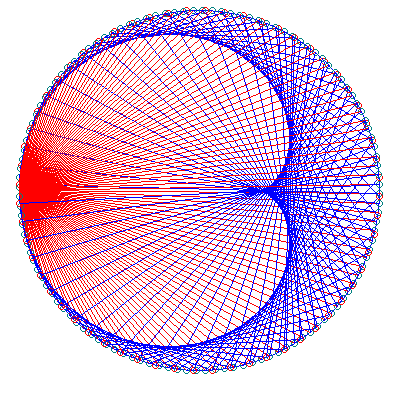
В приведенной программе все также счетчик цикла f центральный угол в градусах, t он же в радианах, beta угол наклона касательной в соответствующей точке цикла, k тангенс этого угла. Уравнение лини, как известно, y=kx+b, для каждой касательной находим b=y-kx. Для взаимно перпендикулярных прямых k1=-1/k, а b1=0 так как все перпендикуляры проходят через точку у которой y= 0. Решая совместно уравнения касательной и перпендикуляра к ней, находим координаты точки пересечения и рисуем в них маленький красный кружок. Эти кружки и нарисуют нам педальную кривую к окружности относительно точки.

Виток седьмой. Энвелопа окружности или осторожно осы!

Будем брать точки все на той же нашей окружности, ставить в них иголку циркуля и рисовать новые окружности так, чтобы они все проходили через все ту же фиксированную точку на окружности. Общая огибающая (так называемая энвелопа) к полученным окружностям будет конечно, все уже догадались кардиоидой. А при смещении фиксированной точки получим всю гамму Улиток Паскаля. Этот процесс иллюстрирует картинка и программа, нарисовавшая ее. Маленькими черными кружками отмечены лежащие на исходной окружности точки центры проводимых окружностей.

Private Sub Комманда1_Click() Cls pi= 4 * Atn(1) scal= 15 r= 90 a= 0 * r DrawWidth= 3 For f= 1 To 360 Step 18 t= f * pi / 180 + pi x= r * (1 + Cos(t)) y= r * Sin(t) rr= Sqr((x a) ^ 2 + y ^ 2) red= 255 0.6 * f green= 0.6 * f blue= Abs(Int(0.0005 * f * (360 f))) ^ 2 col= RGB(red, green, blue) Circle (190 + x, 250 + y), rr, col Circle (x + 190, y + 250), 4, RGB(0, 0, 0) Next f

Здесь а смешение фиксированной точки для ваших экспериментов, пока равно нулю. Главное в этой программе посчитать радиус рисуемой в каждой точке цикла окружности, хотя для этого достаточно теоремы Пифагора, надо только уметь ее применить к месту. Как вы уже заметили, расцветка красивая, цвет окружностей меняется в течение цикла. Достаточно всего лишь уменьшить шаг цикла и мы получим красивую картину.

Теперь нас отделяет от создания шедевра один маленький шаг делаем толщину линии побольше (например, 55 пикселей или, как иногда пишут, пикселов) и раскрашиваем каждый четный круг в желтый цвет, а нечетный в черный. И получаем шедевр поп-арта, которому позавидовал бы сам Малевич.

Чем-то смахивает на осу, и вообще желтый с черным это сигнал об опасности, тем, кто будет повторять эти опыты лучше подобрать более спокойные сочетания цветов.

Cls pi=4* Atn(1) scal=5 r=88 a=0 * r DrawWidth=55 For f=1 To 360 Step 17 t=f * pi / 180 + pi x=r * (1 + Cos(t)) y=r * Sin(t) rr=Sqr((x- a) ^ 2 + y ^ 2) If f Mod 2=0 Then col=RGB(255, 255, 10) Else col=RGB(0, 0, 0) End If Circle (190 + x, 260 + y), rr, col Next f

Как выделить четные шаги мы проходили неоднократно в прошлых публикациях достаточно сравнить с нулем модуль (остаток) от деления на два. Если вы побываете на страничке профессора математики университета Айовы Александра Богомольного (http://www.cut-the-knot/pithagorfas/cycloids.html ), то найдете симпатичный аплет, рисующий кардиоиду.

Причем, как мы теперь знаем, именно методом рассмотренной только что энвелопы.

Виток восьмой. Скромный. Серединки.

Продолжим наши опыты. Для текущей точки на окружности выделяем центральный угол с горизонтальной осью, под таким же углом проводим луч из фиксированной точки (все той же, на окружности), до пересечения с окружностью. Точку пересечения луча с окружностью соединяем с первоначальной точкой и находим середину полученной хорды. Вы будете смеяться, но эти середины хорд лежат на Улитке Паскаля.

Текущий центральный угол нам выделять не надо мы и так от него в цикле все и строим. Единственный технический момент нахождение точки пересечения окружности и линии, проходящей через фиксированную точку (параллельно радиусу, проведенному в текущую точку). Кому стало скучно, могут пропустить эти пояснения. Я проработал двадцать лет разрабатывая и внедряя программы на станках с ЧПУ, и поэтому воспринимаю аналитическую геометрию как райскую музыку. Для нахождения координат точки пересечения линии, проходящей через фиксированную точку и окружности, надо совместно решить их уравнения. Уравнение линии y=kx+b, причем b=0 так как точка лежит на оси x, а k=tan(t), где t угол наклона линии в радианах. А уравнение окружности (x-r)²+y²=r² так как центр сдвинут на величину r относительно начала координат, проходящего через фиксированную точку. Исключив y и решив относительно x, получим x=2r/(1-k²). Подставив это значение в уравнение линии, получим y точки на круге. А уж зная координаты двух точек найти координаты середины соединяющего их отрезка совсем просто они равны полусумме координат точек. Все это и реализовано в приведенной программе.

Cls < pi= 4 * Atn(1) r= 200 DrawWidth= 2 Circle (190 + r, 250), r, RGB(0, 0, 200) x3= 2 * r: y3= 0 For f= 1 To 360 Step 6 t= f * pi / 180 x= r * (1 + Cos(t)) y= r * Sin(t) k= Tan(t) X1= 2 * r / (1 + k ^ 2) Y1= k * X1 X2= (X1 + x) / 2: Y2= (Y1 + y) / 2 DrawWidth= 2 Circle (X1 + 190, Y1 + 250), 4, RGB(0, 0, 250) Circle (x + 190, y + 250), 4, RGB(0, 205, 0) Circle (X2 + 190, Y2 + 250), 4, RGB(250, 0, 0) Line (X2 + 190, Y2 + 250)-(x3 + 190, y3 + 250), RGB(250, 0, 0) DrawWidth= 1 Line (190, 250)-(X1 + 190, Y1 + 250), RGB(0, 0, 250) Line (190 + r, 250)-(x + 190, y + 250), RGB(0, 205, 0) x3= X2: y3= Y2 Next f

В отличие от предыдущих опытов мы не получили кардиоиду. Задание на дом для тех, кто думает, что что-то понял: где должна лежать фиксированная точка, чтобы у нас получилась кардиоида?

Виток девятый. Акустический.

Недавно вычитал в Сети, что если орать изо всех сил в течение 11 лет, то выделившейся энергии хватит, чтобы разогреть порцию вермишели. А нельзя ли здесь сэкономить? Не для того, чтобы орать не 11 лет, а, скажем, 10, а вообще, рассмотреть распространение волн и найти закономерности. Если мы заглянем в цилиндрический зал и крикнем, то наверняка будут точки, в которые звук наш прилетит громче, чем в какие-то другие. Во всяком случае, мы можем построить модель распространения волн в цилиндрической комнате, или, что тоже самое, лучей в окружности, причем, будем рассматривать только первый отраженный луч. Вы, даже не читая дальше, поспорите, что отраженные лучи дадут кардиоиду. И будете совершенно правы! Из уважения к читателям программу не привожу после стольких тренировок не написать ее просто неприлично. Единственное, что нужно помнить, что угол падения равен углу отражения и что внутренний угол вдвое меньше центрального угла, опирающегося на ту же дугу.

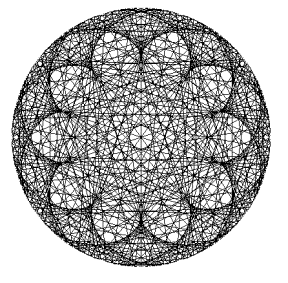
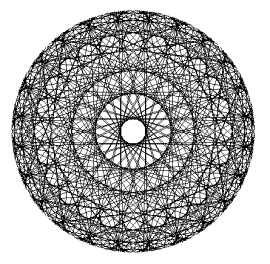
Судя по картинке человек, стоящий в узле кардиоиды просто оглохнет от слова, сказанного еле слышным шепотом у противоположной стены. Однако уже слышны возмущенные крики (нет, не из нашей круглой комнаты) защитников чистой физики. Во-первых, все лучи проходят разной длины путь, поэтому в узловой точке будет слышна не речь, а размазанная какофония. Во-вторых, по той же причине волны в узел кардиоиды будут приходить в разных фазах и поэтому будут частично гасить друг друга. Если действительно построить интеренференционную картину волн в окружности от точечного источника, то среди выявленных узлов вполне может оказаться и полюс кардиоиды. И, в-третьих, мы не построили третьи, четвертые и так далее отраженные волны, неизвестно еще, как они повлияют на наш «подогрев вермишели». Хотя есть какое то предчувствие того, что третьи и дальнейшие лучи тоже лягут по знакомым нам кривым, предлагаю желающим проверить. А как насчет покричать в сфере сохранится ли аналогия в трехмерном пространстве? Осталось только сказать, что семейства кривых, построенные как огибающие прямых, построенных по законам распространения волн, называются каустиками. То есть, каустиком окружности является кардиоида.

Виток десятый. Паутинный.

Любителям математических картинок известна так называемая паутина. На окружности берутся точки с определенным шагом, и каждая из них соединяется с такой же точкой, но сдвинутой по фазе в какое-то число раз (n). Это число можно задавать или брать случайным образом. Точки пересечения хорд сливаются в муаровый узор самых замысловатых форм. Идея так притягательна, что настоятельно рекомендую всем попробовать реализовать ее самостоятельно, чтобы поиграть с параметрами и насладиться эффектами. При n= 1 не нарисуется ничего, так как начальные и конечные точки линий совпадают, зато при увеличении n будут появляться фигуры с узлами, причем количество узлов равно n-1. Нас же особенно интересует случай для n= 2, при этом нарисуется фигура, хорошо уже изученная нами кардиоида. При n= 3 так называемая нефроида с двумя узлами. Если n-1 делитель числа 360, то картинка проявляет некоторую упорядоченность. Приводим картинки для значений n= 2 (наша любимая кардиоида) и для сравнения две паутины для значений n= 111 и n= 25.

Код для паутин

n= 2 'n= 111 xx= 380 yy= 380 R= 200 P= 3.1415926 Cls For i= 0 To 360 Step 1 T= i * P / 180 x= R * Cos(T) y= R * Sin(T) X2= R * Cos(n * T) Y2= R * Sin(n * T) c= 255 / 360 Line (x + xx, y + yy)-(X2 + xx, Y2 + yy), RGB(0, 0, 0) Next i

Эта модель позволяет реализовать множество забав. Во-первых, меняем n в цикле (желательно с нуля и с малым шагом), перерисовываем заново, и нашему взору предстает изумительная картина. Справа все время рождаются узлы и, постепенно замедляясь и теснясь, движутся против часовой стрелки. Внезапно появляются купола, движущиеся от периферии к центру и, прежде чем исчезнуть, на мгновение превращающиеся в концентрические кольца. Кроме того, постоянно движутся концентрические зоны, меняя скорость и направление, порождают фантастические узоры из узлов. Особенно «повезло» близоруким: сняв очки, они увидят пульсирующий Солярис, постоянно собирающийся в меняющиеся узоры. Во-вторых можно без конца менять количество, толщину линий и их цвет в зависимости от счетчика цикла. В третьих, можно запустить процесс не на окружности, а на фигурах Лиссажу, или начальные точки на окружности, а конечные на фигуре Лиссажу, или наоборот. Подробнее об удивительной паутине читайте на http://arbuz.ferghana.ru/z_pauk.html  

Виток одиннадцатый. Заключительный.

Вообще не понятно, почему эта кривая называется Улиткой на англо- и франкоязычных сайтах применяется латинское Limacon. Если программировать лень, а поиграть с Улиткой хочется, то на http://www-groups.dcs.st-andrews.ac.uk/~history/Java/Limacon.html   вы найдете симпатичный аплет, рисующий Улитку с заданными из формы параметрами. А на странице http://www.sciencenews.org/20020209/mathtrek.asp   вы найдете доработку кардиоид в выходом в третье измерение получаются настоящие сердца. Кому не хватает сердца, как Железному Дровосеку, могут использовать красивое виртуальное. Выбирайте.

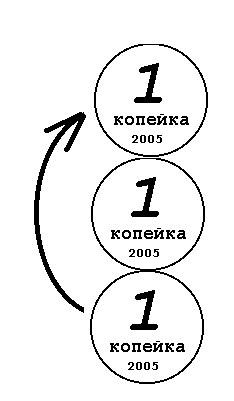
И, наконец, вернемся к задачах о монетах, которые добросовестные читатели решали во время чтения статьи. Первое пришедшее в голову решение, что монета, катясь по такой же монете, при обходе поворачивается на один оборот, будет неверным!

Посмотрите на картинку и проверьте лично: при обкатывании из нижнего положения в верхнее монета сделает (как ни странно) полный оборот, а, значит, при полном обкатывании два оборота! Один оборот сделает в этом случае центр катящейся монеты, а ведь она еще и катится вокруг него. Те, кто знаком с курсом «Теории механизмов и машин» найдут здесь подобие дифференциала. Теперь вы легко найдете количество оборотов вокруг монеты с вдвое большим радиусом и вокруг двух касающихся монет. Есть красивая теорема о том, что количество оборотов монеты при обкатывании нескольких касающихся монет не зависит от взаимной конфигурации этих нескольких монет, проверьте! А связь этих всех монет с сегодняшней темой в том, что точка катящейся монеты отписывает кардиоиду. И, напоследок, решите задачу, из коллекции Гарднера: девушка с круглой талией вращает обруч вдвое большего (чем талия) радиуса. Какое расстояние (в радиусах талии) пролетит точка, коснувшаяся пупка до следующего с ним соприкосновения? Траектория этой точки описывает линию, которая является, конечно же, кардиоидой. На этой приятной картине и закончим.