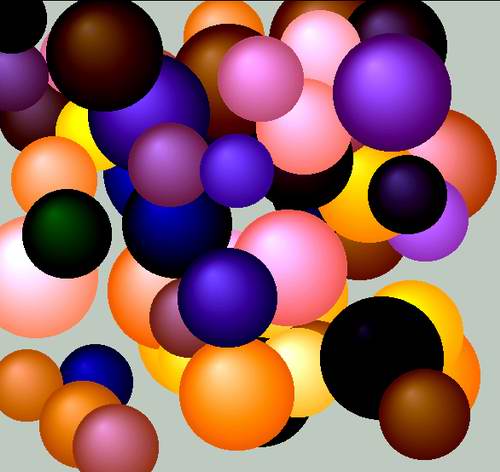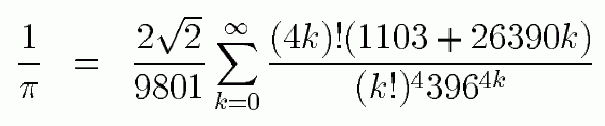|
Пилюли для Пигмалиона
и воздушная кукуруза
|
Опубликовано в
Hard'n'Soft №4 2003 |
История повторяется – видимо, историки
обделены фантазией.
Станислав Ежи Лец
Прав язвительный автор – все как
в его афоризме, вынесенном в эпиграф, мы снова
возвращаемся к числу Пи. Казалось, что
предыдущими публикациями пройдены все тропинки
в этом сказочном лесу и обглоданы все вкусные
косточки волшебного числа, но, как-то сами
появляются новые программы, картинки и забавные
сведения.
Например, проявляется некоторая привязанность
числа Пи к номеру 5: первые 5 десятичных чисел дают
в сумме 20, первые 20 сумм 5x20=100. Самое замечательное
же происходит с 761-м числом Пи – с этого места
идут подряд шесть девяток. (Мы писали об этом в №3
2002, а все публикации найдете в «Зоне Пи»
на
Там же в Клубе Пи можете рассмотреть все (ну
почти все) цифры Пи). Число 761 в некотором роде
вообще интересное и связано, как и 5, с Пи
невидимыми нитями. Число 5, к тому же, является
цифровым корнем числа 761 (7+6+1=14, 1+4=5). А если сложить
факториалы цифр числа 761: 7! +6! +1! =5761, то получаем то
же самое число, которому предшествует его
цифровой корень. (Есть числа, сумма факториалов
цифр которых равна числу с приписанным впереди
числовым корнем, и есть математики, занимающиеся
поиском этих чисел.)
Еще красивая теорема: «Если сумма двух чисел
равна 1000 и одно из этих чисел имеет цифровой
корень равный 5, то второе число также имеет
цифровой корень, равный 5. Это справедливо только
для 1000. Всего таких пар 110, но только одна из них
состоит их двух простых чисел: 761 и 239. И еще
особенность: 5761/761-6=5*(239/761)=1.5703022. Обратите
внимание, что 10*(239/761) =3.1406 … единственная из 55 пар,
которая дает самое близкое приближение Пи, с 3
правильными цифрами.
Если мы пытаемся найти приближенное Пи как
22/7=3.142857 142857 …, периодической дробью с периодом 6,
то на 761 месте стоит 5, причем, на пятом месте в 127м
периоде (127=2^7-1 – седьмое число Мерсенна).
Обратите внимание, между прочим, как инверсия 22/7
дает скорость света: с=sqr(7/22*3^24)=299733км/сек, что
всего на 19км/сек меньше теоретического значения
(конечно же из-за космической пыли, уверен автор
этой находки на http://www.terravista.pt/guincho/1219/1a_index_uk.htm ).
Число Пи имеет также любопытные соотношения с 3 и
7: первые 3 десятичных числа дают в сумме 6, первое
совершенное число, а первые 7 цифр дают в сумме 28
– второе совершенное число и треугольное число
номер 7. И, наконец, 9961-ое десятичное число Пи – 6 и
три девятки, что указывает на некоторую
избранность числа 9961, оно делится на 7, сумма
факториалов его цифр тоже делится на 7, и
9961-5761=4200=7x6x1x100.
Если вдруг вы надумаете писать программу для
проверки предложенных находок, то легко
справитесь с вычислением цифрового корня числа
– превращаете число в строковую переменную,
выделяете в цикле по одному символу, переводите в
числовой формат и суммируете. Если конечная
сумма больше 9, то процесс повторяем.
Эта задача перекликается с «Отгадывателем
мыслей» (можете рассмотреть
текст Java-script) в котором вас просят задумать
двузначное число, отнять от него сумму его цифр,
полученное число найти в таблице и запомнить
символ рядом с ним. После щелкаете по волшебному
квадратику и в нем появляется тот самый символ,
который стоял рядом с вашим числом. Первые
несколько минут игрушка вызывает панический
ужас – как этот ящик узнал задуманное!?! Но,
постепенно, соображаем, что если от двузначного
числа отнять сумму его цифр, то всегда будет
получаться число, кратное 9. { 10*x+y-(x+y)=9*x, например,
78-(7+8)=63 }. А у всех чисел, кратных 9 одни и те же
символы, но при каждом сеансе разные.
Один из постоянных посетителей Арбуза подсказал
адрес еще одного прикольного «Угадывателя» (http://www.caveofmagic.com/zickcrd1.htm)
- на экране появляются несколько карт, картинки –
вальты, дамы, короли разных мастей, просят
сконцентрироваться на одной из них и потом
щелкнуть «Дальше», появятся снова несколько
карт, среди которых нет задуманной. Это
впечатляет, пока, после нескольких сеансов, не
сообразите, что во второй порции карт нет ни
одной карты из первой порции – то есть, все равно
на чем концентрироваться.
Одна из самых притягательных задач для любителей
математики – получить красивые картинки
основываясь на цифрах числа Пи. В Интернете есть
такие изображения, мы уже писали о них, но хочется
ведь самодельных шедевров. Начнем с технологии –
как нарисовать объемный шар? Если задать круг с
заливкой цветом, то это и останется плоский круг
с заливкой – ничего интересного. Поэтому
воспользуемся приемом – задаем толщину линий
побольше, 4 или 5 пикселей (Picture1.DrawWidth=4) и рисуем
окружность выбранным цветом без заливки. Теперь
смещаем центр на несколько пикселей вверх и
влево, увеличиваем яркость цвета и рисуем еще
окружность, эту процедуру повторяем, пока радиус
не выродится в нуль. Подобрав смещение центра и
увеличение яркости, мы получим красивейший
объемный шар, буквально выпирающий из монитора.
Играя коэффициентами изменения цвета и прочими
параметрами можно получать как блестящие яркие
новогодние игрушки, так и матово-костяные
бильярдные шары. Причем, каждый шар красив
по-своему, хочется сохранить каждый вариант,
поэтому единственный способ насладиться этой
забавой – насыпать много шаров с разными
случайными параметрами.

Текст программы (фрагмент):
Видно, что реализовано не совсем
так, как описано выше, круги рисуются в цикле от
единичного радиуса до радиуса шара, а цвет
меняется от белого до цвета шара.
Налюбовавшись на шары, думаем, что из них можно
соорудить. Конечно же, модели молекул, розетку с
зернистой икрой, виноградную кисть и …
кукурузный початок. На фоне шаров, естественно.

Фрагмент кода для початка.
Кстати, знакомый по переписке,
активный участник Арбузных экспериментов,
прислал скринсейвер с шарами – пузырями, они
всплывают, тонут, лопаются и рождаются снова.
Причем не просто шары, а, как выразился автор, это
корм для Таканов, ведь они все зеленого цвета. Кто
такие Таканы читатели помнят по рассказу в
сентябрьском номере журнала. Подробности и саму
программу найдете здесь. Оцените
и поддержите идею, присылайте корм для Таканов,
они будут рады.
Теперь мы во всеоружии, готовы к тому, чтобы
заняться визуализацией числа Пи.
В приводимом листинге программы в начале
проведены некоторые подготовительные действия.
Чтобы быстрее заняться непосредственно
рисунком, я перенес первые 720 цифр числа Пи прямо
в текст программы, как они были в файле html с
пробелами через каждые 10 цифр. Точку после тройки
удалил сам, а для удаления пробелов пришлось
сделать «перекидку» из массива «а» в массив «с» с
удалением пробелов. Для более серьезного
занятиями с цифрами Пи такой метод не очень
годиться, если вы захотите использовать десятки
или сотни тысяч известных знаков, то, конечно,
лучше открыть файл со знаками и считывать из
него. Здесь используется функция выделения
символов из строки mid(m,n,k), где m – имя исходной
строки символов, n – номер символа, с которого
надо начинать выделение и k – количество
выделяемых символов. Например, q=”победа” w=mid(q,3,4)
присвоит q “беда”. (Кстати, на страничке «Visual Basic на русском», автор
которой дал много ценных советов и замечаний по
программному содержанию Арбуза, расположен
хороший файл – «help» по функциям этого языка,
рекомендую.)
Дальнейшее должно быть понятно: в цикле
рассматриваем по 12 символов, из которых первые
три определяют координату центра по горизонтали,
вторые три – по вертикали, следующие две цифры
определяют радиус шара, из следующих оставшихся
четырех формируется цвет шара. А как сделать шар
объемным мы уже рассмотрели.
Dim pi As Double, i As Integer, a As String
a = "31415926535 8979323846 2643383279 5028841971" + _
"6939937510 5820974944 5923078164 0628620899" + _
"8628034825 3421170679 8214808651 3282306647" + _
"0938446095 5058223172 5359408128 4811174502" + _
"8410270193 8521105559 6446229489 5493038196" + _
"4428810975 6659334461 2847564823 3786783165" + _
"2712019091 4564856692 3460348610 4543266482" + _
"1339360726 0249141273 7245870066 0631558817" + _
"4881520920 9628292540 9171536436 7892590360" + _
"0113305305 4882046652 1384146951 9415116094" + _
"3305727036 5759591953 0921861173 8193261179" + _
"3105118548 0744623799 6274956735 1885752724" + _
"8912279381 8301194912 9833673362 4406566430" + _
"8602139494 6395224737 1907021798 6094370277" + _
"0539217176 2931767523 8467481846 7669405132" + _
"0005681271 4526356082 7785771342 7577896091" + _
"7363717872 1468440901 2249534301 4654958537" + _
"1050792279 6892589235 4201995611 2129021960"
c = ""
For i = 1 To 720
b = Mid(a, i, 1)
If b <> " " Then c = c + b
Next i
Picture2.DrawWidth = 3
For z = 1 To 708 step 12
x = Val(Mid(c, z, 3)) / 2
y = Val(Mid(c, z + 3, 3)) / 2
r = Val(Mid(c, z + 6, 2)) / 3 + 40
co = Mid(c, z + 8, 4)
re = Int(Val(co) / 20)
gr = Val(Mid(co, 1, 2)) * 3
bl = Val(Mid(co, 3, 2)) * 4
For j = 1 To r Step 1
red = re - j * 2
green = gr - j * 2
blue = bl - j * 4
If red < 0 Then red = 0
If green < 0 Then green = 0
If blue < 0 Then blue = 0
col = RGB(red, green, blue)
Picture2.Circle (x + j / 3, y + j / 2), j, col
Next j
Next z
End Sub
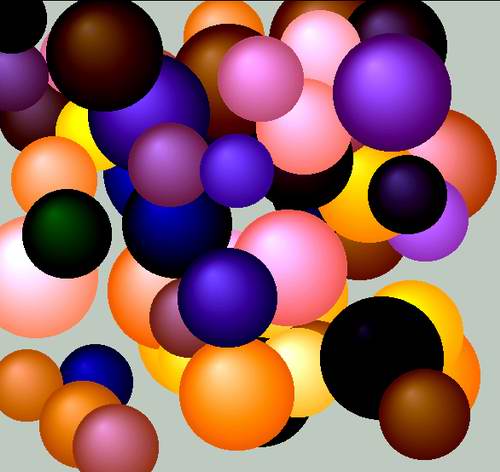
Рассмотрите полученный рисунок. Не смотря на
искусственность проделанных операций, он
волнует воображение – мы видим одно из
представлений таинственного числа. Покажите
знакомым – они будут удивлены открывающейся
красотой и многие, к своему удивлению,
заинтересуются числом Пи.
А мы пока движемся дальше по замеченным в Пи
чудесах. Если в магическом квадрате, у которого
сумма всех чисел в каждом ряду, каждом столбце и в
каждой диагонали равна 65, заменить
последовательно числа1, 2, 3… 25 соответствующими
цифрами числа Пи, то получим новый квадрат.
Исходный квадрат |
| 17 |
24 |
1 |
8 |
15 |
| 23 |
5 |
7 |
14 |
16 |
| 4 |
6 |
13 |
20 |
22 |
| 10 |
12 |
19 |
21 |
3 |
| 11 |
18 |
25 |
2 |
9 |
|
Квадрат из Пи |
| 2 |
4 |
3 |
6 |
9 |
| 6 |
5 |
2 |
7 |
3 |
| 1 |
9 |
9 |
4 |
2 |
| 3 |
8 |
8 |
6 |
4 |
| 5 |
3 |
3 |
1 |
5 |
|
Так вот – в новом
квадрате сумма чисел в первом столбце (17) равна
сумме чисел в пятом ряду, втором столбце (29) – в
четвертом ряду, в третьем столбце (25) – в третьем
же ряду, в четвертом столбце (24) – в первом ряду, и,
естественно (а точнее, очень даже удивительно), в
пятом столбце (23) - во втором ряду. Не правда ли
неожиданно? Не слишком ли много случайностей? –
Не сигнал ли это оккультной структуры? –
спрашивает Карлос Калвел из Лиссабона.
Это еще не все. Напомним формулу, предложенную
Джоном Матчином в 1706 году для вычисления Пи:
Pi = 16 * arctan (1/5) - 4 * arctan (1/239)
В ней снова видим старых знакомых – 5 и 239 (и 761, как
своего рода "фантом" ...).
Известно, также, что e^pi=23.1407. С другой стороны, мы
можем получить это значение с ошибкой всего в 0.0001
используя все те же числа 239 и 761:
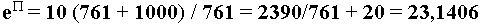
И еще - 239 и 23 - единственные числа, которые не
могут быть представлены суммой менее чем 9 кубов
чисел. Обратите внимание, что 239 = 10 x 23 + 9.
А сумма квадратов семи первых простых чисел
равна 666 (чур меня). При игре с этими числами можно
получить знакомца: 666/7 - 1/7 + 666 = 761. Но и 144
десятичных числа Пи дают в сумме 666 (не страшно?).
Мало того, 666 - 144 = 761 - 239 = 522 = 2 x 261. И, чтобы
покончить раз и навсегда с мистикой, напомним,
что 5761 год по древнееврейскому летоисчислению
наступил в сентябре 2000 года, и никаких концов
света, приходов мессий и прочих неприродных
явлений, напророченных к этой дате, не
наблюдалось. Но это вовсе не значит, что мы не
будем заниматься датами, ибо номер года содержит
в себе чудную задачу – выразить его (вы уже
догадались!) с помощью цифр числа Пи, используя
все математические действия. Нельзя лишь
нарушать порядок цифр.
Число
знаков |
Решение 2002 = |
20 |
3141 - 592 - 653 + 58
+ 9 + 7 + 9 + 32 + 3 - 8 - 4 |
13 |
31 x 41 + 592 + 6 x 5
x 3 + 5 x 8 + 9 |
11 |
314 x (1 + 5) + 92 + 6 + 5 x 3 + 5 |
10 |
314 x (1 + 5) + (9 + 2) x (6 + 5) - 3 |
9 |
31
x 41 + 5 + SQRT(9) - 2 + 6! + 5 |
8 |
((3
+ 1)! x 41 + 5 + 9) x 2 + 6 |
Попытайтесь улучшить,
используя меньше цифр, или, лучше займитесь годом
2003, присылайте варианты – это лучшее, что вы
можете сделать для человечества и заодно
обессмертить свое имя.
В течение двух тысячелетий волнует математиков
задача – с помощью циркуля и линейки построить
квадрат равновеликий (то есть с такой же
площадью) имеющемуся кругу, или, более известная
как «квадратура круга». Официальная математика
считает ее неразрешимой (наряду с не менее
известной задачи трисекции угла), еще в 1882
Линдеман доказал, что число Пи иррациональное, не
может быть корнем уравнения с рациональными
коэффициентами, и, следовательно, не может быть
построено классическими методами, то есть
циркулем и линейкой. Однако подобные ограничения
лишь раззадоривают энтузиастов, не оставляющих
надежду решить великую задачу и опрокинуть
устои. На приведенном рисунке построен отрезок
прямой, отличающийся от квадратного корня из Пи
всего на три миллионных доли процента.
Подразумевается, что отрезок, равный корню из
пяти вы умеете строить, это не очень сложно.
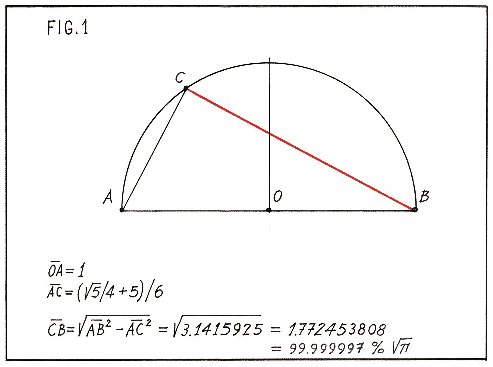
Попытайте счастья и вы, ведь прогресс двигают
именно те, кого не устраивают общеизвестные
ограничения и запреты.
А мы вернемся к нашим картинкам. Как еще, кроме
шаров, можно красиво представить
непредсказуемые цифры Пи? Думаем, думаем и – а
что, если рисовать не шары, а прямоугольники?
Попробовав разные варианты (откинув залитые
цветом и неправильные как не отвечающие нашим
представлениям о красоте) останавливаемся на
разноцветных квадратах. Алгоритм такой же, как и
с шарами, только вместо радиуса поучаем сторону
квадрата. Не хотелось бы навязывать оценку, но
уверен, что каждый найдет полученный коврик
красивым и даже веселым.

И фрагмент кода для квадратов:
Picture2.DrawWidth = 9
For z = 1 To 100 step 12
x = Val(Mid(c, z, 3)) / 2
y = Val(Mid(c, z + 3, 3)) / 2
r = Val(Mid(c, z + 6, 2)) + 0
co = Mid(c, z + 8, 4)
re = Int(Val(co) / 10)
gr = Val(Mid(co, 1, 2)) * 4
bl = Val(Mid(co, 3, 2)) * 5
For j = 1 To r Step 1
red = re - j * 2
green = gr - j * 2
blue = bl - j * 4
If red < 0 Then red = 0
If green < 0 Then green = 0
If blue < 0 Then blue = 0
col = RGB(red, green, blue)
Picture2.Line (x, y)-Step(r, r), col, B
Next j
Next z
И вдруг новая идея – выводить отрезки прямых
разной длины и под разным углом! Чтобы получить
длину и угол из тех же порций по 12 цифр выделяем
для координат по х и по y не по три цифры как для
шаров, а по две. Четыре, как и с шарами-квадратами
отдаем для цвета, а из оставшихся четырех два
используем для получения длины отрезка, а два –
для угла его наклона к горизонтальной оси, что,
впрочем, не так важно. И сразу же получаем
потрясающий рисунок, при некоторой фантазии в
нем можно даже разглядеть лохматое лицо, это и
есть один их портретов таинственного Пи.

И фрагмент кода.
Picture2.DrawWidth = 9
For z = 1 To 190
x = Val(Mid(c, z, 2)) * 3 + 100
y = Val(Mid(c, z + 2, 2)) * 3 + 50
r = Val(Mid(c, z + 4, 2)) * 2
u = 3.14159 * Val(Mid(c, z + 6, 2)) / 90
co = Mid(c, z + 8, 4)
re = Int(Val(co) / 10)
gr = Val(Mid(co, 1, 2)) * 6
bl = Val(Mid(co, 3, 2)) * 5
For j = 1 To r Step 1
red = re - j * 2
green = gr - j * 2
blue = bl - j * 4
If red < 0 Then red = 0
If green < 0 Then green = 0
If blue < 0 Then blue = 0
col = RGB(red, green, blue)
Picture2.Line (x, y)-Step(r * Cos(u), r * Sin(u)), col
Next j
Next z
Переменная u – и есть угол
наклона отрезков. Забавно, что, имея 720 знаков Пи,
мы все равно для перевода u в радианы взяли по
привычке 5 знаков, да и двух вполне хватило бы.
Надоело рисовать? На страничках http://www.math.ubc.ca/people/faculty/israel/bpi/bpi.html
и http://www.yfiles.com/pi.html
можете почитать о том, как в можно отыскать
значение числа Пи в библии. Но это для любителей
потусторонних тайн, а любителям настоящих тайн
реального мира предлагаем рассмотреть
удивительную эмпирическую формулу индийского
математика Раманужана (Ramanujan), предложенную им в
1910 году:
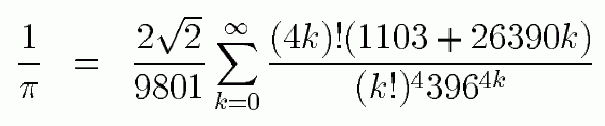
Каждый шаг итерации при использовании этого
алгоритма дает восемь правильных цифр в
разложении Пи, что позволило Госперу
(Gosper) в 1985 году получить 17 миллионов знаков числа
Пи.
Зачем же нам нужно знать столько много знаков
числа Пи? Ведь известно (мы писали уже об этом),
что для ошибки в несколько миллиметров при
полете на край нашей галактики (предположим, что
у нее есть край) достаточно всего 40 знаков. Кроме
того, что это вызов нашему интеллекту, попытка
проникнуть в тайны мироздания, есть и
практические аспекты головокружительного
уточнения Пи. Во-первых, проверка
работоспособности нового оборудования. Ходят
легенды о том, что именно эта задача позволила в
1986 году найти ошибку в создаваемом
суперкомпьютере Cray-2. Кроме того, математикам
нужны значения чисел Пи, е, 20.5, 100.5 и другие
константы. Они используются при вычислениях
сходящихся рядов, для получения псевдослучайных
чисел и в других приложениях математики.
Еще одно невероятное свойство числа Пи – его
связь с числами Фибоначчи найдете на http://www.mcs.surrey.ac.uk/Personal/R.Knott/Fibonacci/fibpi.html
.Авторы с помощью геометрических построений
(причем, элементарных!) доказывают, что
arctan(1) = arctan(1/2) + arctan(1/3)
arctan(1/3) = arctan(1/5) + arctan(1/8)
arctan(1/8) = arctan(1/13) + arctan(1/21)
arctan(1/21) = arctan(1/34) + arctan(1/55)
И так далее. Ну и что? – спросите вы. Дело в том,
arctan(1)=Пи/4. Поэтому, сначала заменим arctan (1/3) в
первой строке
Pi/4 = arctan(1)
= arctan(1/2) + arctan(1/3)
= arctan(1/2) + arctan(1/5) + arctan(1/8)
а потом подставим выражение вместо arctan(1/8):
Pi/4 = arctan(1/2) + arctan(1/5) + arctan(1/13) + arctan(1/21)
Продолжая процесс мы заметим, что у нас участвуют
числа Фибоначчи
Pi/4 = arctan(1)
= arctan(1/2) + arctan(1/3)
= arctan(1/2) + arctan(1/5) + arctan(1/8)
= arctan(1/2) + arctan(1/5) + arctan(1/13) + arctan(1/21)
= arctan(1/2) + arctan(1/5) + arctan(1/13) + arctan(1/34) + arctan(55)
=...
Но не все, а только те, которые стоят на нечетных
местах, то есть, имеют нечетный порядковый номер.
Pi/4 = arctan(1/F1 )
= arctan(1/F3) + arctan(1/(F4)
= arctan(1/F3) + arctan(1/F5) + arctan(1/F6)
= arctan(1/F3) + arctan(1/F5) + arctan(1/F7) + arctan(1/F8)
= arctan(1/F3) + arctan(1/F5) + arctan(1/F7) + arctan(1/F9) + arctan(1/F10)
= ...
А каждый последний четный член мы сможем
заменить на сумму арктангенсов обратных величин
нечетного и четного, который в свою очередь… и
так далее. Не правда ли неожиданное проявление
знакомого казалось бы до конца числа Пи?
И еще забавные сведения о Пи, полученные на http://www.jvshly.de/piworld/apple_pi.htm . Двадцать второго июля (день
приближенного Пи, напоминаю, а День Пи 14 марта, не
пропустите!) 2000 года в Хохенчоенхаузене под
Берлином (Berlin-Hohenschoenhausen ) прохожие могли стать
свидетелями необычного действия. Максвелл Демон
из 1392 яблок выложил на траве первые 314 цифр
волшебного числа.




И, все-таки, еще один рисунок.
Теперь в старичке Turbo Pascal’e. Оцените идею – в
каждом квадратике на фоне зеленого фона рисуем
белый прямоугольник шириной пропорциональной
цифре числа Пи. От тоненькой полоски для единицы
до полного квадрата для девяти.

Не оценить красоту полученной
картинки может только совсем скучный и
обделенный фантазией обыватель. Попробуйте
поменять цвет фона, цвет заливки и толщину швов
(переменная s), каждая картинка будет по-своему
красива.
PROGRAM virus;
USES CRT,GRAPH,DOS;
VAR
M,S,X,Y,X0,Y0,I,J : INTEGER;
Q,P : ARRAY [1..10,1..10] OF integer ;
PI,PI1,CH1: STRING;
GraphDriver,GraphMode:INTEGER ;
Procedure Ris ;
begin
end;
{+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++}
BEGIN
PI:='3141592653589793238462643383279
50288419716939937510582097494459230
78164062862089988628034825342117067';
GraphDriver:= Detect;
InitGraph(GraphDriver,GraphMode,'');
SETLINESTYLE(0,0,1);
SETFILLSTYLE(1,0) ;
BAR(0,0,640,480) ;
SETFILLSTYLE(1,2) ;
Y:=40 ; M:=30 ; S:=3 ; i:=1 ; j:=1 ;
REPEAT
X:=120 ; I:=1;
REPEAT
SETFILLSTYLE(1,2) ;
BAR(X,Y,X+M,Y+M) ;
SETFILLSTYLE(1,15);
PI1:=COPY(PI,((J-1)*10+I),1);
VAL(PI1,Q[j,i],T);
BAR(X,Y,(X+3*Q[J,I]),Y+M);
X:=X+M+S; i:=i+1 ;
UNTIL I>10 ;
Y:=Y+M+S ; j:=j+1 ;
UNTIL J>10 ;
ch1:=readkey;
end.
Напоследок – интересные
сведения о рекордсменах по запоминанию числа Пи.
Вот что говорит рекордсмен мира по запоминанию
числа Пи Хидеаки Томойори
(его рекорд 40000 знаков): «Конечно, мне не удалось
бы запоминать такое огромное, иррациональное
число простой зубрежкой. Вместо этого я разбил
его на короткие последовательности по десять
цифр в каждой. Затем я проассоциировал звук
каждого числа с конкретным словом. А из слов уже
образовал предложения, которые смог запомнить
как конкретные образы. Так, для каждой группы
десяти цифр, я сначала придумываю ключевое слово,
таким образом, что это ключевое слово напоминает
мне образ и все предложение, а затем уже звуки
этого предложения напоминают мне точную
последовательность чисел.»
Рамеш Махадеван, запомнивший 30000 знаков Пи: «Я
получил многие свои знания от Ведической
математики, я могу показать вам книги, которые
использую. Поэмы на санскрите очень интересны.
Одно и то же стихотворение можно
интерпретировать как восхваление Шивы и Кришны и
одновременно как математическую формулу. Там
есть приближение Пи до тридцать восьмого знака.
Есть решение квадратного уравнения. Сейчас нашли
там знания на уровне высшей школы в Индии.»
Цитированные и другие интересные рассказы о
чудо-запоминателях (и не только) расположены на
страничке рекордсмена мира по запоминанию Олега
Степанова http://users.lk.net/~stepanov или на его "арбузном
филиале"
|