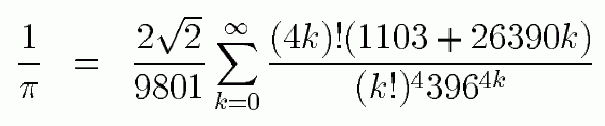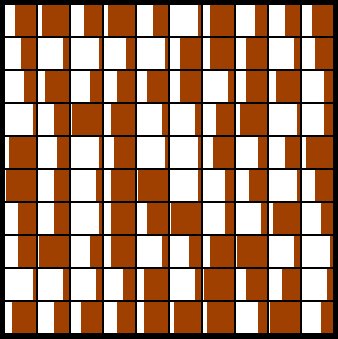Пи-клуб, питомник пижонов.
Опубликовано в Компьютерре №17(492) 2003
– В последующие дни я экспериментировал
с растениями,
птицами и рыбами, нанизывал спирали ДНК, составлял
Периодическую систему, изобретал законы согласования
и число "пи". Знаете, чего стоит изобрести число "пи"?
http://www.rg-rb.de/ch&k/2000/30/05.shtml
На круглых дураков число Пи не распространяется.
В. Шендерович.
Большинство из нас будут удивлены, узнав, что многие люди занимаются числом Пи – ведь в школе на нелюбимой многими геометрии уяснили, что это отношение длины окружности к диаметру, что тут может быть еще интересного? Но, познакомившись поближе с этим виртуальным героем, мы будем удивлены еще больше, ибо история человечества предстанет нам как интригующая череда усилий величайших умов по уточнению знаков числа Пи и поисков алгоритмов для этого. Знакомство с загадочным числом предлагаем проводить в виде прогулок по виртуальному клубу, посвященному Пи. Что же это за клуб такой? Самый настоящий Пи-клуб (не путать с Пиквикским и клубом любителей пива, хотя членство в них допускается). Кто же является членом самого престижного клуба. Во-первых, конечно, все Петры Ильичи, Пал Иванычи, Пулаты Ибрагимовичи и Пелагеи Иннокентьевны плюс Пироговы, Пилюлькины, Пинхасовы и Писаренки плюс любители пикников с пирожными и пирожков с пивом – они зачисляются автоматически. Так же как и пианисты, пилигримы, писатели и прочие пигмеи, вопрос о пионерах и пиратах пока не решен. Ну и конечно все, кто хоть раз проводил окружность и задумался о таинственном и непредсказуемом числе Пи.
В первом зале, естественно, само число Пи. Рассмотрите внимательно, его первую тысячу знаков, проникнитесь поэзией этих цифр, ведь за ними стоят тени величайших мыслителей Древнего мира и Средневековья, Нового и настоящего времени, Египта, Греции и Китая.
Пи = 3.
1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679 8214808651 3282306647 0938446095 5058223172 5359408128 4811174502 8410270193 8521105559 6446229489 5493038196 4428810975 6659334461 2847564823 3786783165 2712019091 4564856692 3460348610 4543266482 1339360726 0249141273 7245870066 0631558817 4881520920 9628292540 9171536436 7892590360 0113305305 4882046652 1384146951 9415116094 3305727036 5759591953 0921861173 8193261179 3105118548 0744623799 6274956735 1885752724 8912279381 8301194912 9833673362 4406566430 8602139494 6395224737 1907021798 6094370277 0539217176 2931767523 8467481846 7669405132 0005681271 4526356082 7785771342 7577896091 7363717872 1468440901 2249534301 4654958537 1050792279 6892589235 4201995611 2129021960 8640344181 5981362977 4771309960 5187072113 4999999837 2978049951 0597317328 1609631859 5024459455 3469083026 4252230825 3344685035 2619311881 7101000313 7838752886 5875332083 8142061717 7669147303 5982534904 2875546873 1159562863 8823537875 9375195778 1857780532 1712268066 1300192787 6611195909 2164201989
Зачем, спросит обыватель, нам столько много знаков Пи, ведь известно, что для расчета полета на край нашей Галактики с точностью, равной диаметру протона, достаточно знать 40 знаков числа, а при расчете Земной орбиты вокруг Солнца с точностью до миллиметра достаточно 14 знаков? А уже в XVII веке были получены первые 34 знака. Трудно будет объяснить деловым людям, ожидающим непременную сиюминутную выгоду от каждого движения, что число Пи, как и простые числа, совершенные, дружественные, числа Мерсена – это вызов нашему интеллекту, волнующая загадка устройства мира и просто интересно. (Простые числа в последнее время пользуются вниманием практиков, так как на их основе генерируются криптопротоколы для защиты информации.)
Какое бы сочетание цифр мы бы не выдумали – оно непременно встретится в знаках числа Пи, то есть можно ожидать появление любой наперед заданной последовательности цифр. Например, самые распространенные расстановки встретились в следующих по счету цифрах:
01234567891 : с 26,852,899,245
01234567891 : с 41,952,536,161
01234567891 : с 99,972,955,571
01234567891 : с 102,081,851,717
01234567891 : с 171,257,652,369
01234567890 : с 53,217,681,704
01234567890 : с 148,425,641,592
27182818284 : с 45,111,908,393 – это цифры числа е. (Была такая шутка: ученые нашли последнее число в записи Пи – им оказалось число е, почти попали)
Попробуйте поискать в первых десяти тысячах знаков Пи свой телефон или дату рождения, если не получится, то ищите в 100.000 знаков.
И еще – в числе 1/Пи начиная с 55,172,085,586 знака идут 3333333333333, не правда ли удивительно?
Да что ходить далеко – даже в первой тысяче есть неожиданности - пять девяток подряд.
Есть гипотезы, предполагающие, что в числе Пи скрыта любая информация, которая когда-либо была или будет доступна людям. В том числе и различные предсказания – надо только их найти и расшифровать, имея под рукой компьютер это не составит большого труда. Хочется только напомнить, что один исследователь, в ответ на сообщения о наличии в Библии зашифрованных предсказаний, сообщил, что он с помощью программы нашел в Библии предсказание о том, что в ней нет никаких предсказаний. Но это вовсе не значит, что мы должны прекратить наши опыты с Пи.
В следующем зале, естественно, история открытия и уточнения числа Пи. В нем можно ознакомиться с интригующими подробностями уточнения Пи, начиная от 16/9=3,1604 у египтян, 22/7 =3.1428 у греков, =3.162 у индусов, 355/113=3.14159 у китайцев, и до астрономической точности нашего времени.
Обозначение числа Пи происходит от греческого слова perijerio ("окружность"). Впервые это обозначение использовал в 1706 году английский математик У.Джонс, но общепринятым оно стало после того, как его (начиная с 1736 года) стал систематически употреблять Леонард Эйлер. В конце XVIII века И.Ламберт и А.Лежандр установили, что
Пи иррациональное число, а в 1882 году Ф.Лидерман доказал, что оно трансцендентное, т.е. не может удовлетворять никакому алгебраическому уравнению с целыми коэффициентами.
На протяжении всего существования числа Пи , вплоть до наших дней, велась своеобразная "погоня" за десятичными знаками числа
Пи. Леонардо Фибоначчи около 1220 года определил три первых точных десятичных знаков числа Пи. В XVI веке Андриан Антонис определил 6 таких знаков. Франсуа Виет (подобно Архимеду), вычисляя периметры вписанного и описанного 322216-угольников, получил 9 точных десятичных знаков. Андриан Ван Ромен таким же способом получил 15 десятичных знаков, вычисляя периметры 1073741824-угольников. Лудольф Ван Кёлен, вычисляя периметры 32512254720-угольников, получил 20 точных десятичных знаков. Авраам Шарп получил 72 точных десятичных знаков числа Пи. В 1844 году З.Дазе вычисляет 200 знаков после запятой числа Пи, в 1847 году Т.Клаузен получает 248 знаков, в1853 Рихтер вычисляет 330 знаков, в том же 1853 году 440 знаков получает З.Дазе и в этом же году У.Шенкс получает 513 знаков.
С появлением компьютеров темпы возросли:
1949 год- 2037 десятичных знаков (Джон фон Нейман, ENIAC),
1958 год- 10000 десятичных знаков (Ф.Женюи, IBM-704),
1961 год- 100000 десятичных знаков (Д.Шенкс, IBM-7090),
1973 год- 10000000 десятичных знаков (Ж.Гийу, М.Буйе, CDC-7600),
1986 год- 29360000 десятичных знаков (Д.Бейли, Cray-2),
1987 год- 134217000 десятичных знаков (Т.Канада, NEC SX2),
1989 год- 1011196691 десятичных знаков (Д.Чудновски и Г.Чудновски, Cray-2+IBM-3040)
Они же добились в 1991 году 2260000000 знаков, а в 1994 году - 4044000000 знаков.
Дальнейшие рекорды принадлежат японцу Тамуре Канада: в 1995 году 4294967286 знаков, в 1997 – 51539600000, и, последний на сегодня рекорд 206.158.430.000 знаков. Суперкомпьютер (проект HINTS - High-performance Numerical Tools & Software для сверхмощных научных и инженерных вычислений
http://www.hints.org/HINTSw.html
) в сентябре 1999 года работал 37 часов 21 минуту 4 секунды используя 865 Гигабайт памяти для основной задачи и 46 часов, 816 Гигабайт для вспомогательной оптимизации вычислений.
Следующий зал посвящен методам вычислений Пи. Начиная с Архимеда математики вписывали в круг правильный многоугольник и находили отношение периметра к радиусу. Например, в первой половине XV в. в обсерватории Улугбека, возле Самарканда, астроном и математик ал-Каши вычислил число "пи" с 16 десятичными знаками. Он сделал 27 удвоений числа сторон многоугольников и дошел до многоугольника, имеющего 3*228 углов. Спустя полтора столетия в Европе Ф.Виет нашел число "пи" только с 9 правильными десятичными знаками, сделав 16 удвоений числа сторон многоугольников. Но при этом Ф.Виет первым заметил, что число "пи" можно отыскать, используя пределы некоторых рядов. Это открытие имело огромное значение, так как позволило вычислять Пи с какой угодно точностью. Однако только через 250 лет после ал-Каши его результат был превзойден.
Так Г.Лейбниц получил в 1674г. ряд
Пи/4=1-1/3+1/5-1/7+1/9-1/11…
Не поленитесь – накидайте программу, просуммируйте ряд и проверьте
Пи . Или по формуле, связывающей сторону многоугольника с удвоенным числом сторон со стороной исходного многоугольника, уточняя отношение периметра к диаметру.
В Сети много страниц, посвященных вычислению Пи, отметим лишь, что на
http://www.cs.unb.ca/~alopez-o/math-faq/mathtext/node12.html
расположена программа, написанная Диком Т. Винтером (Dik T. Winter at CWI) на Си всего 160-ю символами, но вычисляющая 800 знаков Пи!
int a=10000,b,c=2800,d,e,f[2801],g;main(){for(;b-c;)f[b++]=a/5;
for(;d=0,g=c*2;c-=14,printf("%.4d",e+d/a),e=d%a)for(b=c;d+=f[b]*a,
f[b]=d%--g,d/=g--,--b;d*=b);}
На этом общеознакомительная часть знакомства с Пи, вероятно известная уже любителям математики, заканчивается, и начинаются изысканные угощения для настоящих ценителей.
К известным методам уточнения Пи (подбором деления пар чисел, вписывания в круг многоугольника и вычисления сумм рядов) во второй половине ушедшего века добавились еще три, которые можно назвать экспериментальными. Первый, так называемый "метод иглы Бюффона". В нем на разлинованную равноудаленными прямыми плоскость произвольно бросается игла, длина которой равна половине расстояния между соседними прямыми. (Так что игла либо не пересекает прямые, либо пересекает ровно одну при каждом бросании). Можно доказать, что отношение числа пересечений иглы с какой-нибудь линией к общему числу бросаний стремится к Пи при увеличении числа бросаний до бесконечности. Нужно сделать очень много испытаний, чтобы получить более-менее приличную точность приближения полученной дроби к Пи, а кроме того, при эксперименте надо внимательно следить, чтобы бросание иглы было "равновероятным": метод иглы Бюффона существенным образом базируется на методах теории вероятностей. Из уважения к читателям и чтобы не лишать их прекрасных мгновений творчества приводить текст программы не будем. Неужели не таинство – бросаем на экране случайным образом ориентированный отрезок, проверяем – не пересек ли горизонтальные линии, все это в цикле, накапливаем статистику и убеждаемся (или не убеждаемся) в правильности общеизвестных цифр любимого числа. На экран можно и не выводить для скорости, но вид случайно рассыпанных иголок красив сам по себе.
Второй метод, придуманный Г.А. Гальпериным, и называемый Пи-биллиардом, основан на оригинальной модели. При столкновении двух шаров, меньший из которых находится между большим и стенкой, и больший движется к стенке, число соударений шаров позволяет вычислить Пи со сколь угодно большой наперед заданной точностью. Надо только запустить процесс (можно и на компьютере) и посчитать число ударов шаров. Подробное описание метода с обоснованием его смотрите на
http://phys.web.ru/db/msg.html?mid=1161679&uri=pi.html
Для третьего метода можно воспользуемся известным предположением теории чисел: вероятность, что два числа взаимно просты равна 6/ Пи 2
Взаимно простыми называются числа, не имеющие общих делителей (для строгости обычно добавляют “кроме единицы”). Какой же алгоритм наших действий? Берем два случайных числа, находим их делители и сравниваем их. Повторяя процесс в цикле, вычисляем долю шагов цикла (от общего числа шагов), при которых числа не имели общих делителей. Разделив 6 на эту долю и извлеча (есть такое слово?) квадратный корень из частного, получим искомое значение
Пи .
К новым экзотическим методам относится и эмпирическая формула индийского математика Раманужана (Ramanujan), предложенная им в 1910 году:
Каждый шаг итерации при использовании этого алгоритма дает восемь правильных цифр в разложении
Пи , что позволило Госперу (Gosper) в 1985 году получить 17 миллионов знаков
Пи .
Для тех, кто испытывает наслаждение от прикосновения к клавиатуре есть красивая, этюдная задача – найти два наибольших числа, дающих при делении друг на друга наилучшее приближение к ?. Решая задачу «в лоб» можно найти, что частное от деления 5 419 351 на 1 725 033 отличается от известного значения ? всего на 2,53130849614536*10-14 и это предел машинного представления чисел с двойной точностью - тип double в Visual Basic. Мой знакомый, используя головоломные ухищрения, обошел эти ограничения и нашел, что 411 557 987 деленное на 131 002 976 дает 17 правильных знаков
Пи . Кто следующий?
Устали? Отвлечемся от вычислений. И подумаем, как легче запомнить значение Пи? Это можно сделать, например, с помощью старинного двустишья. Оно написано по правилам старой русской орфографии, по которой после согласной в конце слова обязательно ставился "мягкий" или "твердый" знак. Вот оно, это двустишие:
Кто и шутя, и скоро пожелаетъ
"Пи" узнать число - ужъ знаетъ.
Количество букв в каждом слове равно соответствующей цифре числа Пи, проверьте! Первую тройку, естественно, отделите точкой.
А почему, собственно, мы должны пользоваться дореволюционными стихами? Известна также фраза «это я знаю и помню прекрасно», но хотелось бы побольше знаков (вдруг придется лететь через Галактику) и с рифмой. Ведь это же не сложно, написать такое стихотворение! Займитесь на досуге и присылайте, ваши шедевры будут размещены в клубе, прославитесь.
А вот (http://www.go2net.com/useless/useless/pi.html) варианты на английском: "How I want a drink, alcoholic of course, after the heavy lectures involving quantum mechanics!", перевод, правда, в педагогических целях лучше не приводить. И еще:
Now
I even I
Would celebrate
In rhymes unapt
The great immortal Syracusan
Rivaled nevermore
Who in his wondrous lore
Passed on before
Gave men his guidance
How to circles mensurate
А вот созвучное ему (тоже про Сиракузы речь идет) стихотворение С. Боброва не мнемоническое, но тоже с запоминанием цифр числа Пи:
Про число "ПИ" - 3,1415926
Гордый Рим трубил победу
Над твердыней Сиракуз;
Но трудами Архимеда
Много больше я горжусь.
Надо нынче нам заняться,
Оказать старинке честь,
Чтобы нам не ошибаться,
Чтоб окружность верно счесть,
Надо только постараться
И запомнить все как есть
Три — четырнадцать —
пятнадцать — девяносто два и шесть!
Это стихотворение перекликается с цифровыми стихами, подробнее смотрите альманах
Полторы трубы
И еще стихотворение с присутствием Пи, наверняка известное читателям, из Алисы в переводе Б. Заходера:
Математик и Козлик
Делили пирог.
Козлик скромно сказал:
- Раздели его вдоль!
- Тривиально! - сказал Математик.
- Позволь,
Я уж лучше
Его разделю поперек!
- Первым он ухватил
Первый кус пирога.
Но не плачьте,
Был тут же наказан порок:
"Пи" досталось ему
(А какой в этом прок?!)
А Козленку...
Козленку достались
Рога!
Лежит этот стишок на
http://www.weekend.ru/print.cfm?publication=4444
, прекрасной странице, посвященной Пи. На ней мы узнаем, например, что на
http://www.hut.fi/~mnippula/votepi.html
проводилось голосование на тему: чему должно быть равно число Пи в будущем? Большинством голосом решено, что Пи=42. Вот так полагаться на большинство.
Очаровательная Ева Андерссон из Калифорнии, девушка с зеленым лицом и рожками-антенами (у многих ли хватит смелости и чувства юмора выложить себя в таком виде, смотрите
http://www.ugcs.caltech.edu/~eveander/index.html
) разработала викторину, посвященную числу Пи. Если вы не сможете
ответить на 25 тестов, то получите познавательные ответы на них. А вот что
говорит рекордсмен мира по запоминанию числа Пи Хидеаки Томойори
(его рекорд 40000 знаков): «Конечно, мне не удалось бы запоминать такое огромное, иррациональное число простой зубрежкой. Вместо этого я разбил его на короткие последовательности по десять цифр в каждой. Затем я проассоциировал звук каждого числа с конкретным словом. А из слов уже образовал предложения, которые смог запомнить как конкретные образы. Так, для каждой группы десяти цифр, я сначала придумываю ключевое слово, таким образом, что это ключевое слово напоминает мне образ и все предложение, а затем уже звуки этого предложения напоминают мне точную последовательность чисел.»
Рамеш Махадеван, запомнивший 30000 знаков Пи : «Я получил многие свои знания от Ведической математики, я могу показать вам книги, которые использую. Поэмы на санскрите очень интересны. Одно и то же стихотворение можно интерпретировать как восхваление Шивы и Кришны и одновременно как математическую формулу. Там есть приближение
Пи до тридцать восьмого знака. Есть решение квадратного уравнения. Сейчас нашли там знания на уровне высшей школы в Индии.»
Надеюсь, отдохнули – возвращаемся к цифрам ?. Если вдруг возникнет подозрение, что какие-то цифры в разложении
Пи встречаются чаще, а какие-то реже, то имейте в виду, что в первых 200,000,000,000 десятичных знаках
Пи цифры встречались с такой частотой:
'0' : 20000030841;
'1' : 19999914711;
'2' : 20000136978;
'3' : 20000069393
'4' : 19999921691;
'5' : 19999917053;
'6' : 19999881515;
'7' : 19999967594
'8' : 20000291044;
'9' : 19999869180;
Поразмышляйте об этом.
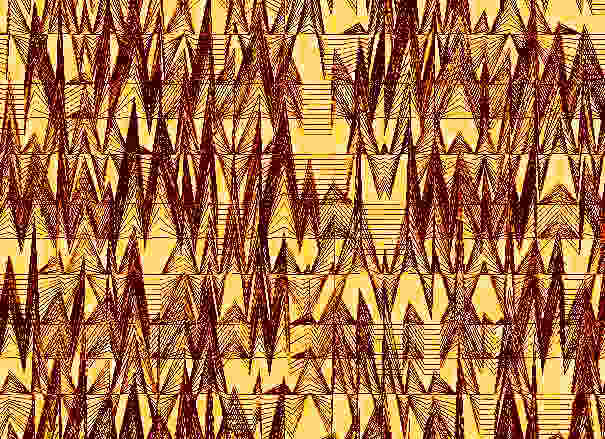
В каждом зале клуба на стенах висят невероятные картины. Например, полученная со страницы
http://www.algonet.se/~eliasb/pi/binpi.html
, посвященной представлению цифр числа Пи в двоичной форме.

Рассмотрите ее, попытайтесь увидеть, что в ней зашифровано природой.
А эта картина получена движением точки в зависимости от символа двоичного числа – 1 – поворот направо, 0 – налево.

На замечательной странице http://www.jvshly.de/piworld
много чудес, связанных с Пи , например, такие его представления

А что же мы? - вопрошал любимый поэт, - и мы не хуже многих. За несколько минут в безотказном старичке Turbo Pascal’e набросаем небольшой шедевр – ширина белых участков в каждом квадратике пропорциональна соответствующему числу из разложения нашего героя.
Только недобрый человек или вконец измученный хлопотами сисадмин не увидят в этом коврике что-то волнующе красивое.
Перед завершением осмотра три изюминки.
Первая в виде предостережения: в Индиане (штат США) в соответствии с законом число "пи" равно 4, а не 3,1415. Подробности на
http://smith.lvivnet.com/article.php?aid=1076
Вторая – как выразить текущий год цифрами Пи используя все математические действия.
| Число знаков |
Решение 2002 = |
| 20 |
3141 - 592 - 653 + 58 + 9 + 7 + 9 + 32 + 3 - 8 - 4 |
| 13 |
31 x 41 + 592 + 6 x 5 x 3 + 5 x 8 + 9 |
| 11 |
314 x (1 + 5) + 92 + 6 + 5 x 3 + 5 |
| 10 |
314 x (1 + 5) + (9 + 2) x (6 + 5) - 3 |
| 9 |
31 x 41 + 5 + SQRT(9) - 2 + 6! + 5 |
| 8 |
((3 + 1)! x 41 + 5 + 9) x 2 + 6
|
Попытайтесь улучшить, используя меньше цифр, и пора уже приглядываться к цифре 2003, присылайте варианты – это лучшее, что вы можете сделать для человечества.
Третья – знаете ли вы, какой праздник самый естественный, самый настоящий, не связанный с религиями, национальными, историческими политическими и прочими суетными делами? Это, конечно, день числа
Пи , объединяющий всех людей, всех мыслящих существ Галактики и Вселенной, 14 марта (3.14 в американской нотации, неизвестно, правда, как выглядит этот день в календарях других цивилизаций, но не стоит придираться - договоримся), не пропустите.
Ну вот и все. Присоединяйтесь. Для тех, кто пропустил день Пи, есть еще день приближенного Пи, естественно, 22 июля. Не прозевайте.
Осталась только закрытая комната с ненормативной лексикой, основанной на числе Пи. Поэтому, кстати, пираты и пионеры, злоупотребляющие ею, в клуб не принимаются.
Сам клуб, десять тысяч, сто тысяч знаков Пи , статьи с алгоритмами и результатами вычисления
Пи , многочисленные занимательные сведения о нем и
ссылки на ресурсы Сети найдете в нашем
клубе Пи. Цитированные и другие интересные рассказы о чудо-запоминателях (и не только) расположены на
страничке рекордсмена мира по запоминанию Олега
Степанова http://users.lk.net/~stepanov или на его "арбузном
филиале"
|