Опубликовано в журнале Hard'n'Soft №8 2003 (стр 114) в сокращении под названием "Плещут холодные волны"

Водяные опыты юных физиков

Не нужна мне с неба манна
Мне бы только ванна, ванна...

Если вы, купаясь в ванне, не проводите эксперименты, то вы пропащий человек, и время в ванне расходуете впустую, о чем, как известно, писал, бросая в воду камушки, Козьма Прутков и кричал любитель купания Архимед. По количеству и занимательности всевозможных опытов купание в ванне соперничает с компьютерными забавами, а попытка их объединить доставит нам не мало приятных минут.

Часть 1, кафельная

Пока набирается вода, посмотрите на стены и на пол, обычно выложенные кафелем. Если вам повезло и в вашей кладке ряды смещены, то вы увидите замечательный эффект - ряды кафеля не параллельны! "Иллюзия кафельной стенки" возникает при разглядывании плоскости, покрытой чередующимися квадратами или прямоугольниками, которые разделены тонкими "швами". Иллюзия состоит в том, что горизонтальные линии кажутся сходящимися к левой или правой стороне.


Направление схождения меняется от ряда к ряду: в одном ряду плитки как бы увеличиваются слева направо, в другом - справа налево. Специалисты по зрительному восприятию обратили внимание на эту иллюзию в начале 1970-х годов, после того, как она была замечена на стенке кафе в Бристоле, в Великобритании. Р. Грегори и П. Херд из Бристольского университета опубликовали первый подробный анализ этой иллюзии. Они связали её с гораздо более старой иллюзией, известной под названием узора Мюнстерберга и названной так по имени психолога Х. Мюнстерберга, описавшего её в 1897 году. В узоре Мюнстерберга верхняя и нижняя стороны каждой плитки кажутся наклонными и направление наклона меняется от ряда к ряду. Однако эффект схождения здесь слабее. Грегори, Херд и другие исследователи заметили, что иллюзия кафельной стенки проявляется особенно отчётливо, когда тёмные и светлые плитки контрастируют по яркости, а шов достаточно узок и по яркости занимает промежуточное положение между тёмными и светлыми плитками. Если яркость шва такая же, как у светлых плиток, иллюзия ослабевает и даже может совсем пропасть, если же шов совсем светлый, иллюзии не возникает вообще. Когда шов такой же тёмный, как и тёмные плитки, возникает иллюзия Мюнстерберга со слабым схождением; если он более тёмный, схождение отсутствует. Плитки не обязательно должны быть чёрными и белыми, они могут быть цветными, но если они не различаются по яркости, иллюзии не возникает. Плитки должны чередоваться в строгом порядке. Однако, если они смещены так, что образуют в точности шахматную доску, иллюзия так же отсутствует. Убедиться в этом можно рассматривая анимированную картинку, в ней ряды через один все время смещаются, рисуя то вертикальные полосы, то шахматную доску. В промежуточных положениях возникает иллюзия не параллельности рядов. Потом, при движении рядов, иллюзия пропадает и возникает снова с кажущимися наклонами уже в другую сторону. Вопрос для дотошных исследователей - будет ли иллюзия не параллельности при вертикальном сдвиге четных столбцов относительно нечетных?
Для дальнейших опытов, учитывая важность темы, предлагаем набрать приведённую ниже программу в Turbo Pascal'e и понаблюдать на экране иллюзию кафельной стенки:

PROGRAM KAFEL USES CRT,GRAPH,DOS; VAR M,S,X,Y : INTEGER; C: STRING; procedure GrInit; var GraphDriver : Integer; GraphMode : Integer; ErrorCode : Integer; begin GraphDriver:= Detect; InitGraph(GraphDriver,GraphMode,''); ErrorCode:=GraphResult; if ErrorCode grOk then begin Writeln('Ошибка графики',GraphErrorMsg(ErrorCode)); Writeln('Программа остановлена'); Halt (1) end {if} end; {+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++} BEGIN GRINIT; SETFILLSTYLE(1,0) ; {1} BAR(0,0,640,480) ; SETFILLSTYLE(1,15) ; {2} Y:=0 ; M:=40 ; S:=2 ; {3} REPEAT X:=0 ; REPEAT BAR(X,Y,X+M,Y+M) ; SETCOLOR(0) ; LINE(0,Y,640,Y) ; {4} X:=X+M+M+S; UNTIL X > 640 ; Y:=Y+M+S ; X:=M DIV 2 ; {5} REPEAT BAR(X,Y,X+M,Y+M) ; SETCOLOR(0) ; LINE(0,Y,640,Y) ; {6} X:=X+M+M+S; UNTIL X > 640 ; Y:=Y+M+S ; UNTIL Y>480 ; C:=READKEY ; CLOSEGRAPH; END.

В программе можно поменять цвета темных и светлых плиток в строках 1 (заливка фона) и 2 (заливка выводимых в цикле квадратиков), можно, так же, менять размер плиток и ширину шва - переменные M и S в строке 3 . Попробуйте разные варианты сочетаний цветов плиток, посмотрите, как меняется иллюзия искривления. Ещё можно понаблюдать эффекты от прочерчивания или удаления линий (подбирая их цвет) на швах, удалив или сохранив строки 4 и 6, и от попытки изменить сдвиг между рядами в строке 5. Попробуйте, и вы будете вознаграждены удивительными эффектами. И если вам придётся выбирать рисунок при укладке настоящего кафеля, то вы уже наверняка сможете удивить своих гостей иллюзией искривления, это круче, чем держать в ванне крокодила, ибо необъяснимо. Иллюзия возникает из-за особенностей устройства фоторецепторов на сетчатке глаза. Хотя известно, что мы видим не столько глазами, сколько мозгом - он обрабатывает поступившие сигналы в соответствии с опытом, приобретенным или унаследованным.

Похожие эффекты часто встречаются на хорошо известных любителям математики изображениях, когда параллельные линии кажутся не параллельными, а концентрические окружности кажутся спиралями.


Часть 2, кристаллическая

Я же про этот шторм и шквал
Ведать не ведал, знать не знал.
Я в это время по Фонтанке
В белой рубашечке гулял.
М. Щербаков

Коснитесь двумя пальцами поверхности воды, повибрируйте ими и вы увидите картину совмещения или интерференции волн от двух источников. Меняя расстояние между пальцами, фазы колебаний пальцев и наблюдая за тенью водной поверхности на дне ванны, вы откроете для себя много нового.
Если спросить читателя - любите ли вы кристаллографию, то ответ будет наверняка отрицательным. С какой стати ее любить? То ли дело физика со сказочными уравнениями де Бройля и черными дырами, химия, если вам повезло в школе с учителем, биология с таинственными генетикой и дарвинизмом, математика, пронизанная логикой и совершенством. И хотя не обходили кристаллографию вниманием популярные журналы и почти все знают, что в 1892 году Федоров и Шанфлис рассмотрели все 230 возможных вариантов симметричных кристаллов, что в 1912 году Лауэ открыл дифракцию рентгеновских лучей на кристаллах, а в 70-х годах Пенроуз предложил модель непериодического замощения плоскости и все наслышаны о фотонных кристаллах и расшифровке пространственного расположения молекулы гемоглобина, но, тем не менее, в сознании обывателя кристаллография представляется узкоспециальной скушноватой наукой типа агрохимии или техники безопасности в литейном производстве.
Но эта самая кристаллография натолкнула на забавную идею и позволила испытать приятные минуты, когда пролистывая очередное сообщение о дифракционных методах исследования кристаллов, я вдруг подумал, а ведь дифракцию можно смоделировать на компьютере безо всяких кристаллов! И, чтобы растянуть удовольствие, точнее, предвкушая его, я не бросился сразу к клавиатуре, а несколько дней любовался очередной находкой, обдумывал варианты исполнения. Физическая модель проста - в непрозрачной стенке имеются маленькие отверстия, которые, согласно принципу Гюйгенса, становятся самостоятельными источниками света. На некотором расстоянии от стенки располагается экран, на котором волны, пришедшие от разных источников должны нарисовать некоторую картину. В каждой точке экрана освещенность определяется сложением волн от каждого отверстия с учетом фазы, в которой волна достигает экран. То есть волны одного цвета, пришедшие в разных фазах, возможно, будут гасить друг друга. Насколько это соответствует действительности не совсем до конца понятно, вряд ли полностью изучена природа света и уж никто не скажет - так же освещает положительная часть волны, как и отрицательная, тем более, что это все условности математической модели, в действительности колебания электрической и магнитной составляющей, описываемые уравнениями Максвелла намного сложнее. Но никто нам не запретит поэкспериментировать с нашей моделью.
Реализация на Visual Basic'e занимает с отладкой минут 30-40 и сторицей окупается открывшейся красотой. Итак, зададим два отверстия.

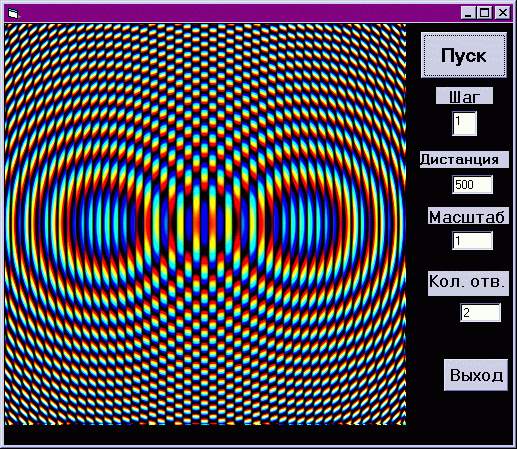
Это и есть интерференция волн от двух когерентных источников. Так и хочется сказать, что мы видим стоячие волны, но сомневаюсь, могут ли быть стоячие волны у электромагнитного излучения, хотя может нечто подобное происходит в лазерах? Кстати здесь мы прикасаемся к чуду, предсказанному теоретиками - эти два кванта света, близнецы, получившиеся при дифракции, в дальнейшем поддерживают друг с другом связь и изменения условий распространения одного из них непонятным образом становится известным второму. Возможно, здесь заложены перспективы столь любимых фантастами передачи информации быстрее света, сверхмощных квантовых компьютеров и всяких нуль-транспортировок материи. И наши опыты пусть маленький, но шажок в этом направлении, поэтому к листингу программы отнесемся трепетно.

Dim x1(), y1(), a1(), L1() Private Sub Form_Load() End Sub Private Sub Комманда1_Click() r = 100 pi = 4 * Atn(1) x0 = 200 y0 = 200 'L = 500 ampl = 250 'ss = 3 wr = 1.01 wg = 1.005 wb = 1 'num = 3 ReDim x1(num), y1(num), a1(num), L1(num) For u = 1 To num x1(u) = x0 + r * Cos(2 * pi * u / num) y1(u) = y0 + r * Sin(2 * pi * u / num) Next u For x = 1 To x0 * 2 Step ss For y = 1 To y0 * 2 Step ss qr = 0: qg = 0: qb = 0 For u = 1 To num L1(u) = ((x - x1(u)) ^ 2 + (y - y1(u)) ^ 2 + L ^ 2) ^ 0.5 / scal * 2 qr = qr + Int(ampl * Sin(L1(u) / wr)) qg = qg + Int(ampl * Sin(L1(u) / wg)) qb = qb + Int(ampl * Sin(L1(u) / wb)) Next u If KeyAscii = 32 Then End qrr = qr If qrr < 0 Then qrr = 0 qgg = qg If qgg < 0 Then qgg = 0 qbb = qb If qbb < 0 Then qbb = 0 col = RGB(qrr, qgg, qbb) If ss > 1 Then Line (x, y)-Step(ss, ss), col, BF If ss = 1 Then PSet (x, y), col Next y Next x End Sub Private Sub Комманда2_Click() End End Sub Private Sub Form_KeyPress(KeyAscii As Integer) If KeyAscii = 27 Then End End Sub

В приведенной программе переменные L (расстояние от непрозрачной стенки с отверстиями вместо кристалла до экрана), ss (шаг прорисовки) и num (количество отверстий) помечены как комментарии, так как они задаются из формы. Это позволяет, однажды запустив программу, экспериментировать с этими параметрами и каждый раз вскрикивать от восхищения. Переменная r это радиус окружности, на которой расположены отверстия, x0 и y0 - координаты центра этой окружности. Ampl - амплитуда колебания, выбирается с учетом того, что максимальное значение каждой из трех цветовых составляющих в формате RGB(red,blue,green) равно 255.
У компьютерных опытов все-таки есть преимущества перед реальным опытами. И главное из них - возможности оперировать цветами. При вычислении фазы синусоид в каждой точке экрана от каждого источника пришлось задаться длиной волны света (без учета реального масштаба), поэтому можно задать эту длину разной для разных цветов (как это и есть на самом деле). Видели же радужные полоски, если смотреть на солнце сквозь ресницы? В программе задана длина зеленой волны на пол процента больше длины волны синей, а длину волны красной на пол процента больше зеленой (переменные wr, wg и wb). Поэтому при относительно большой дистанции от источников света до экрана три луча успевают "расслоиться" и дать яркую цветную картинку.

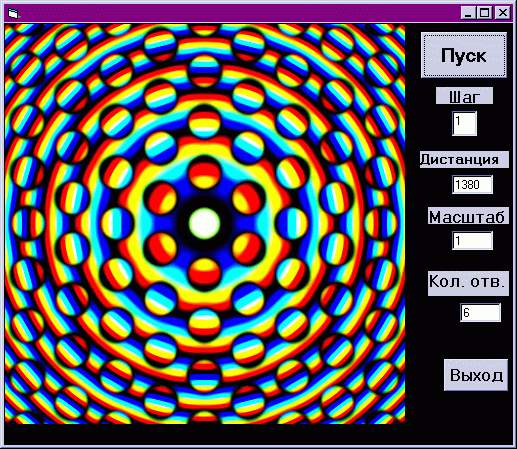
(Не объяснит ли кто-нибудь появление этих шариков, похожих на капли?) А при дистанции равной нулю наоборот, все три луча приходят вместе, что дает картинку почти черно-белую

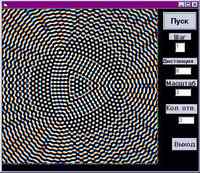
В этом случае, понятное дело, волны распространяются только в плоскости экрана, как на поверхности воды. Убедиться в справедливости модели можно создавая колебания на поверхности воды тремя источниками. (Ох уж эти три источника...)
Из-за того, что некоторые картинки давали слишком мелкую рябь, пришлось ввести возможность масштабирования (переменная scal, задается из формы программы). Сравните две картинки, созданные семью источниками, трудно выбрать, какая красивее.
  
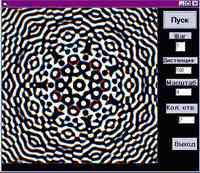
А еще сравните две картинки, отличающиеся только расстоянием от плоскости отверстий до экрана и я уверен, что вы снова затруднитесь сказать, какая из них красивее.





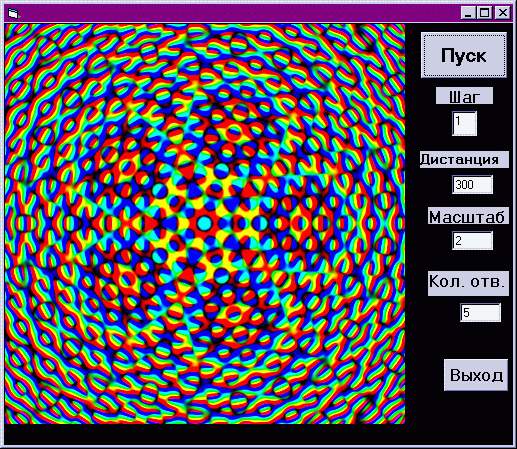
Как вы уже заметили, при задании n отверстий появляется подобие n-угольника, который лежит в основе всего узора, растягиваясь и повторяясь. При увеличении количества отверстий появляются "соцветия" с количеством лепестков, равным количеству отверстий.

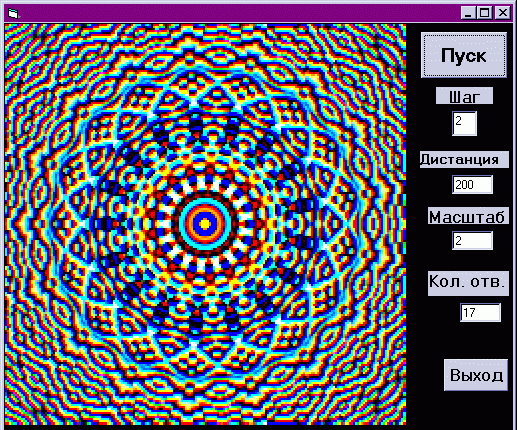
Но до определенного предела, связанного, возможно, с разрешением дисплея. При увеличении числа отверстий более двадцати лепестки сливаются и дают концентрические круги (как от одного большого отверстия), чего, впрочем, и следовало ожидать.
Для особо въедливых читателей поясню, что источник света подразумевается один, но бесконечно удаленный, так, что лучи от него параллельны. Желающие могут рассмотреть точечный источник, расположенный вблизи стенки с отверстиями. Дифракционная картина будет другой, но, уверен, не менее красивой. В идеале хотелось бы, чтобы изображение плавно менялось вслед за изменением расстояниями до экрана, до источника света и между отверстиями. Вот и все, поблагодарим кристаллографию за подсказку заняться дифракцией и еще раз удивимся, как, оперируя только синусом, можно получить такую красоту.


Часть 3, размышления в воде.

Загадывать загадки да изредка отгадывать их - единственная игра, в которую ему приходилось играть давным-давно с другими чудными зверюшками, сидевшими в своих норках. С тех пор он потерял своих друзей, стал изгнанником, остался один и заполз глубоко-глубоко, в самую тьму под горой.
Дж. Р. Толкин. Хоббит или туда и обратно

В введении к статье предлагалось во время купания в ванне проводить всякие эксперименты, как это делали великие деятели - Козьма Прутков, наблюдавший круги на воде, и Архимед, вытеснявший воду телом. Если что-то делать совсем лень, то можно просто поразмышлять над некоторыми вопросами, чтобы принятие ванны не выглядело пустым времяпрепровождением.

Что было бы, если бы показатель преломления воды увеличился в десятки или сотни раз - увидели бы мы свое тело под водой? Увидели бы что-нибудь из-под воды?

Айсберги во время плавания подтаивают снизу и иногда переворачиваются. Как это объяснить - ведь как бы айсберг не подтаивал, все равно он на 7/8 под водой, и центр тяжести намного ниже поверхности воды? Можете ли вы нарисовать конфигурацию айсберга, собирающегося перевернуться? А помните, во всех книжках по занимательной физике приводится плавающая вертикально горящая свеча - она не гаснет, пока весь парафин не израсходуется. И не переворачивается - ведь она тает сверху, а не снизу.

А вы любите ледяные ванны или душ? По мнению Н. Козлова, автора "Философских сказок", проповедующего облегченное отношение к межчеловеческим отношениям, эти процедуры связаны с психоэмоциональным стрессом, влияющим на дальнейшее поведение. Запечетлевается в подсознании и поза этой жуткой процедуры. Так вот, под ледяным душем мы стоим с гордо поднятой (возможно) головой, а в ванне лежим смиренно, еще и скрестив руки на груди, так что выбирайте. Но, хватит мерзнуть, добавим горячей воды, решая попутно изящную задачу. В ванне, наполненной до сливного отверстия, было М1 кг воды с температурой Т1. Включили кран, добавляющий М2 кг в минуту воды с температурой Т2, причем таким образом, что вода сразу перемешивается и излишки утекают в сливное отверстие. Какая температура воды будет через t минут? А если излишки не утекают - как изменится ответ? Осторожно - не залейте излишками нижний этаж.

Если аккуратно положить канцелярскую скрепку на воду, то она не утонет, ее удержит поверхностное натяжение. Если же добавить в воду мыла, то скрепка тонет, поверхностное натяжение стало меньше. Но ведь именно мыльная вода дает пену, не кажется ли вам эти факты противоречивыми? В каком месте лопаются мыльные пузыри? Откуда на пузыре радужная полоска?

Если стакан поднимать из-под воды вверх дном, то в нем будет вода. Заплывет ли туда рыбка и что с ней произойдет, если она будет плыть вверх? Стакан, естественно, не ограничен в размерах. Что будет с аквалангистом, поднимающимся в таком стакане?

Если в банке с водой проделать сбоку отверстие, то будет ли в него выливаться вода при свободном падении банки?

Если вертикальный фонтанчик, на котором держится шарик, немного наклонить, что произойдет с шариком? Вращается ли шарик на струе?

Направьте струю на стену и рассмотрите форму растекания воды по стене - парабола ли это? Как меняется ее вид при наклоне струи? Вернемся к фонтану - направим струю вертикально вверх и представим, что высота ее соизмерима с радиусом Земли (что нам стоит). Отклонится ли макушка фонтана от вертикали? Сопротивление воздуха и все ветра не рассматривать. Если да, то в каком направлении? А при падении воды на Землю - вернется ли она к источнику или упадет в другом месте? В какую сторону от источника сместится точка падения? А если мы находимся на полюсе?

Почему тоненькая струя падает в воду бесшумно, при увеличении потока до некоторого предела появляется шум, причем еще до перехода из ламинарного в турбулентный режим?

Душ и чашка помогут справиться с непростой задачей. Если дует ветер, то измениться ли количество дождевой воды, попадаемой в ведро по сравнению с безветренным дождем? Очевидно да. А если в безветренную погоду не стоять, а идти с ведром? Очевидно нет, не изменится. А если при ветре идти со скоростью ветра, естественно, по ветру? Очевидно что? Не торопитесь, это все не так просто.

Почему при размешивании чая в стакане чаинки собираются на дне в центре? А где будут чаинки если стакан будет вращаться на диске? Чай горячий после ванны - милое дело. После, а пока задача из Арифметики Магницкого (напечатанной 300 лет назад) про заварку: некто имеет чай трех сортов - цейлонский по 5 гривен за фунт, индийский по 8 гривен за фунт и китайский по 12 гривен за фунт. В каких долях нужно смешать эти три сорта, чтобы получить чай стоимостью 6 гривен за фунт? Единственно ли решение? Кстати, и Архимед, по легенде, решал задачу о доле золота в короне греческого царя, когда открыл свой великий закон.

Кто проходил "Грозу" Островского в школе помнит, как одна купчиха опасалась: вдруг пароход выйдет на глубокое место - он же утонет! Если вы считаете ее недалекой, то попробуйте ответить на вопрос: если из лодки, плавающей в бассейне, выбросить в воду (нет, не княжну) большой камень, изменится ли уровень воды в бассейне? Не торопитесь, вы наверняка ошибаетесь. А если утопить плавающую лодку - что будет с уровнем воды в бассейне?

Цистерна с водой, стоящая на тележке без трения, с одной из сторон имеет краник, направленный вниз. Сдвинется ли цистерна после того, как вся вода вытекла через краник? А в процессе вытекания? А если краник направлен горизонтально? А как посчитать угол отклонения гибкого душа, зная длину его, массу и расход воды?

На наклонной плоскости (пусть под углом ( к горизонту) стоит невесомый цилиндрический стакан (радиус окружности r) в который капают капли (массой m). После какой по счету капли стакан опрокинется? Капает, естественно, вода.

Если есть карандаш, окуните его в воду наполовину и посмотрите на его тень на дне ванны - она имеет перемычку? Почему?

Задремав в теплой ванне можно невзначай отправиться в космос на межпланетную станцию. Если верить фантастам (а кому же ещё верить?), то эти самые станции будут в виде тора для создания искусственного тяготения за счёт вращения. Такую станцию можно увидеть, например, на картинке-заставке, входящей в пакет MS PLUS98.

Итак, мы внутри. Где верх, где низ? Что покажет отвес, и как будет падать груз - по отвесу, или нет? Предположим, вы проснулись на космической станции, и не помните вчерашних событий. Как, не выглядывая в окно, определить: сила тяжести в вашей ванной комнате за счет гравитации или за счет центробежной силы от вращения станции? Первым делом напрашивается маятник. Как будет меняться плоскость его качания на вращающейся станции? Как он будет качаться в плоскости вращения тора? Как мы отличим его от маятника Фуко? Если мы подпрыгнем вертикально вверх, то на станции во время полета в прыжке сила тяжести на нас не действует, остается лишь линейная скорость касательная к тору. Пол снова "подхватит" нас, но той ли точкой, на которую мы бы опустились при гравитации? Как будет вести себя волчок? Куда полетит воздушный шарик на станции? Какие силы действуют на молекулы воздуха в комнате? Достаточно ли вращения для создания нормального атмосферного давления? Почувствует ли рыбка в аквариуме подмену гравитации? Если бежать против вращения станции со скоростью, равной линейной скорости станции, то можно обрести невесомость, а если в сторону вращения?

Однако, вернемся в ванну. Все опыты с жидкостями будут неполны без задачи на переливание, вот самая распространенная, присутствующая во всех занимательных сборниках. Восьмиведерный бочонок надо разделить пополам пользуясь трех- и пятиведерными бочонками.

И, под занавес, если это выражение подходит к купанию, классика "водяных" задач - о трубах, наполняющих бассейн. Холодный кран, открытый полностью, наполняет ванну за 10 минут. Открытые оба наполовину холодный и горячий краны наполнят ванну за 20 минут. За сколько минут наполняет ванну горячий кран? Попытайтесь объяснить полученный результат и, особенно, воспроизвести его в своей ванне. Все, можно вытираться. Парадоксы, связанные с воронкой при сливе, пением в ванне, снежинками, туманом и кессоновой болезнью рассмотрим при следующем купании.


Часть 4, волнообразная

В синем небе звезды блещут,
В синем море волны хлещут;
Туча по небу идет,
Бочка по морю плывет.
А.С. Пушкин. Сказка о царе Салтане.

Размышляя над программой дифракции лучей, проходящих через отверстия в экране, и аналогией с колебаниями воды, придем к плодотворной мысли - выйти из плоского изображения в трехмерное. В каждой точке экрана можно определить не только цвет лучей, но и суммарную амплитуду колебания (в произвольном масштабе) в направлении оси Z перпендикулярно плоскости экрана XY.

Dim x1(), y1(), a1(), L1()<br> Private Sub Form_Load()<br> End Sub<br> Private Sub Комманда1_Click() Cls DrawWidth = 2 r = 100 pi = 4 * Atn(1) x0 = 200 y0 = 200 'L = 500 ampl = 555 / num 'ss = 3 wr = 1.01 wg = 1.005 wb = 1 'num = 3 ReDim x1(num), y1(num), a1(num), L1(num) For u = 1 To num x1(u) = x0 + r * Cos(2 * pi * u / num) y1(u) = y0 + r * Sin(2 * pi * u / num) Next u xx1 = 0: yy1 = 0 For y = 1 To y0 * 2 Step ss For x = 1 To x0 * 2 Step ss qr = 0: qg = 0: qb = 0: z = 0 For u = 1 To num L1(u) = -((x - x1(u)) ^ 2 + (y - y1(u)) ^ 2 + L ^ 2) ^ 0.5 / scal * 2 qr = qr + Int(ampl * Sin(L1(u) / wr)) qg = qg + Int(ampl * Sin(L1(u) / wg)) qb = qb + Int(ampl * Sin(L1(u) / wb)) z = z + ampl * Sin(L1(u)) / 5 Next u If KeyAscii = 32 Then End qrr = Abs(qr): qgg = Abs(qg): qbb = Abs(qb) col = RGB(qrr, qgg, qbb) xx = x * Cos(pi / 12) + z * Sin(pi / 12): yy = y + z * Cos(pi / 12) If x > 1 Then Line (xx, yy)-(xx1, yy1), col xx1 = xx: yy1 = yy Next x Next y End Sub Private Sub Комманда2_Click() End End Sub Private Sub Form_KeyPress(KeyAscii As Integer) If KeyAscii = 27 Then End End Sub

Для прорисовки нашей трехмерной модели в аксонометрии приведем расчетные оси X,Y и Z (локальной системы координат) к абсолютной системе координат нашего экрана, не того виртуального, а реального монитора. Локальная ось X пустим под 150 к горизонтали, ось Z под 150 к вертикали, ось Y оставим без изменения - по вертикали, то есть отклонения по локальной оси Z проектируются на абсолютные X и Y. Все эти значения можно менять, получая новые и новые картины.


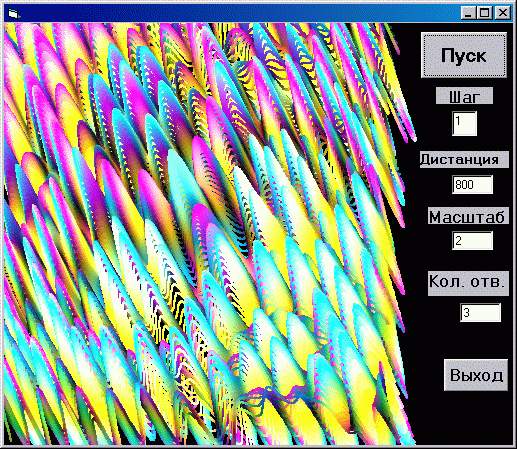
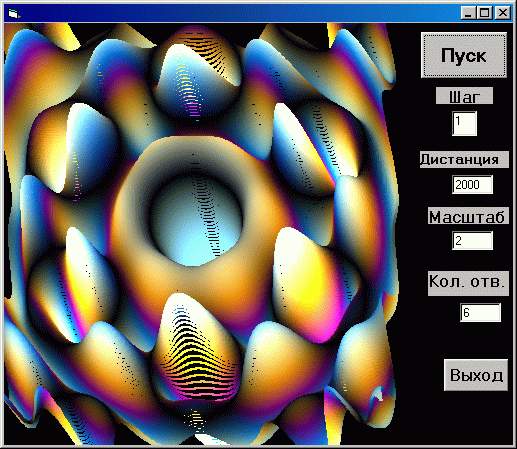
Раскраску наших волн оставили без изменения - как при дифракции. Меняя масштаб, количество отверстий и расстояние до экрана вы будете получать картины невиданной красоты - радужные торты, марсианские пейзажи и объемные орнаменты.
    Поверхности рисуются плавными линиями, а те, в свою очередь, состоят из отрезков ломанных линий, проводимых от текущей рассчитываемой точки (xx,yy) к предыдущей посчитанной точке (xx1,yy1). В конце каждого цикла текущая точка "становится" предыдущей, вспомогательные координаты xx1 и yy1 получают значения xx и yy соответственно. Этот прием используется при рисовании трехмерных поверхностей и других геометрических моделей, мы о них еще поговорим.

Часть 4, радужная

На синее бросаться не с руки:
Волну сожмёшь, и цвет уйдёт из вида.
Об этом помнят умницы быки,
Когда идёт красавица коррида.
http://www.dol.ru/users/levinb/glup_fr.htm

Вряд ли вы назовете природное явление, которое может соперничать с радугою по красоте, по эмоциональному воздействию, причем всегда положительному, даже по участию в детских стишках, взрослых песнях, народных приметах и поговорках. Сейчас мы осуществим радужные мечты любителей занимательного программирования, ибо каждый охотник желает знать, как увидеть радугу на экране компьютера.
    Это совсем не сложно. Причем мы не будем углубляться в тонкости дисперсии световых лучей в водяных каплях, а просто осветим экран, как и в опытах с дифракцией, но из единственной центральной точки. А каждый цвет будет прилетать в точки экрана в своей фазе, и, смешиваясь с двумя другими составляющими должен порождать радужные концентрические круги.

Dim x1(), y1(), a1(), L1() Private Sub Form_Load() End Sub Private Sub Комманда1_Click() Cls pi = 4 * Atn(1) wr = 15 wg = 12 wb = 14 DrawWidth = 4 For Ll = 1 To 500 Step 3 For r = 1 To 200 Step 5 fi = Atn(r / Ll) red = 255 * ((Sin(fi * wr - pi / 8)) ^ 2) green = 255 * ((Sin(fi * wg - pi / 8)) ^ 2) blue = 255 * ((Sin(fi * wb - pi / 8)) ^ 2) Circle (200, 200), r, RGB(red, green, blue) Next r Next Ll End Sub Private Sub Комманда2_Click() End End Sub Private Sub Form_KeyPress(KeyAscii As Integer) If KeyAscii = 27 Then End End Sub

Что мы и видим на скриншотах.
      
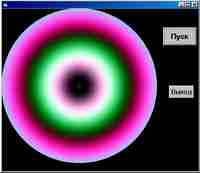
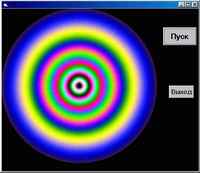
Учитывая, что радужная картина зависит от расстояния между отверстием и экраном и не хочется пропустить какой-либо красивый вариант, будем менять это расстояние в цикле (переменная L1) от 1 до 500. Это позволит наблюдать на экране концентрические радужные круги, растущие от центра с постоянным изменением раскраски. Учтите, что если вы захотите сделать скриншот меняющихся радужных колец, то у вас всегда будет запоминаться последняя картинка, не зависимо от того, в какой момент вы нажимали Alt+Print Screen. Дело в том, что пока работает цикл и рисуется картинка, Visual Basic "берет на себя" все события Windows, все внешние команды откладываются до завершения цикла.
    Чем-то эти картинки похожи на радужную оболочку глаза, которая, как известно, содержит полную информацию об организме. А может, это монитор смотрит на нас с вами, причешитесь и улыбнитесь на всякий случай.


Часть 5, Ссылки

Странички, посвященная зрительным иллюзиям - это
http://www.psy.msu.ru/illusion/

и http://imp-world-r.narod.ru/ ,

также об иллюзиях смотрите Компьютерные вести http://www.kv.by/index2000464401.htm

Интересная статья о Пенроузе и его идеях в кристаллографии расположена на http://www.computerra.ru/cgi/yandmarkup?HndlQuery=855297216&PageNum=0&g=0&d=0  

На Речке www.rechka.ru  есть аплет, моделирующий распространение волн на поверхности жидкости.

О чаинках в стакане и прочих водных парадоксах смотрите на http://www.inp.nsk.su/~baldin/Encyclopedia-4/Physics/node6.html

О переворачивающихся айсбергах и почти все о воде смотрите на http://www.n-t.org/ri/ar/zv01.htm

О поверхностном натяжении популярно здесь: http://www.n-t.org/tp/ns/mr.htm.


Занимательные сведения о торе на Арбузе здесь, а о пузырях - здесь.