Гиперболические поверхности

Знакомые дали почитать "Книжку с картинками по топологии" (Дж. Франсис, М., Мир, 1991), в самом начале которой рассматриваются седлообразные поверхности. Захотелось попробовать тоже, и вот что получилось:.

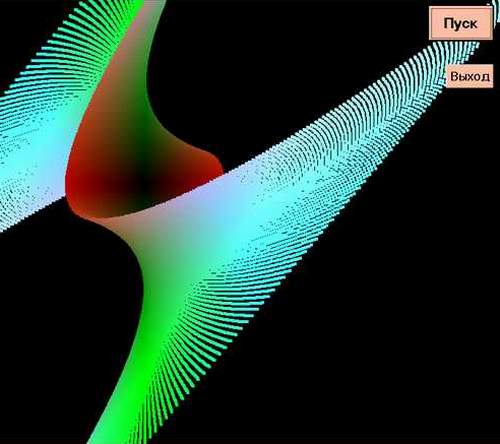
Уравнение этой поверхности Z=X*Y²

Следующая картинка:

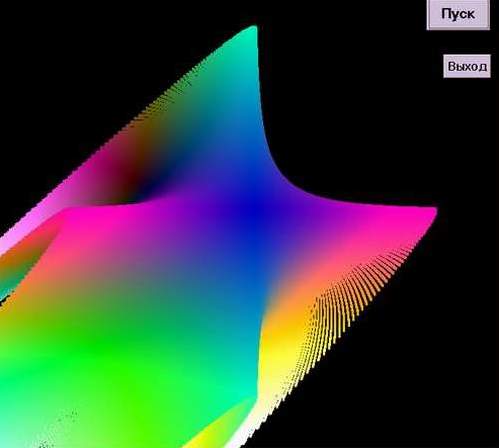
получается из уравнения Z=X²*Y²

А если внести небольшие изменения в формулу, пытаясь раздвинуть вершины 
z = (x + 50) * (x - 50) * (y + 30) * (y - 30),
то увидим, как края начинают загибаться вверх:

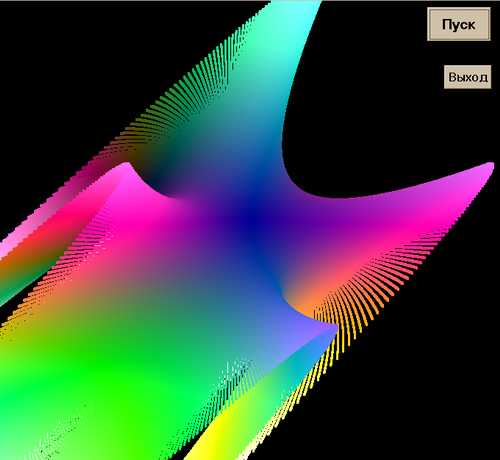
Дальнейшую деформацию седла можно получить, воспользовавшись уравнением
z = (x + y) * x * y

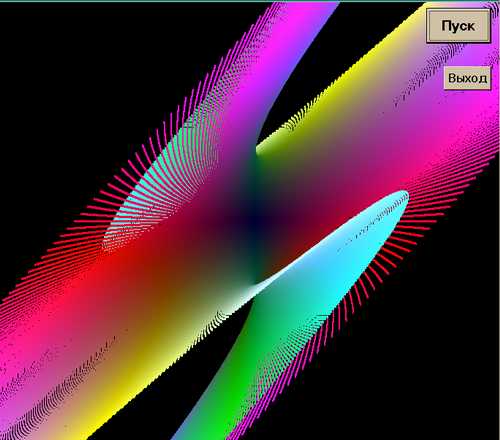
Ну а теперь просто этюд (с колючкой):

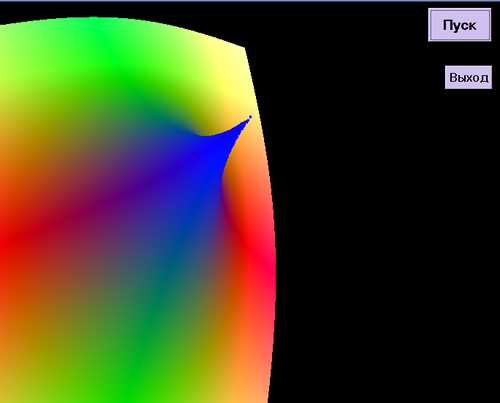
с формулой (в кодах бейсика)  z = ((x * x + y * y) * 80000) ^ 0.25

А это две ветки гиперболоида, вырождающиеся в точку в начале координат.

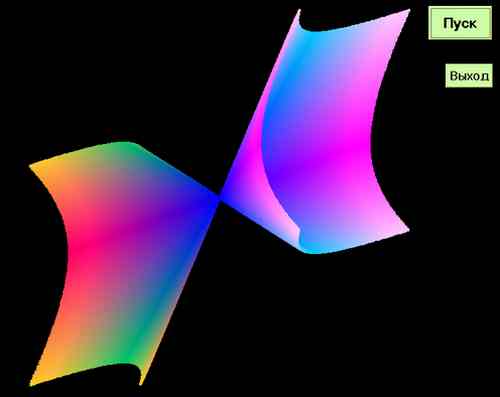
Уравнение Z=X²+Y² То есть видно, что координата по Z - это корень квадратный из радиуса окружности в плоскости XY.

А теперь граница между ветвями не вырождается в точку..

Ну и представлю теперь код, чтобы могли построить:
Private Sub Комманда1_Click() Cls DrawWidth = 1 pi = 4 * Atn(1) x0 = 250 y0 = 180 ss = 1.3 ReDim x1(num), y1(num), a1(num), L1(num) xx1 = 0: yy1 = 0: k = 1 For y = -y0 To y0 * 1 Step ss For x = -x0 To x0 * 1 Step ss If KeyAscii = 32 Then End k = -k t = (1000 - (x * x - y * y) * 0.24) If t > 0 Then z = k * t ^ 0.5 qrr = Abs(1 * x): qgg = Abs(2 * y): qbb = Abs(250 - z) col = RGB(qrr, qgg, qbb) xx = x * Cos(pi / 6) - z * Sin(pi / 6) yy = y + z * Cos(pi / 6) If ss > 1 Then Line (xx + 300, yy + 270)-Step(ss, ss), col, BF If ss = 1 Then PSet (xx + 350, yy + 300), col xx1 = xx: yy1 = yy Else z = 0 End If Next x Next y End Sub
Обратите внмание, кстати, как получается такая раскраска - каждая из трех составляющих цвета зависит от одной из трех координат. И как получается аксонометрия - ось Z пускаем под углом...
Если поменть знаки у x*x и y*y, то вся картинка "ложится на бок":

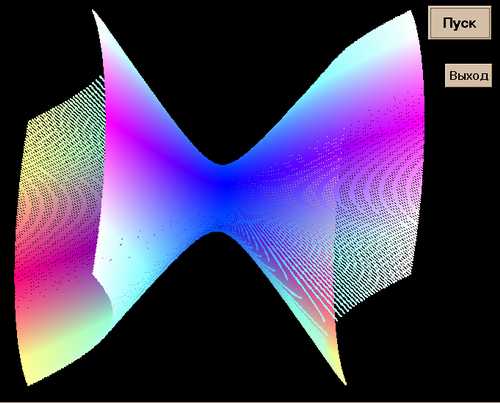
И, наконец, самые дотошные могут рассмотреть отверстие в перемычке...

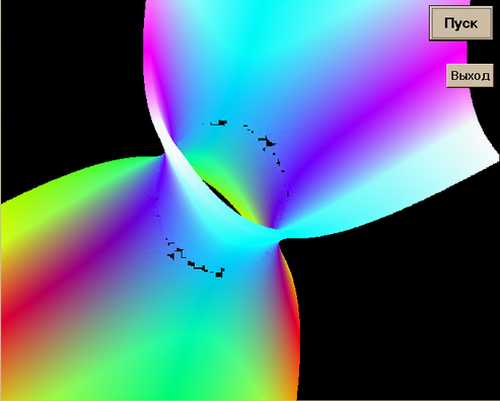
Вот и все... попробуйте повторить и получить  поверхности еще красивее. С ними прошу в Форум...