Головоломки из журнала "В мире науки"

ВЗАИМОСВЯЗАННЫЕ ПОТЕРИ

БЕЛКОВЫЙ ПЕРЕЗВОН

БЛЕФ-ЛОБ

ВЗЛОМ СЕЙФА

ВСЕ ИЛИ НИЧЕГО

ДРЕВО ЖИЗНИ

КАК ПРЕДОТВРАТИТЬ УТЕЧКУ ИНФОРМАЦИИ

МИНИ-ШАШКИ

ПРОВЕРКА МИКРОСХЕМ

РАЗВЕДЧИКИ И ПОГРАНИЧНИКИ

ПЯТЬ НАДЕЖНЫХ СИГНАЛЬНЫХ РАКЕТ

СКОРОСТНАЯ СЕТКА

СОВЕРШЕННЫЙ БИЛЬЯРД

Сайт журнала.
Спасибо Константину Кнопу за наводку и Ирине Истоминой за разрешение.

сентябрь 2003 № 9 "В МИРЕ НАУКИ"

Дэннис Шаша

Предположим, что вы решили заняться игрой в сквош. Клуб предлагает две схемы оплаты: $400 за годовой абонемент или $20 за одно посещение. Вы хотите играть несколько раз в неделю, но часто получаете травмы. Ясновидящий смог бы предсказать возможность неудачного случая и, таким образом, определить, будет ли выгоднее приобрести годовой абонемент или платить каждый раз. Не обладая сверхъестественными способностями, вы решаете разработать стратегию минимизации своего коэффициента потерь - отношения объема затраченных средств к той сумме, которую потратил бы ясновидящий.

Если бы с самого начала вы решили приобрести годовое членство в клубе и получили бы травму в первый же день, значение коэффициента потерь равнялось бы 20 – потраченные $400, поде ленные на $20, которые потратил бы провидец. Если на протяжении всего года вы будете использовать разовую оплату, сыграете 100 раз и затем получите повреждение, то коэффициент станет равным 5 – затраченные $2000 по отношению к $400, которые бы внес ясновидящий. Существует ли способ удержать значение коэффициента ни же 2 вне зависимости от получения травмы? Ответ на разминочную загадку приведен в нижней части страницы.

В математике такого рода задачи относятся к области сравнительного анализа. Рассмотрим другой пример:
у вас есть 90 билетов, которые можно обменять на деньги. В киоске, где про изводится обмен, есть стопка купюр достоинством $1 и $5. За каждый билет служащий предлагает верхнюю банкноту из стопки (либо $1, либо $5). Можно отказаться от предложения и продать билет за $1, надеясь, что позже за него дадут пятидолларовую банкноту. В этом случае билет остается у вас, а служащий откладывает в сторону однодолларовую купюру и больше к ней не обращается. В то же время киоскер в любой момент может прекратить торговлю, после чего билеты будут обесценены.

Оракул знал бы заранее, что предложит служащий и когда закончатся торги, но у вас нет такой возможно сти. Способны ли вы найти такую стратегию, которая гарантировала бы то, чтобы размер коэффициента по терь (в данном случае – доход ясно видящего по отношению к вашему) не превышал 1,8? И какова была бы ваша стратегия, если бы два доступных предложения соответствовали $1 и $1 млн.? Как это отразилось бы на значе нии коэффициента?

ОБ АВТОРЕ:
Дэннис Шаша (Dennis E. Shasha) – профессор информатики в Институте Коуранта Нью-Йоркского университета.

Ответ на «разминочную загадку»:(выделите мышкой) заплатите за 19 посещений, а затем приобре тите годовой абонемент. Если вы получите травму в первых 19 играх, ваш коэффи циент потерь будет равен 1. В случае получения телесных повреждений в после дующих играх коэффициент составит 1,95.

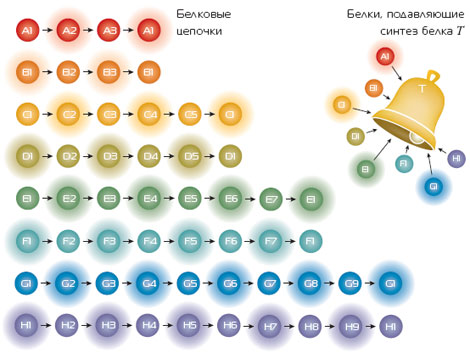
май 2003 № 5 "В МИРЕ НАУКИ"

Дэннис Шаша

В 1950-х гг. Жак Моно (Jacques Monod) и Франсуа Жакоб (Francois Jacob) из Пастеровского института в Париже обнаружили, что у кишечной палочки Escherichia coli есть белки-регуляторы, подавляющие синтез других белков. Предположим, что белок Х подавляет образование белка Y, и представим это схематически в виде Х>Y. Когда концентрация белка Х повышается (т.е. он начинает синтезироваться), концентрация белка Y через какое-то время (скажем, через секунду) начинает понижаться. Если же концентрация белка Х начинает понижаться, то через секунду концентрация Y повышается - конечно, если его синтезу ничто другое не мешает.

Предположим, что у нас три белка – А, В, С, исходя из условия, что А>В>С>А. Если А появляется, то В через секунду исчезает, затем через тот же интервал времени появляется С, а затем исчезает А. Затем все повторяется. Возникает что-то вроде биологических часов – А, В и С периодически то появляются, то исчезают. Такой механизм действительно был создан несколько лет назад Майклом Еловицем (Michael Elovitz), который в то время был аспирантом Принстонского университета.

Предположим, что вам нужно создать «белковый колокольчик», который звонил бы каждые 70 секунд. У вас есть во семь белковых цепочек, обозначенных буквами от А до Н, каждая из которых со держит три, пять, семь или девять белков. Ни один белок в любой цепочке не влияет на образование белков из других цепочек, но один из белков в каждой цепочке подавляет синтез особого белка Т, который сообщает о своем появлении «звоном». Если концентрация любого из этих восьми белков (от А1 до Н1), подавляющих образование Т-белка, увеличивается, то секундой позже Т-белок исчезает и не появляется вновь до тех пор, пока не исчезнут все восемь белков.

Чтобы «включить» любую из цепочек, вам нужно запустить синтез одного из ее белков. Например, для включения С цепочки можно поддерживать в течение 5 секунд синтез белка С4. Через од ну секунду после начала синтеза С4 концентрация С5 начнет уменьшаться, затем по порядку с интервалом в секунду появится белок С1, исчезнет С2, появится С3. Но появление С3 не вызывает исчезновение С4 к концу 5-й секунды, поскольку мы все еще поддерживаем его синтез. Таким образом, спустя еще одну секунду после того, как мы прекратили поддерживать синтез С4 (или спустя шесть секунд после того, как мы начали его поддерживать), белок С4 все еще присутствует. Затем цикл возобновляется: на 7-й секунде появляется С5, на 8-й исчезает С1. Концентрация С1 начинает снова увеличиваться на 13-й секунде, уменьшаться на 18-й и т.д.

Чтобы заставить белок Т «звонить» каждые 70 секунд, вам понадобятся только четыре из восьми приведенных выше цепочек. Необходимо определить, какие именно цепочки нужно оставить и как запускать каждую из них, т.е. синтез какого белка нужно поддерживать и как долго. Вы можете поддерживать синтез какого-то белка в течение 15 секунд, а затем «часы» должны начать работать самостоятельно.

июль 2004 № 7 "В МИРЕ НАУКИ"

Дэннис Шаша

В детстве я любил играть в рулетку, покер и "очко" - словом, в азартные игры, где принимали ставки от трех центов. Помню, любимое наше развлечение называлось "Блеф-лоб". Каждый брал из перетасованной колоды по одной карте и прижимал ее ко лбу лицевой стороной наружу. В результате игрок видел карты всех соперников, но не видел свою. Банк забирал тот, кто вытащил самую большую карту. Туз был старшим, а масть не имела значения, так что иногда куш приходилось делить.

Я предлагаю вам научиться делать логические выводы о картах игроков, основываясь на их высказываниях. Предположим, что играют трое. Первой всегда говорит Катя, за ней Петя, потом Вася, затем снова Катя и т. д. Каждый игрок должен произнести одну из фраз, перечисленных в левом нижнем углу страницы. Допустим, что все трое в совершенстве владеют логикой и всегда говорят сильнейшую фразу, т.е. выбирают из списка самое верхнее истинное предложение.

Для разминки представьте, что Катя заявила: "Я не знаю", а Петя и Вася по очереди произнесли: "Я проиграл". Услышав сказанное, можно догадаться, что у Кати на лбу был туз, а у ребят - карты помладше. Иллюстрация поможет вам разобраться, почему это именно так.

А теперь к делу. Что вы можете сказать о картах игроков по приведенным стенограммам пяти игр?

Игра 1: Катя сказала: "Я не знаю". Петя произнес: "Я не выиграл", а Вася объявил: "Я выиграл".

Игра 2: Катя призналась: "Я не знаю". Петя молвил: "Я не выиграл". Вася изрек: "Делим куш".

Игра 3: Катя произнесла: "Я не знаю", а Петя и Вася сказали: "Я не выиграл".

Игра 4: Сначала все трое заявили: "Я не знаю", а затем Катя молвила: "Я проиграла". Как вы считаете, что потом сказали Петя и Вася?

Игра 5: Первые два раза все трое говорили: "Я не знаю". Затем Катя и Петя сказали: "Я не знаю", а Вася радостно вскричал: "Я выиграл!" Какая у него была карта и что он увидел на лбах своих товарищей?

Ответ на головоломку этого номера ищите на http://www.sciam.com/

июль 2003 № 7 "В МИРЕ НАУКИ"

Дэннис Шаша

Представьте, что вы - вор (но, конечно, добрый и справедливый, как Робин Гуд). Чтобы забраться в сейф, нужно открыть механический кодовый замок c 10 поворотными ручками, которые могут находиться в трех положениях - нижнем, среднем и верхнем. Существует ровным счетом 310 (59049) возможных комбинаций, но вам повезло: 38 (6561) из них откроют сейф. Все очень просто: если позиции двух нужных ручек правильные, то вам осталось лишь потянуть на себя дверь сейфа. Положение остальных восьми ручек не имеет значения. Вся беда в том, что вы не знаете, какие две ручки являются ключевыми (они могут располагаться и не по соседству).

Поскольку комбинаций, открывающих сейф, достаточно много, можно начать с произвольного перебора: вероятнее всего одна из девяти попыток окажется удачной. Но фортуна часто отворачивается от вас, поэтому необходима полная гарантия, что взлом пройдет быстро. Можно ли открыть сейф, перебрав менее 20 комбинаций? Если – да, то какие комбинации следует попробовать?

Вот вам задачка для разминки. Пред положим, кодовый замок состоит все го из четырех поворотных ручек с тремя положениями, и для открытия сейфа необходимо поставить две из них в правильную позицию. Сколько комбинаций нужно перебрать, чтобы наверняка открыть сейф? Если бы вы знали, какую пару ручек нужно повернуть, вам все равно пришлось бы испытать девять различных комбинаций. (Давайте буквой А обозначим верхнюю позицию ручки, буквой В – сред нюю, а буквой С – нижнюю. Теперь эти комбинации можно перечислить как АА, АВ, АС, ВА, ВВ, ВС, СА, СВ и СС.) Но даже не зная, какие две ручки ключе вые, можно открыть сейф с четырьмя ручками менее чем за 12 попыток (см. рис. внизу). Как видите, в довольно ко ротком перечне содержатся все девять комбинаций для любой пары ручек независимо от их местоположения. Сможете ли вы теперь составить подобный список комбинаций для замка с десятью ручками?

Набор комбинаций для взлома сейфа с четырьмя ручками

Первая
ручка Вторая
ручка Третья
ручка Четвертая
ручка

1. A C C C

2. B B B C

3. C B A A

4. A A B A

5. A B C A

6. B A A B

7. C A A C

8. B C C A

9. C C B B

10. C A C B

11. A C A A

май 2004 № 5 "В МИРЕ НАУКИ"

Дэннис Шаша

Любое сообщение можно представить в виде последовательности чисел. Например, слово "Встреча" в предложении "Встреча на площади Революции" большинством компьютеров, использующих кодировку ANSI 1251, трактуется как 194 241 242 240 229 247 224.

Допустим, вам нужно послать секретное сообщение с пятью курьерами. Опасаясь, что одного или двух из них перехватят, вы решили распределить информацию так, чтобы для ее полного восстановления требовалось поймать как минимум троих посыльных.

Поскольку сообщение закодировано числом, проще всего было бы раздать каждому курьеру только определенную его часть. Однако это не самый безопасный подход. Лучше организовать информационный «обрыв»: сделать так, чтобы любые два посыльных не могли сообщить никаких полезных сведений, а любые три были в состоянии передать все сообщение полностью.

Для разминки представьте, что я выбрал на плоскости точку, например с координатами 13 и 6, и попросил трех товарищей найти ее. Желательно, чтобы никто не мог справиться с заданием в одиночку, но без труда получил правильный ответ, обратившись за помощью к любому из двух друзей.

Маше я сообщил, что точка лежит на линии x=13, Васе – что она расположена на прямой y=6, а Кате – что искомые координаты связаны соотношением y=x–7 (см. рис. внизу). Как мои товарищи могут использовать полученную информацию?

Согласныли вы, что для успешного поиска необходимо и достаточно получить сведения, известные любой паре? Подобные рассуждения помогут вам решить задачу о пяти курьерах.

ОТВЕТ: (выделите мышкой) Пусть число, в котором зашифровано ваше сообщение, станет координатой x точки P в трехмерном пространстве. Две другие координаты выберите произвольно. Затем задайте 5 плоскостей, пересекающихся в этой точке, и присвойте каждую из них одному из курьеров, определив тремя точками, отличными от P
Пересечение двух непараллельных плоскостей определяет прямую, а любая непараллельная ей плоскость пересекает ее в искомой точке. Знание двух плоскостей для врага бесполезно, т.к. они не помогут найти заветную точку. Но любые три курьера легко отыщут ее, узнают координату x и расшифруют сообщение.

РАЗМИНОЧНАЯ ЗАДАЧА: Как вдвоем отыскать точку с координатами (13, 6), если ее нельзя найти в одиночку?

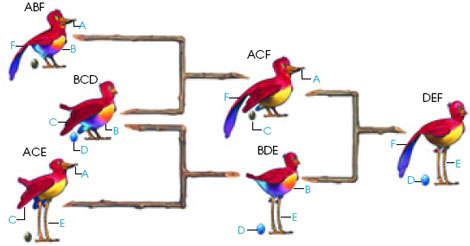
ОТВЕТ: (выделите мышкой) Информация об одной линии бесполезна: искомая точка может лежать на ней где угодно. Но двое друзей могут мгновенно справиться с заданием, найдя пересечение известных им прямых.

август 2003 № 8 "В МИРЕ НАУКИ"

Дэннис Шаша

Развитие жизни на Земле нередко изображают в виде древа, предполагая при этом, что каждый из ныне существующих видов ведет свое происхождение от одного предкового вида. Новый вид возникает после того, как некая популяция исходного вида адаптируется к новым условиям существования и начинает настолько сильно отличаться по своим генетическим характеристикам от основной группы, что их представители теряют способность к скрещиванию друг с другом. Так выглядит общепринятая теория видообразования, однако биологии абсолюты не свойственны. Результаты многочисленных исследований заставляют предполагать, что, хотя представители разных видов обычно не скрещиваются, скрещивание между ними вполне возможно. Более того, время от времени такая гибридизация приводит к появлению новых видов.

Представьте теперь, что вам нужно проследить эволюционные взаимосвязи в некой группе видов. Известно, что одни из них – исходные (предковые) виды, а другие – производные. Прямы ми эволюционными предками вида Х будут те виды группы, которые, скрещиваясь, обеспечивают вид Х всеми присущими ему признаками (никакой другой вид в этом процессе не участвует). Заметим, что новый вид – Y может образоваться в результате объединения генетического материала трех видов, причем в этом случае сначала образуется некий невидимый промежуточный вид. Следует, однако, считать, что вид Y имеет трех прямых предков, т.к., прослеживая его происхождение, мы учитываем только те виды, которые можно увидеть. И еще од но ограничение: ни один вид не может возникнуть прежде, чем на свет появятся его предки.

Разминка. Предположим, имеются три исходных вида с признаками ABF, BCD и ACE, соответственно, и три производных с признаками ACF, DEF и BDE. Постройте эволюционную схему, которая предполагает наличие у каждого производного вида максимум двух прямых предков (которые могут быть и производными видами). Одно из решений задачи представлено внизу.

Задача. Предположим, четыре исходных вида имеют признаки AB, DH, EF и CG, а производные – признаки BEF, DEF, ADE, ACD, ACF, ADG, BEG и FGH. Постройте эволюционную схему, где каждый из производных видов, за ис ключением одного, имел бы только двух прямых предков. (Как и в разми ночном примере, один или оба из них могут быть производными видами). Можете ли вы найти четыре альтерна тивных предковых вида с двумя при знаками, чтобы при этом: а) каждый из производных видов имел только двух прямых предков; b) эволюцион ный путь от исходного вида к произ водному включал не более одного промежуточного вида?

Одно из решений разминочной задачи: ACF возник непосредственно от ABF
и BCD, BDE – от BCD и ACE, а DEF – от ACF и BDE.

ОБ АВТОРЕ:
Дэннис Шаша (Dennis E. Shasha) – профессор информатики в Институте Коуранта Нью-Йоркского университета.

ОТВЕТ НА ЗАГАДКУ:(выделите мышкой)
В первой задаче, BEF происходит непосредственно от AB и EF;
DEF – от DH и EF;
ADE – от AB и DEF; ACD – от ADE и CG;
ACF – от ACD и EF; ADG – от ACD и CG;
BEG – от BEF и CG. Для появления FGH требуется 3 промежуточных вида.
Во второй задаче четырьмя альтернативными предковыми видами будут BE, DF, AC и GH.

апрель 2003 № 4 "В МИРЕ НАУКИ"

Дэннис Шаша

Директор правительственной организации делится конфиденциальной информацией с девятью сотрудниками, а на следующий день она появляется в газетах. Для того чтобы выявить виновного в утечке сведений, сообщают каждому из подозреваемых некоторую часть важной информации, а затем контролируют ее появление в периодике. Однако публикация появится только в том случае, если она подтверждена не менее чем тремя источниками. Руководитель же уверен, что виноваты в утечке не более трех сотрудников.

Перед директором дилемма: если он сообщит информацию всем, она, безусловно, будет опубликована, однако он ничего не узнает. Он может сообщать фрагменты информации, разделив группу на тройки, и смотреть, в каком случае появится публикация. Однако девять сотрудников могут образовать 84 тройки, а это слишком много. Вырабатывается стратегия: группа будет разделена на четверки, каждой из которых будет сообщаться по одному фрагменту в день. Когда утечка обнаружится, он сможет сузить количество подозреваемых троек. Одной из его идей было провоцировать не более двух утечек - одну из четверки и одну из тройки. Другая мысль - подобрать такую последовательность четверок, чтобы гарантировать ровно одну утечку и точно определить троих злоумышленников, испробовав при этом не более 25 порций ценной информации. Можете ли вы ему помочь?...

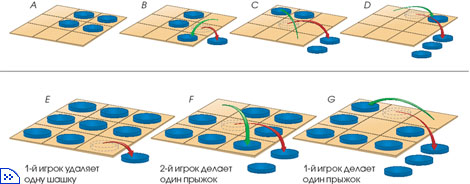
август 2004 № 8 "В МИРЕ НАУКИ"

Дэннис Шаша

Представьте себе доску 3і3 клетки, на которой расставлены шашки. Правила игры просты: одна шашка может перепрыгивать через другую в горизонтальном, вертикальном или диагональном направлении, если за ней есть свободная клетка. Шашка, через которую совершен прыжок, удаляется с доски как в обычных шашках.

Если играет один человек, то его задача - оставить на доске всего одну шашку. Рассмотрим положение, показанное на рис. А. Как удалить с доски все шашки, кроме одной? Решение показано на рис. B, C и D.

Для начала попытайтесь ответить на два вопроса: каково должно быть минимальное количество пустых клеток в начале игры, чтобы гарантировать возможность победы, и как они должны быть расположены? Попробуйте решить эту же задачу для доски 4х4 клетки.

Играть можно и вдвоем. Сначала на каждую клетку доски ставится одна шашка. Затем первый игрок снимает шашку с любой клетки. Второй игрок делает прыжок какой-нибудь шашкой и при желании продолжает прыгать ею, если у него появляется такая возможность. Затем точно так же ходит его партнер и т.д. Игра продолжается до тех пор, пока один из игроков не победит, сделав прыжок, после которого на доске останется всего одна шашка. Если после прыжков соперника игрок не может прыгнуть ни одной шашкой, то он должен передвинуть одну из них на центральную клетку. Если и этого сделать нельзя, то он обязан передвинуть любую нецентральную шашку на свободную соседнюю клетку.

Первые три возможных хода такой игры показаны на рис. E, F и G. Как вы думаете, кто выиграет, если оба игрока будут использовать оптимальные стратегии? (Ответ смотрите в следующем номере.)

ВЕРСИЯ ДЛЯ ОДНОГО ИГРОКА

ВЕРСИЯ ДЛЯ ДВУХ ИГРОКОВ

Подробное решение ищите на сайте http://www.sciam.com/

апрель 2004 № 4 "В МИРЕ НАУКИ"

Дэннис Шаша

Вы только что получили большую партию цифровых микросхем от не очень надежного поставщика. Вам точно известно, к каким участкам чипа ведут его внешние выводы. Более того, изготовитель сообщил, что представляет собой каждый элемент схемы, но верить ему нельзя. Использовав наименьшее количество тестов, вы должны определить, действительно ли поставщик установил заявленные элементы. Вся схема состоит из логических вентилей "ИЛИ" и "И", которые характеризуются таблицами истинности (см. рис. 1 и рис. 2), связывающими состояние выхода с состояниями входов. Вентиль "И" выдает единицу только тогда, когда единица присутствует на обоих входах, а вентиль "ИЛИ" - тогда, когда единица подана хотя бы на один вход.

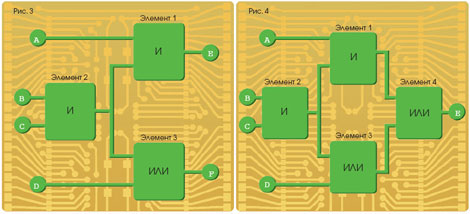
В качестве разминки рассмотрим схему с тремя элементами (рис. 3). В принципе, любой из них может оказаться как вентилем "ИЛИ", так и вентилем "И". Для проверки нужно подать комбинацию единиц и нулей на входы A, B, C, D и посмотреть, что появится на выходах E и F. В данном случае достаточно одного теста. Вопрос в том, в какие состояния следует установить входы схемы и какими должны быть ожидаемые результаты на выходах?

Ответ таков: на входы A, B, C и D нужно подать соответственно 1, 0, 1 и 1. Если все элементы указаны верно, то на выходе E появится ноль, а на выходе F - единица (можете проверить с помощью таблиц истинности). Если хотя бы один из вентилей указан неправильно, комбинация результатов на выходах будет иной.

Теперь перейдем к схеме с 4 элементами (рис. 4). Сколько нужно тестов, чтобы как можно скорее проверить ее, и что следует подавать на входы в каждом из них? Как изменится решение, если эту же схему составить из четырех вентилей "И"? Наконец, рассмотрите все возможные сочетания вентилей "И" и "ИЛИ" для предыдущей схемы (рис. 3). Какие комбинации элементов можно проверить с помощью всего одного теста?

ОТВЕТ НА ГОЛОВОЛОМКУ: (выделить мышкой)
Для проверки схемы с четырьмя элементами необходимы два теста. В первом на входы A, B, C и D нужно податьсоответственно 0, 0, 0 и 1 (сочетание0001). При этом на выходе E должнабыть единица. Во втором тесте на входы нужно подать сочетание 1010. При этом на выходе E должен быть ноль. В случае схемы с четырьмя вентилями «И» нужны три теста, в которых на входы нужно подать 0111, 1011 и 1110.
Только две трехэлементные схемы нельзя проверить с помощью одного теста: ту, в которой второй элемент – вентиль «И», а остальные – «ИЛИ», и ту, в которой второй элемент – вентиль «ИЛИ», а остальные – «И».

февраль 2003 № 2 "В МИРЕ НАУКИ"

Дэнис Шаша

Теория чисел, некогда воспринимавшаяся как эзотерическая наука о загадочных свойствах простых чисел, самым неожиданным образом вторглась в современную криптографию. Большинство электронных платежей теперь осуществляется при помощи цифровой подписи, известной как алгоритм Райвеста-Шамира-Адлемана (Rivest-Shamir-Adleman) (RSA). В его основе лежит принцип разложения числа, представляющего собой результат перемножения двух простых чисел на множители.

Перемножение двух больших простых чисел есть не что иное, как односторонняя функция. Этот процесс занимает всего несколько микросекунд, а время, затраченное на выполнение данной операции, прямо пропорционально длине этого числа, отображенного в двоичной системе. Напротив, поиск двух простых множителей числа, скажем объемом в 512 бит, может занять несколько часов. Даже после того, как искомые величины будут найдены, перебор оставшихся вариантов продолжится. Для чисел в 2 048 бит подобный процесс считается нецелесообразным, поскольку он занимает практически неограниченно долгое время. Для защиты особо важной военной и промышленной информации используются более сложные способы криптографической защиты, при которых даже сверхбыстрый поиск оказывается неэффективным.

Это подводит нас к головоломке, придуманной Джоном Маккарти (John McCarthy), - автором языка программирования Lisp и теории искусственного интеллекта. В 50-х годах Майкл Рабин (Michael Rabin), известный изобретатель прикладных и развлекательных компьютерных программ, разгадал головоломку. Сумеете ли вы?

Задача формулируется следующим образом: группа разведчиков проникает на вражескую территорию. После выполнения задания бойцы возвращаются, но при переходе границы или их застрелят свои, приняв за шпионов, или пограничники пропустят вражеских агентов на свою территорию. Чтобы избежать недоразумений, каждый разведчик должен будет назвать свой пароль, который пограничник должен будет опознать. И разведчики, и пограничники вполне надежны, но вдруг они проболтаются за кружечкой пива в баре? Итак: какого рода информацию можно доверить пограничникам, и какие пароли должны называть разведчики, чтобы только они смогли пересечь границу, даже если пограничники выдадут известные им сведения? Подсказка - рассуждение о простых числах.

Web-решение (необходимо выделить мышкой): разведчик придумывает два произвольных больших простых числа и дает пограничникам число, являющееся результатом перемножения этих чисел. По возвращении разведчик называет пограничнику эти два простых числа, тот, в свою очередь, их перемножает и смотрит, совпадает ли полученное число с ранее полученным.
Необходимо учитывать, что даже в случае, когда пограничник раскроет ранее данное число, будет практически бесполезно для противника пытаться найти множители, так как вычислительный процесс очень сложный.
Подробное объяснение можно найти на сайте http://www.sciam.com/

июнь 2003 № 6 "В МИРЕ НАУКИ"

Дэннис Шаша

Представьте, что у вас есть два комплекта сигнальных ракет по шесть штук в каждом, причем один из них содержит три бракованные ракеты, которые с виду ничем не отличаются от остальных. Единственный способ проверить ракету - поджечь ее. Однако после этого она станет совершенно бесполезной.

Теперь представьте, что вы отправляетесь на Северный полюс. Придумайте такой способ проверки, при котором вероятность выбора пяти качественных ракет составит не менее 3/4. Иными словами, сможете ли вы предложить такой метод отбора, при котором не менее 75 из 100 полярников возьмут в экспедицию по пять рабочих ракет? Как изменится вероятность, если в злосчастном комплекте окажутся не три, а четыре бракованные ракеты?

Разминка №1
Как, израсходовав не более четырех ракет, выбрать две надежные, если в испорченном комплекте по прежнему три бракованные ракеты?

Решение

Начните испытывать ракеты из любого комплекта. Если из четырех испытанных ракет окажется хоть одна бракованная, значит, вы выбрали испорченную коробку; в этом случае возьмите две любые ракеты из другого (хорошего) набора. И наоборот, если все четыре ракеты оказались качественными, значит, перед вами комплект без брака – смело берите оставшиеся две.

Разминка №2

Как при тех же условиях выбрать 7 рабочих ракет с вероятностью 1/4?

Решение

Выберите один комплект и возьмите одну ракету из другого. Ваши шансы обзавестись хорошим комплектом с первой попытки составляют один к двум. Если вам повезло, то седьмую ракету вы возьмете из бракованной упаковки, и вероятность удачи тоже будет один к двум (три работающие ракеты из шести возможных). Поскольку в обоих случаях выбор независимый, вероятность получить семь качественных ракет составит 1/4 (1/2 1/2). Другими словами, согласно теории вероятности, 50 из 100 человек выберут хороший комплект, и еще половина из этих 50 (т.е. 25% от общего числа) возьмут хорошую ракету из оставшегося испорченного набора. Обратите внимание на то, что если в плохом комплекте находятся четыре бракованные ракеты, то только две из шести окажутся работающими, и вероятность выбрать семь хороших ракет снизится до 1/6 (1/2 1/3).

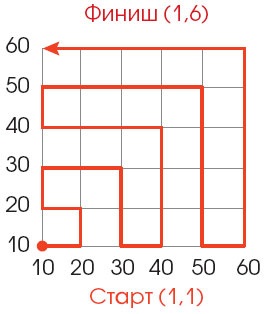
июнь 2004 № 6 "В МИРЕ НАУКИ"

Джодж Массер

Представьте себе шесть параллельных дорог, идущих с севера на юг и разнесенных с шагом 10 км, и шесть перпендикулярных им шоссе, разделенных таким же расстоянием. В местах пересечения автострад построены эстакады с въездами и съездами. Поскольку светофоры отсутствуют, повороты с одной дороги на другую осуществляются без задержек.

Попробуйте найти самые быстрые маршруты...

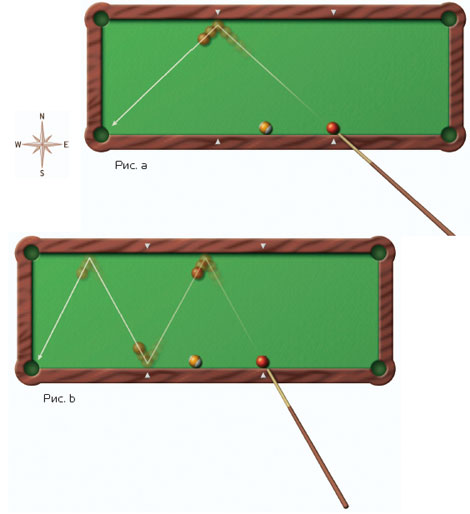
март 2003 № 3 "В МИРЕ НАУКИ"

Рис. 1. Таблица истинности для клапана И

Рис. 2. Таблица истинности для клапана ИЛИ

Дэнис Шаша

Представьте, что вы играете в пул (американский бильярд) на специальном столе размером 3х1 м. Стол спроектирован идеально: когда шар ударяется о борт, угол падения равен углу отражения. Более того, стол установлен таким образом, что его короткие стороны направлены с севера на юг, а длинные - с запада на восток. Местоположение каждого шара определяется двумя координатами (x, y), где x - расстояние на восток от юго-западного угла стола, а у - дистанция на север от той же точки. Лузы находятся только по углам стола, боковые отсутствуют.

Предположим, вы хотите положить шар из положения с координатами (2,0) в юго-западную лузу – положение (0,0), но другой шар мешает произвести прямой удар. Самый
простой способ – послать шар в противоположный борт стола, как показано на рисунке а. Нужно просто направить его на северо-запад (наклон – 1), и при попадании в точку с координатами (1,1) карамболем шар пойдет в лузу. Также легко увидеть, как можно справиться с этой задачей, используя три рикошета от бортов. Направьте шар на северо-запад (наклон – 2), как показано на рисунке b. Но прежде чем очутиться в лузе, он попадет в точки с координатами (11/2 ,1), (1,0) и (1/2,1).

Но как произвести удар, коснувшись бортов только дважды? Предположим, кто-то хочет поставить достаточно крупную сумму, полагая, что вам не удастся исполнить такой трюк. Каким должен быть наклон, чтобы попасть в лузу через два рикошета?

Один из вариантов ответа на головоломку СКОРОСТНАЯ СЕТКА

К сожалению начиная с сентября 2004 года головоломки на русском языке не публикуются. В оригинальном издании остались.