
|
|
|
|
|
|
|
|
|
Все про числаНе могу удержаться от того, Про каждое число можно рассказать что-то интересное. Каждое число чем-то отличается от других, а чем-то и похоже. На этой странице я планирую помещать описания интересных свойств (на мой взгляд, конечно) чисел.
Постоянная Капрекара
Получение: выбрать любое четырехзначное число, в котором не все циры
одинаковые. Расположить цифры сначала в порядке убывания, затем,
переставив их в обратном порядке, образовать новое число. Вычесть новое
число из старого. Повторяя этот процесс с получающимися разностями (не
более чем за семь шагов) получим число 6174 ,
которое будет затем воспроизводить самого себя. 4321 - 1234 = 3087
Возьмем теперь любое натуральное число и вычислим сумму квадратов цифр.
С полученным числом повторим операцию. Будем поступать таким же образом и
далее. Примеры: 1118 Примечание: Учитывая, что число 145 не переходит само в себя, а порождает цикл, приводящий к 145, корректнее было бы говорить про набор интересных чисел, обладающих вышеописанными свойствами: 145, 42, 20, 4, 16, 37, 58, 89 .
Числа Армстронга
А что, если вместо суммы квадратов вычислять сумму кубов цифр числа?
Оказывается, "орбиты" получаются гораздо интереснее. Некоторые числа
"вырождаются" - приходят к единице. Другие - "стабилизируются": через
несколько шагов цепочка приводит к одному из чисел 153,
370, 371 или 407 . Эти четыре числа
обладают замечательным свойством: они равны сумме кубов своих цифр.
Наконец, возможны и другие варианты концовки: например, есть цикл из двух
чисел Числа 153, 370, 371 и 407 имеют специальное название - числа Армстронга (в честь математика, который их впервые исследовал). Строгое математическое определение таково: n-значное число называется числом Армстронга, если оно равно сумме n-ых степеней своих цифр.
Самопорожденные числа(открыты Капрекаром в 1949 г.)Возьмем любое целое число и прибавим к нему сумму его
цифр. Самопорожденное число - это число, у которого нет
генератора. Самопорожденные числа:
1 000 000 - самопорожденное число.
При умножении числа 142857 на числа от 1 до 6
получается произведение, записанное теми же цифрами, переставленными в
циклическом порядке:
Что интересно, если умножить 142857 на 7, то получится число 999999. Число 142857 совпадает с периодически повторяющейся последовательностью цифр, стоящих в дробной части числа 1/7, записанного в десятичной форме.
Почти целое числоУдивительный пример того, что используя иррациональные числа, можно получить целое число с точностью до 10-13 :
Число 45 можно представить как сумму совершенно не целых слагаемых:
Заметьте, что слагаемых в этой сумме также ровно 45.
А вот просто красивый пример на умножение:
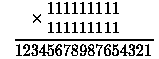 Впрочем, подобных примеров довольно много и они не менее красивы:
12345679 x 8 = 98765432
Умножение на единицуВ предыдущем примере при перемножении чисел, состоящих только из
единиц, получается число, содержащие все цифры, кроме нуля. 1 + 2 + 2 2 + ... + 2n =
Как получить любое число используя только три двойкиОчевидно проверяется, что любое число можно получить используя только три числа 2 и конечное количество математических знаков:
здесь количество знаков радикала должно быть ровно N.
Корень из двух в двоичной записиРассмотрим последовательность
Числа словамиВ этой фразе двадцать восемь букв.
Это предложение содержит двенадцать слов, двадцать шесть слогов и семьдесят три буквы.
В этой фразе два раза встречается слово "в", два раза встречается слово "этой", два раза встречается слово "фразе", четырнадцать раз встречается слово "встречается", четырнадцать раз встречается слово "слово", шесть раз встречается слово "раз", девять раз встречается слово "раза", семь раз встречается слово "два", три раза встречается слово "четырнадцать", три раза встречается слово "три", два раза встречается слово "девять", два раза встречается слово "семь", два раза встречается слово "шесть".
Девять слов назад это предложение еще не началось.
Вы только что начали читать предложение, чтение которого Вы уже заканчиваете.
Число, первая цифра которого показывает, сколько в этом числе единиц, вторая - сколько в нем двоек, третья - сколько троек, ..., десятая - сколько нулей:
Число, первая цифра которого показывает, сколько в этом числе нулей, вторая - сколько в нем единиц, третья - сколько двоек и т.д.:
Логическое противоречиеТо, что написано на этой странице неправда!
Закон экономикиПри снижении цены на 20%, количество товара покупаемого на одно и то же количество денег возрастает на 25%.
"Золотое сечение", записанное в виде цепной дробиКак получить что-то иррациональное используя только единицы:
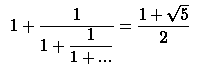
Куда ни читай, а все квадрат получается (да и квадрат-то тоже можно в любую сторону читать)
РепьюнитыЧисло называется репьюнитом, если оно составлено из одних единиц.
Например, Известно пять простых репьюнитов: R2, R19, R23, R317 и R1031, причем, что самое интересное - индексы этих репьюнитов также простые числа.
Числа СмитаЧисло называется числом Смита, если сумма цифр числа равна сумме цифр разложения этого числа на простые множители. Например:
Числа Смита: 4, 22, 27, ... На интервале (0, 10 000) - 376 чисел Смита Известно также родственное понятию числа Смита, понятие Братья Смита - это числа Смита стоящие рядом друг с другом. Например, (728 ; 729 ) или (2964 ; 2965 ). Однако неизвестно сколько существует таких пар.
Числа ФибоначчиЧисло называется числом Фибоначчи, если оно является одним из членов последовательности:
Однако не все знают, что (n+1)-й член ряда Фибоначчи можно получить, вычислив определитель матрицы размером (n x n):
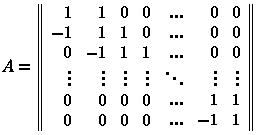 Можно также определить n-й член ряда Фибоначчи, непосредственно подсчитав выражение:
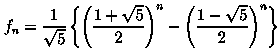
Очевидно, что из любого числа можно получить 0 или 1 , применив к этому числу функцию Дирихле:
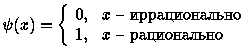 Не очевидно, что саму функцию Дирихле можно записать в аналитическом виде:
"Неправильные" вычисления иногда бывают правильными
Примеры:
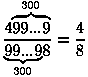
Пример:
Пример:
Красивое разложение корня четвертой степени из числа 399550 :
Число 3 получается из забавной формулы:
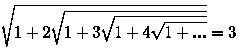 Эта формула является следствием более общей формулы при n=1:
Очень похоже (и так же красиво) выглядит запись числа 4 :
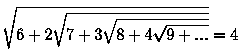 Это также следствие более общей формулы при n=1:
Максимальное число, которое можно построить из трех троек без использования математических знаков - 333 , а максимальное число, которое можно построить из трех четверок без использования математических знаков - 4( 44 )
Развивая начатую тему: наибольшее число, которое можно записать с помощью трех единиц без использования математических знаков - 111 ; наибольшее число, которое можно записать с помощью четырех единиц без использования математических знаков - 1111 ; наибольшее число, записанное тремя цифрами без использования математических знаков - 9( 99 ) .
Несколько утверждений про числаЛюбое нечетное число можно представить в виде разности квадратов двух
чисел. 23 = 144 - 121
Любое натуральное число, кратное 4, можно представить в виде разности
квадратов двух чисел. 44 = 144 - 100
Любое натуральное число, дающее в остатке 1 при делении на 4, можно представить в виде суммы двух квадратов.
45 = 36 + 9
Если сумма двух целых чисел - число, оканчивающееся нулем, то квадраты
этих чисел оканчиваются одной и той же цифрой. 4 + 6 = 10
Числа, сумма, произведение и частное которых равны между собой: 0,5 и -1 .
Пи - число иррациональное, однако его можно вычислить достаточно
простым способом, используя всевозможные ряды, произведения и т.п.
Или так: 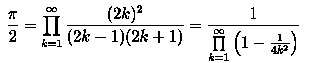 Или так:
Для совсем эстетов предлагается следующий способ: вычисляется число е, затем из приведенной ниже формулы выражается Пи (кстати, формулу придумал и доказал Рамануджан):
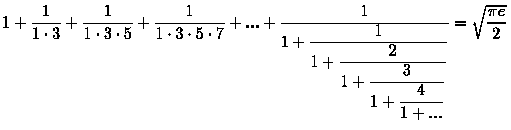
Про простые числа можно говорить бесконечно (не в том смысле, что самих простых чисел бесконечно много и было бы просто тривиально начать их перечислять, а в смысле, что у простых чисел очень много интересных свойств).
Известна, например, теорема П. Л. Чебышева, что между двумя натуральными числами n и 2n имеется по крайней мере одно простое число.
Вот список всех простых чисел от 0 до 2000: 1 2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97 101 103 107 109 113 127 131 137 139 149 151 157 163 167 173 179 181 191 193 197 199 211 223 227 229 233 239 241 251 257 263 269 271 277 281 283 293 307 311 313 317 331 337 347 349 353 359 367 373 379 383 389 397 401 409 419 421 431 433 439 443 449 457 461 463 467 479 487 491 499 503 509 521 523 541 547 557 563 569 571 577 587 593 599 601 607 613 617 619 631 641 643 647 653 659 661 673 677 683 691 701 709 719 727 733 739 743 751 757 761 769 773 787 797 809 811 821 823 827 829 839 853 857 859 863 877 881 883 887 907 911 919 929 937 941 947 953 967 971 977 983 991 997 1009 1013 1019 1021 1031 1033 1039 1049 1051 1061 1063 1069 1087 1091 1093 1097 1103 1109 1117 1123 1129 1151 1153 1163 1171 1181 1187 1193 1201 1213 1217 1223 1229 1231 1237 1249 1259 1277 1279 1283 1289 1291 1297 1301 1303 1307 1319 1321 1327 1361 1367 1373 1381 1399 1409 1423 1427 1429 1433 1439 1447 1451 1453 1459 1471 1481 1483 1487 1489 1493 1499 1511 1523 1531 1543 1549 1553 1559 1567 1571 1579 1583 1597 1601 1607 1609 1613 1619 1621 1627 1637 1657 1663 1667 1669 1693 1697 1699 1709 1721 1723 1733 1741 1747 1753 1759 1777 1783 1787 1789 1801 1811 1823 1831 1847 1861 1867 1871 1873 1877 1879 1889 1901 1907 1913 1931 1933 1949 1951 1973 1979 1987 1993 1997 1999
Принимаются замечания, дополнения, исправления. Присылайте файлы в формате MS WORD или TeX Алексею Амилющенко. В письме либо укажите доказательство, либо ссылку на источник, где оно было опубликованно.
Приведенные выше опыты с числами были описаны в следующих
печатных изданиях: журнале "Техника-Молодежи", журнале "Scientific
American", газетах "Пионерская правда" и "Неделя", журнале "Квант", а
также в учебнике В. А. Зорича "Математический анализ", в
задачнике по функциональному анализу Кириллова и Гвишиани, в замечательных
книгах М. Гарднера ("От мозаик Пенроуза к надежным шифрам",
"Путешествие во времени" и др.), в книге "Киевские математические
олимпиады", в книгах Г. Штейнгауза ("Математический калейдоскоп" и
"Сто задач"), в книге Ф. Ф. Нагибина и Е. С. Кузьмина
"Математическая шкатулка", в весьма веселой книге "Физики все еще шутят",
а также в еженедельнике "Компьютерра" (#25 от 23 июня 1997
г.) Я выражаю свою искреннюю благодарность Константину Кнопу ("Компьютерра") за интересное содержательное общение, идеи, исправления ошибок. Я выражаю свою искреннюю благодарность Дмитрию Новикову за добавление новых числовых соотношений и исправление ошибок. Я выражаю свою искреннюю благодарность Алексею Федотову за добавление новых числовых соотношений и исправление ошибок. Я благодарен Егору Быковскому за добавление в коллекцию четных и нечетных дат. Числа и датыВ феврале 2000 года случилась заменательная дата - 02.02.2000. В записи даты - только четные цифры. Последний раз такое событие произшло 28.08.888. Последний прожитый нами нечетный день был 19.11.1999. Следующий будет 01.01.3111. Цифр вообще можно набрать прелюбопытных вволю. Если, скажем, обратиться к двоичному счислению, то 1111.111.11111111111 1111:11111:11111 это 15:31:31 15 июля 2047 года.
Число 13452Число 13452 образовано из пяти последовательных цифр (расположенных не
по порядку) так, что число образованное первыми двумя цифрами, умноженное
на среднюю цифру, дает число, образованное последними двумя цифрами.
Число 947658Число 947658 образовано из шести последовательных цифр (расположенных
не по порядку) так, что число образованное первыми двумя цифрами,
умноженное на среднюю цифру, дает число, образованное последними тремя
цифрами.
Числа 39157 и 57139Данные числа составлены из пяти первых нечетных чисел 1, 3, 5, 7 и 9
следующим образом: произведение числа, образованного из первых двух цифр,
на число, образованное двумя последними цифрами, минус число стоящее в
середине равно числу, составленному из повторений одной и той же
цифры.
Число 14441444 - наименьший квадрат целого числа, оканчивающийся наиболее длинной
последовательностью одинаковых цифр. Нуль не считается допустимой
цифрой.
Число 273863Наибольшее число, которое при умножении на 365 дает число, содержащее
восемь цифр, из которых первые четыре дважды повторяются.
Аналогичные примеры есть
но 273863 - наибольшее, удовлетворяющее условию.
Легкое деление: чтобы разделить, просто перенесите первую цифру в конецЧастное, получающееся при перестановке в конец первой цифры делимого, можно найти для любого делителя и любой. Ниже два примера.
Число 8101265822784Чтобы разделить 8 101 265 822 784 на 8, достаточно переставить первую цифру числа в конец.
Число 7101449275362318840579Чтобы разделить 7 101 449 275 362 318 840 579 на 7, достаточно переставить первую цифру числа в конец.
Легкое деление (вариант 2): чтобы разделить, просто переставьте последнюю цифру в началоВ отличие от предыдущего случая, в данном варианте решение существует не всегда. Так, например, для делителя 2 решения не существует. Однако не все так плохо.
Числа 857142 и 428571Чтобы разделить 857142 или 428571 на 3, достаточно переставить последнюю цифру каждого из чисел в начало.
Цифровые совпаденияПроизведение и сумма некоторых чисел дает в результате числа, состоящие из одинаковых цифр:
2 х 47 = 94 49 = 2 + 47; 3 х 24 = 72 27 = 3 + 24; 2 х 497 = 994 499 = 2 + 497; 2 х 263 = 526 265 = 2 + 263. Вообще, вводя девятки после первой цифры чисел из двух последних примеров, можно получить минимум два аналогичных результата при любом желаемом числе цифр:
2 х 2963 = 5926 2965 = 2 + 2963.
Квадраты-палиндромыКвадраты некоторых целых чисел можно читать как обычным образом, так и
справа налево. Некоторые из них найти очень легко. Например, квадраты
чисел 1, 11, 111 и 1111 равны соответственно 1, 121, 12 321, 1 234 321.
Все получившиеся числа - палиндромы, и данное правило применимо к любому
числу единиц, не превосходящему 9. Однако существуют и другие случаи,
которые вполне можно назвать нерегулярными.
Во всех приведенных выше примерах число цифр квадрата было нечетным. Квадрат числа 836, равный 698 896, содержит четное число цифр. Среди всех квадратов, содержащих данное четное число цифр, палиндромический квадрат наименьший.
Число 1234567890Число 1 234 567 890 разлагается на множители следующим образом:
Задача о десяти цифрахСуществует четыре числа, составленных из всех десяти цифр, таким образом, что эти числа делятся на все числа от 2 до 18:
3 785 942 160; 4 753 869 120; 4 876 391 520.
Число 3333377733Наименьшее число, которое записывается только с помощью цифр 3 и 7, и при этом обладает следующим свойством: само число и сумма его цифр делится на 3 и 7 - число 3 333 377 733.
Извлечение кубического корняИногда, чтобы извлечь кубический корень из числа, достаточно посчитать сумму цифр этого числа. Ниже приведены все такие числа:
512 - сумма цифр числа равна 8, а 8 3 = 512; 4913 - сумма цифр числа равна 17, а 17 3 = 4913; 5832 - сумма цифр числа равна 18, а 18 3 = 5832; 17 576 - сумма цифр числа равна 26, а 26 3 = 17 576; 19 683 - сумма цифр числа равна 27, а 27 3 = 19 683.
Три различные цифрыЧисла, составленные из трех различных цифр, каждое из которых делится на квадрат суммы своих цифр:
243 делится на 81 = (2 + 4 + 3)2 ; 324 делится на 81 = (3 + 2 + 4)2 ; 392 делится на 196 = (3 + 9 + 2)2 ; 405 делится на 81 = (4 + 0 + 5)2 ; 512 делится на 64 = (5 + 1 + 2)2 ; 605 делится на 121 = (6 + 0 + 5)2 ; 648 делится на 324 = (6 + 4 + 8)2 ; 810 делится на 81 = (8 + 1 + 0)2 ; 972 делится на 324 = (9 + 7 + 2)2 .
В обратном порядкеПроизведение чисел 123 456 789 и 989 010 989 равно 122 100 120 987 654 321. Что интересно, в девяти младших разрядах полученного числа стоят цифры 9, 8, 7, 6, 5, 4, 3, 2, 1 (именно в таком порядке).
Арифметическая прогрессияРассмотрим все цифры кроме нуля (1, 2, 3, 4, 5, 6, 7, 8, 9) и разобьем
их на три группы таким образом, что полученные числа представляют из себя
арифметическую прогрессию. Существует как минимум четыре способа проделать вышеописанную операцию, чтобы в каждом случае три числа образовывали арифметическую прогрессию, а среднее число оставалось одним и тем же:
291 564 837; 237 564 891; 231 564 897, где разность равна соответственно 267, 273, 327 и 333. В. Тебо в книге "Parmi les Nombers Curieux" показал, что существует 760 таких прогрессий. Кроме числа 456 (и его перестановок), среднее число может быть любой перестановкой следующих групп их трех цифр: 258, 267, 348 и 357.
Число 201599999798400Число 201 599 999 798 400 представляет из себя сумму всех чисел, которые можно составить из девяти цифр (0 исключен), используя каждую цифру в каждом числе один и только один раз.
Число 1026753849Число 1 026 753 849 - наименьший квадрат, содержащий все десять цифр от 0 до 9, причем каждую цифру - лишь по одному разу.
Число 9814072356Число 9 814 072 356 - наибольший квадрат, содержащий все десять цифр от 0 до 9, причем каждую цифру - лишь по одному разу.
Числа 567 и 854Данные числа и только они содержат вместе со своими квадратами по одному и только одному разу каждую из девяти цифр, исключая нуль.
8542 = 729 316.
Число 207Используя каждую из девяти цифр, исключая нуль, один и только один раз, составим простые числа таким образом, что сумма этих чисел была минимальной. Эта сумма равна 207.
Девять цифр до и после знака равенстваЕсли 32 547 891 умножить на 6 (таким образом, в данной операции использованы все девять цифр от 1 до 9), то получится произведение, равное 195 287 346, также содержащее девять цифр по одному разу. Еще примеры такого рода:
89 745 321 х 6 = 538 471 926; 98 745 231 х 6 = 592 471 386.
Сложение и умножение дает одинаковый результатСуществуют пары чисел, которые при сложении и умножении дают одинаковый результат, например: 1,1 и 11.
Впрочем, подобных чисел бесконечно много:
6 + 1,2 = 6 х 1,2 = 7,2; 26 + 1,04 = 26 х 1,04 = 27,04. Вообще, для любого n парное ему число m, удовлетворяющее описанному свойству, можно вычислить по формуле
Квадраты и кубыДва наименьших числа, таких что разность их квадратов представляет собой куб, а разность кубов - квадрат: 10 и 6.
10 3 - 6 3 = 1000 - 216 = 784 = 282 .
Числа, равные сумме кубов своих цифрСуществуют четыре числа, если не считать 1, совпадающие с суммой кубов своих цифр:
370 = 27 + 343; 371 = 27 + 343 + 1; 407 = 64 + 343.
Составные квадратыСуществует только два трехзначных квадрата (без нулей), которые, будучи выписанными подряд, образуют шестизначное число, в свою очередь представляющее собой квадрат:
225 625 = 475 2
Число 2519Число 2519 таково, что если разделить его на 2, то в остатке получится 1; если разделить на 3, то в остатке получится 2; если разделить на 4, то в остатке получится 3; если разделить на 5, то в остатке получится 4; если разделить на 6, то в остатке получится 5; если разделить на 7, то в остатке получится 6; если разделить на 8, то в остатке получится 7; если разделить на 9, то в остатке получится 8; если разделить на 10, то в остатке получится 9:
2519 = 839 х 3 + 2; 2519 = 629 х 4 + 3; 2519 = 503 х 5 + 4; 2519 = 419 х 6 + 5; 2519 = 359 х 7 + 6; 2519 = 314 х 8 + 7; 2519 = 279 х 9 + 8; 2519 = 251 х 10 + 9.
Двойная последовательностьДля некоторых натуральных чисел n можно построить
последовательность, в которой каждое их чисел 1, 2, 3, ..., n
встречается дважды, причем второе появление каждого из чисел r
происходит на r-м месте после его первого появления.
для n = 5 имеем: 3, 5, 2, 3, 2, 4, 5, 1, 1, 4; для n = 8 имеем: 8, 6, 4, 2, 7, 2, 4, 6, 8, 3, 5, 7, 3, 1, 1, 5. Такая последовательность не существует, если остаток числа n при делении на 4 равен 2 или 3.
a b и baЧасто, бывает нетрудно определить, что больше: ab или b a . Очевидно, что
Однако потребуется некоторые усилия, чтобы доказать, что
Число 40500000001Сумма всех цифр, используемых при записи всех чисел, первое из которых единица, а последнее миллиард, составляет 40 500 000 001.
Простые числа и арифметическая прогрессияСуществуют арифметические прогрессии, где несколько последовательных членов прогрессии являются к тому же еще и простыми числами. Например, 10 последовательных членов арифметической прогрессии
являются простыми числами, так же как и 13 членов
все являются простыми числами. Если рассматривать арифметические прогрессии с разностью 6, единственный случай, когда в такой прогрессии пять последовательных чисел:
Можно также доказать, что в любой арифметической прогрессии из натуральных чисел с разностью, меньшей 2000, не может находиться 12 последовательных простых чисел.
Числа 49, 4489, 444889, 44448889 и т.д.Каждый член последовательности
является точным квадратом.
Число 4 и система неравенств4 - наибольшее целое число n, для которого существует число x, одновременно удовлетворяющее неравенствам k < x k < k + 1 (k = 1, 2, 3, ..., n),
2 < x2 < 3, 3 < x3 < 4, 4 < x4 < 5, . . . . . При этом x может принимать любое значение между
Всегда квадратПусть четное количество единиц, записанных друг за другом, образуют число A, а вдвое меньшее количество четверок - число B. Тогда число A + B + 1 всегда является полным квадратом.
1111 + 44 + 1 = 1156 = 34 2 , 111111 + 444 + 1 = 111556 = 3342 , . . . . .
Любопытное свойство числа 3Если m и n - два натуральных числа, то одно из чисел
Группировка натуральных чиселПредположим, что натуральные числа разделены на группы следующим образом:
и что каждая вторая группа отброшена. Тогда сумма чисел в первых
k оставшихся группах всегда равна k4 .
Необыкновенное свойство комплексных чиселДля x = 1 + i
Можно обобщить этот факт на более общий случай. При указанном выборе чисел x, y и z равенство
справедливо для всех простых чисел p > 3. Литература
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Автор | )c( 2000-2019 Kопирайта нет, копируйте на здоровье :) 100112 лет в Интернете |
|