Лента Мёбиуса
Вариации на старую тему

Д. Фукс

Я не буду предлагать вам водить по ленте Мёбиуса пальцем или разрезать её по средней линии. Речь пойдёт о вещах, менее известных. Начну с вопроса:

Ожидаемый ответ: полоска должна быть узкой и длинной, с возможно бóльшим отношением длины к ширине. Скажем, из квадратного листа ленты Мёбиуса не сделаешь.

Это верно, но с одной оговоркой, которую легко недооценить: ограничения на размер имеют значение лишь в том случае, когда бумагу запрещается  мять. Если же мять бумагу не запрещается, то ленту Мёбиуса можно склеить не только из квадрата, но из прямоугольника любых размеров» – склеиваемые стороны могут быть даже во сколько угодно раз длиннее несклеиваемых.

Сделать это можно так (рис. 1). Сложим прямоугольный лист в гармошку, перегнув его  чётное  число раз. Затем из этой гармошки, как из толстой бумажной полоски, склеим ленту Мёбиуса, вставляя соответствующие части гармошки друг в друга. Из рисунка 1 видно, что лист бумаги, из которого склеена лента Мёбиуса, оказался смятым.

Рис. 1

Предположим теперь, что бумажную полоску можно  изгибать, но не мять. Примем ширину полоски за единицу. Ясно, что чем длиннее полоска, тем легче склеить из неё ленту Мёбиуса. Таким образом, существует такое число λ, что из полоски длины больше λ ленту Мёбиуса склеить можно, а из полоски длины меньше λ – нельзя (что будет для полоски, длина которой в точности равна λ, нас не интересует). Очень хотелось бы найти это λ.

Удивительно, но решение этой задачи до сих пор не известно.

Здесь я докажу для λ неравенства

(при этом наличием склеиваемых участков полоски мы пренебрегаем: предполагается, что края полоски склеиваются встык) и постараюсь объяснить, почему не удаётся вычислить λ точнее.

Раз требование не мять бумагу так важно, посмотрим, каков его математический смысл.

Легко понять, что запрещение мять бумагу значительно ограничивает возможность манипулировать бумажным листом. Например, лист бумаги, не помяв, можно свернуть в трубку или сложить  без складки  пополам, но нельзя сложить вчетверо (рис. 2). Из листа бумаги, не смяв его, можно сделать конус («фунтик»), но нельзя сделать сферу или даже её кусочек (рис. 3): прижмите лист бумаги к глобусу, и обязательно появятся складки. Как видно, листу бумаги можно придать далеко не всякую форму.

Рис. 2

Рис. 3

Поверхности, которые можно сделать из листа бумаги, изгибая, но не сминая его, математики называют развёртывающимися. (Примеры развёртывающихся поверхностей показаны на рисунке 4.) Конечно, в математике развёртывающиеся поверхности определяются не так: в математическом языке отсутствуют слова «бумага», «сминать», «сделать». Существует целая теория развёртывающихся поверхностей, среди достижений которой – удовлетворительный ответ на вопрос, какими они могут быть; математики называют это «классификацией» (ответ принадлежит Леонарду Эйлеру). Я не собираюсь здесь излагать общую теорию развёртывающихся поверхностей: всякая общая теория скучновата. Я приведу только некоторые свойства развёртывающихся поверхностей, нужные для дальнейшего. Наше наглядное определение не позволяет их доказать, так что придётся рассматривать эти свойства как экспериментальные факты (возьмите лист бумаги и убедитесь в их справедливости).

Рис. 4

1. Через каждую точку A развёртывающейся поверхности, не лежащую на её границе, проходит лежащий на поверхности отрезок, не кончающийся в A. Иначе говоря, в каждой точке к развёртывающейся поверхности (изогнутому, но не смятому листу бумаги) можно приложить спицу так, чтобы она прилегала к поверхности на некотором протяжении по обе стороны от взятой точки. Такой отрезок называется образующей поверхности (условимся, что это название относится только к отрезкам максимальной длины, целиком лежащим на поверхности, то есть, к отрезкам, не содержащимся в бóльших отрезках с этим свойством).

2. Если через точку A, не лежащую на границе поверхности, проходят две различные образующие, причём A не является концом ни одной из них, то достаточно маленький кусок поверхности, окружающий A, является плоским. В таком случае точку A мы будем называть плоской.

3. Если точка A, не лежащая на границе поверхности, является концом какой-нибудь образующей, скажем, a, то окрестность точки A устроена так. Через точку A проходит единственная не кончающаяся в ней образующая, скажем, b (рис. 5). Эта образующая разделяет поверхность на две части. С той стороны от образующей b, с которой находится образующая a, к образующей b прилегает плоский кусок, с другой стороны от b, сколь угодно близко от точки A, имеются не плоские точки. Точку A в этой ситуации мы будем называть полуплоской.

Рис. 5

а) Рис. 6 б)

Подчеркнём, что если точка поверхности не является ни граничной, ни плоской, то через неё проходит единственная не кончающаяся в ней образующая, причём концы этой образующей лежат на границе поверхности.

Примеры. Лист бумаги, свёрнутый в трубочку или в фунтик, плоских (и полуплоских) точек не имеет. У трубочки образующие составляют семейство параллельных отрезков, у фунтика – семейство отрезков, веером расходящихся из одной точки. Возможны более сложные расположения образующих. Например, образующие и плоские точки развертывающейся поверхности, изображённой на рисунке 6а, показаны на рисунке 6б (на нём поверхность развёрнута в плоский лист бумаги): тонкие синие линии – образующие, а закрашенные области состоят из плоских точек.

Точки, лежащие на границе области плоских точек, являются либо граничными для всей поверхности, либо полуплоскими. Если поверхность сделана из бумажного многоугольника (скажем, из прямоугольника), то плоские точки составляют один или несколько плоских многоугольников, причём у каждого из этих многоугольников вершины лежат на границе поверхности, а стороны либо лежат на границе, либо состоят из полуплоских точек (см. ещё раз рисунок 6б).

Упражнение 1. Развёртывающаяся поверхность сделана из а) квадратного листа со стороной 1; б) круга диаметра 1. Докажите, что хотя бы одна из её образующих имеет длину не меньше а) 1; б) √3/2.

Вернёмся к нашему основному сюжету: вычислению λ – нижней грани длин бумажных полосок ширины 1, из которых можно склеить несмятую ленту Мёбиуса.

Доказательство. Пусть лента Мёбиуса сделана из бумажной полоски длины l. Намотаем на неё длинную бумажную ленту. Эта лента (толщиной бумаги пренебрегаем) будет составлена из прямоугольников одинаковой длины, каждый из которых принимает форму нашей ленты Мёбиуса. Отметим на длинной ленте прямолинейные образующие и плоские точки (как на рисунке 6б). Получится что-то вроде рисунка 7. Картина периодична: всё повторяется с периодом, равным 2l. Можно сказать больше: при сдвиге влево или вправо на l картинка меняется, но строго определённым образом; именно, она переворачивается (т.е. зеркально отражается в средней линии полоски). Области плоских точек представляют собой четырёхугольники (которые могут выродиться в треугольники), ограниченные двумя отрезками противоположных краёв ленты и двумя отрезками, проходящими по ленте. Части ленты, не попавшие в эти области, вымощены образующими, концы которых лежат на краях ленты. (Всё это следует из свойств 1-3 развёртывающихся поверхностей, приведённых в п. 2.) Плоские участки также можно вымостить образующими, так что вся лента будет покрыта непрерывным семейством образующих (рис. 8). Образующие в одинаковых четырёхугольниках можно выбирать одинаковым образом, так что описанная выше периодичность сохранится.

Возьмём любую образующую из нашего семейства, скажем, [AB]. Если симметрично отразить её в средней линии полоски и затем перенести в любую сторону (скажем, вправо) на l, то получится отрезок CD, который тоже является образующей из нашего семейства (рис. 9). Заметим (это важно), что |AC| + |BD| = 2l. При наматывании нашей длинной ленты на ленту Мёбиуса образующие [AB] и [CD] займут одинаковое положение, причём точка A совместится с D, а точка B – с C; другими словами, отрезки AB и CD составят в пространстве угол в 180°. Между [AB] и [CD] располагается непрерывное семейство образующих. При движении от [AB] к [CD] величина угла, который эти образующие составляют в пространстве с [AB], непрерывно изменяется от 0° до 180°. (Напомним, что величина угла между отрезками KL и MP в пространстве определяется как ÐKLQ, где Q – такая точка, что отрезки LQ и MP равны по длине, параллельны и направлены в одну сторону.)

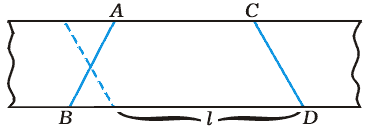Рис. 9	Рис. 11
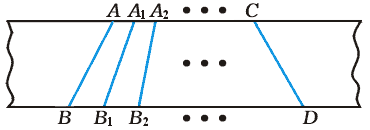Рис. 10

Возьмём любое n и найдём между [AB] и [CD] такие образующие [A₁B₁], ..., [A_n–1B_n–1], что величина угла между [AB] и [A_kB_k] равна k·180°/n (точки A₁, ..., A_n–1 в этом порядке лежат между A и C, а точки B₁, ..., B_n–1 в этом порядке лежат между B и D; см. рис. 10). Длина каждой из образующих больше или равна 1, а величина угла между пространственными положениями двух соседних образующих не меньше 180°/n. Покажем, что каждая из сумм |AA₁| + |BB₁|, |A₁A₂| + |B₁B₂|, ..., |A_n–1C| + |B_n–1D| не меньше длины a_2n стороны правильного 2n-угольника, вписанного в окружность радиуса 1. Это видно из рисунка 11. На этом рисунке отрезки A_kE и A_k+1B_k+1 равны по длине, параллельны и направлены в одну сторону, |A_kF| = |A_kH| = 1 и [FG] || [EB_k] (рисунок 11 сделан в предположении, что |A_k+1B_k+1| < |A_kB_k|; изменения, необходимые в случаях |A_k+1B_k+1| = |A_kB_k| и |A_k+1B_k+1| > |A_kB_k|, очевидны). Мы видим, что |A_kA_k+1| + |B_kB_k+1| = |EB_k+1| + |B_kB_k+1| ≥ |EB_k| ≥ |FG| ≥ |FH| ≥ a_2n (здесь |A_kA_k+1|, |B_kB_k+1|, |EB_k+1| – длины изображённых на рисунке 11  криволинейных  отрезков; эти длины совпадают с длинами отрезков [A_kA_k+1], [B_kB_k+1] рисунка 10; предпоследнее неравенство следует из того, что ÐFHG > 90°, а последнее – из того, что ÐFA_kH ≥ 180°/n).

Итак, 2l = |AC| + |BD| = (|AA₁| + |BB₁|) + (|A₁A₂| + |B₁B₂|) + ... + (|A_n–1C| + |B_n–1D|) ≥ na_2n, т.е. 2l  при любом  n не меньше половины периметра правильного 2n-угольника, вписанного в окружность радиуса 1. Значит, 2l не меньше половины длины самой этой окружности, то есть π, и l ≥ π/2. Теорема доказана.

Эта теорема проще предыдущей: для её доказательства достаточно объяснить, как склеить ленту Мёбиуса из полоски, длина которой больше √3. Предположим сначала, что её длина в точности равна √3. Тогда на этой полоске можно расположить два правильных треугольника (рис. 12). Перегнём полоску по боковым сторонам этих треугольников, чередуя направления сгиба (рис. 13; возьмите ножницы и бумагу и проделайте это). Края AB и CD полоски совместятся, причём точка A совместится с точкой D, а точка B – с точкой C. Получится лента Мёбиуса.

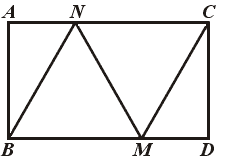Рис. 12	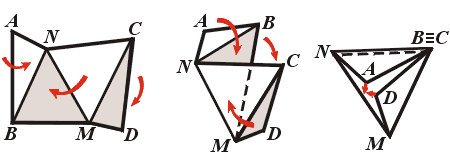Рис. 13
Рис. 14	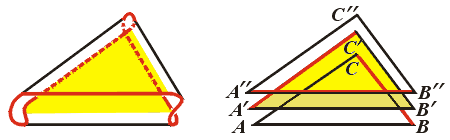Рис. 15

При этом построении было нарушено главное правило – не мять бумагу. Но легко понять, что если длина полоски хоть немного больше √3, то  излом  по образующей можно заменить  изгибанием, производимым на узком участке (рис. 14). Короче говоря, излом вдоль прямолинейного отрезка нам не страшен: его можно заменить близким к нему изгибанием. (Непоправимое сминание бумаги происходит, когда две линии перегиба пересекаются, т.е. когда лист складывается наподобие носового платка – всё это известно нам из повседневного опыта.)

Как выглядит получившаяся лента Мёбиуса, показано на рисунке 15. Её устройство можно представить себе так: три одинаковых правильных треугольника ABC, A'B'C', A"B"C" лежат параллельно друг другу, соответствующие вершины над соответствующими вершинами; стороны AB и A'B', B'C' и B"C", C"A" и CA соединены перемычками. Линия склейки проходит по медиане одного из треугольников.

Упражнение 2. Нарисуйте для ленты Мёбиуса, построенной в доказательстве теоремы 2, схему прямолинейных образующих и плоских точек (подобно рисунку 7).

Пока задача не решена, трудно сказать,  почему  она не решена. Всё же иногда в разных нерешённых задачах удаётся проследить общие трудности, отметить, так сказать, на математической карте труднопроходимые места, что позволяет подчас предсказать успех или неудачу при решении той или иной задачи.

В предыдущем параграфе мы доказали, что λ есть одна из точек отрезка [π/2; √3]. Какая же? Может быть, на этот счёт можно высказать хотя бы правдоподобную гипотезу? Я думаю, что λ = √3, и меня не удивляет, что доказать этого не удаётся.

Дело вот в чём. Доказательство теоремы 1 оставляет неиспользованным одно важное свойство нашей ленты Мёбиуса – отсутствие у неё самопересечений. Самопересекающуюся ленту нельзя сделать из бумаги, но представить себе её можно: подобно самопересекающейся линии на плоскости она «проходит сквозь себя», причём можно разделить её на части, каждая из которых самопересечений не имеет.

Допустим, что, говоря о бумажных лентах Мёбиуса, мы с самого начала разрешили им иметь самопересечения. Тогда λ приобретает новый смысл, – новое значение λ будет меньше прежнего или равно ему. При этом теорема 1 останется верной, и в её доказательстве не придётся менять ни одного слова: отсутствие самопересечений в этом доказательстве нигде не используется. Что же касается теоремы 2, то, если разрешены самопересечения, её можно значительно улучшить. Именно:

Теорема 3. Ленту Мёбиуса с самопересечениями можно склеить из полоски любой длины, большей π/2.

Делается это так. Возьмём достаточно большое нечётное n и построим правильный n-угольник, вписанный в окружность диаметра 1. Рассмотрим, далее, n содержащих центр окружности треугольников, каждый из которых ограничен стороной и двумя диагоналями n-угольника (рис. 16; здесь n=7). Эти треугольники покрывают наш n-угольник, некоторые его места – по нескольку раз. Приложим теперь эти n треугольников друг к другу так, как показано на рисунке 17, после чего отрежем по длинной медиане половину самого левого треугольника и приложим её к самому правому треугольнику (рис. 17). Получится прямоугольная полоска с отношением длины к ширине, бóльшим π/2 и стремящимся к π/2 при n, стремящимся к ∞ (ширина полоски стремится к 1, а длина – к π/2). Если последовательно перегнуть эту полоску по всем проведённым на ней линиям, чередуя направления сгиба (рис. 18), то треугольники расположатся как на рисунке 16 (возьмите ещё раз ножницы и бумагу и проделайте это). Отрезки AB и CD при этом почти совместятся – между ними окажется только несколько слоёв сложенной бумаги. При этом «почти совмещении» точка A совместится с D, а точка B – с C, так что если бы мы смогли «пропустить ленту сквозь себя» и склеить |AB| с |CD|, то получилась бы лента Мёбиуса. Если ленту взять чуть более длинной, можно избежать складок, подобно тому как мы это сделали в доказательстве теоремы 2. Что получится, я попробовал изобразить на рисунке 19.

Рис. 16	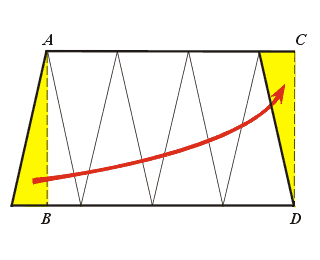Рис. 17
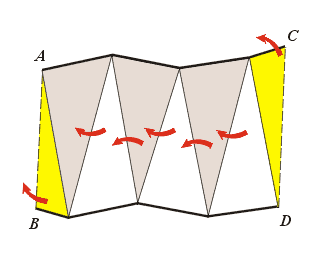Рис. 18	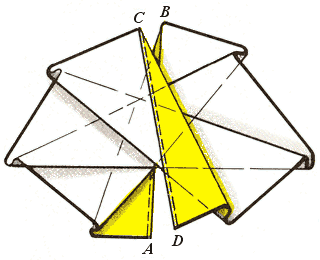Рис. 19

Упражнение 3. Нарисуйте для ленты Мёбиуса, изображённой на рисунке 19, диаграмму плоских точек и прямолинейных образующих.

Таким образом, если бы мы захотели (для лент без самопересечений) доказать, что λ ≥ μ, где μ > √3, нам пришлось бы в доказательстве обязательно учитывать отсутствие самопересечений. Наличие или отсутствие самопересечений у той или иной фигуры в трёхмерном пространстве – это задача «трёхмерной геометрии расположения». Весь опыт математики показывает, что задачи о расположении в трёхмерном пространстве очень трудны. Ведь эта геометрия включает в себя, скажем, теорию узлов и зацеплений, известную своей неприступностью («Квант», 1975, № 7, с. 6); в ней возможны такие феномены как «рогатая сфера Александера» («Квант», 1977, № 7, с. 22); простейшие её вопросы, например, можно ли через маленькую дырку вывернуть наизнанку тор, – ставят в тупик нашу интуицию. И вот что удивительно. Казалось бы, в пространствах размерности больше трёх проблемы расположения должны стоять ещё более остро. Но нет: с ростом размерности эти трудности сглаживаются. Впрочем, «сглаживание» начинается с размерности 5; четырёхмерное пространство в известном смысле не проще трёхмерного. К сожалению, здесь я не могу аргументировать только что сказанное, так что прошу поверить мне на слово.

Но вернёмся к ленте Мёбиуса. Теорема 1, как мы видели, в действительности относится к самопересекающимся лентам. Маловероятно, чтобы условие отсутствия самопересечений не воздействовало на λ; однако учесть это воздействие не удаётся, поскольку математика не обладает достаточными техническими средствами для изучения самопересечений в трёхмерном пространстве. Напротив, вполне вероятно, что теорема 2  неулучшаема. Ведь улучшить её – значит придумать новую  конструкцию  ленты. Опыт показывает, что оптимальные конструкции бывают простыми и гармоничными, каковой и является конструкция из доказательства теоремы 2. Естественно предположить, что если бы лучшая конструкция существовала, она была бы найдена – за столько лет!

Вот почему можно ожидать, что λ = √3.

Склеим из бумажной полоски не ленту Мёбиуса, а цилиндр (размеры полоски – любые). Можно ли, не сминая бумаги, вывернуть цилиндр наизнанку? Если цилиндр широк и низок, то, конечно, можно, а если он узок и высок – то нельзя. Обозначим через σ такое число, что если отношение длины полоски к ширине больше σ, то цилиндр вывернуть можно, а если меньше – то нельзя. Доказательства трёх следующих теорем (более трудных, чем теоремы 1, 2, 3) я оставляю вам в качестве задачи:

Теорема 1'. σ ≥ π.

Теорема 2'. σ ≤ π + 2.

Теорема 3'. Предположим, что в процессе выворачивания допускаются самопересечения. Тогда любой цилиндр, сделанный из полоски, у которой отношение длины к ширине больше π, можно вывернуть наизнанку (не сминая бумаги).

Больше ничего об этом не известно.

В заключение я хочу сказать, что мысль написать эту статью возникла у меня при чтении статьи Б. Гальперина и К. Уивера в журнале «Transactions of the American Mathematical Society» (1977, т. 230), из которой я узнал о современном положении дел с обсуждавшимися проблемами.