Математические развлечения в Сети

Константин Кноп

Problem of the …

Начнем обзор сетевых ресурсов для любителей математики с небольшой подборки англоязычных конкурсов математических задач и головоломок (по-русски таких конкурсов в сегодняшней Сети, увы, нет). Эти конкурсы, как правило, обозначаются аббревиатурами POW или POM , где PO означает "problem of (the )"[1], а W / M означает периодичность появления новых задач на страничке конкурса — еженедельную ( week ) или ежемесячную ( month ).

Сводный список почти всех таких конкурсов содержится в каталоге Google (http://dir.google.com/Top/Science/Math/Recreations/Games_and_Puzzles/Problem_of_the_Week/). Здесь мы остановимся на некоторых наиболее крупных, популярных или примечательных с какой-то иной точки зрения.

Еженедельные конкурсы от Math Forum

http://mathforum.org/pow/ 

Здесь одновременно проводятся пять разных конкурсов — по алгебре, геометрии, элементарной математике, "пре-алгебре" (то есть по курсу, который предваряет стандартный курс алгебры), а также конкурс от колледжа Macalester, в котором новые задачи появляются каждую неделю, но решать их можно в течение всего учебного семестра.

Вот одно из последних конкурсных заданий по алгебре:

Рассмотрим класс таких последовательностей, в которых каждый член, начиная с третьего, равен сумме двух предыдущих[2] . Например: 2, 5, 7, 12, 19, ... где 7 = 2 + 5, 12 = 5 + 7, и так далее. Если первый член такой последовательности равен 1, а 10-й — 111, то чему равен второй член?

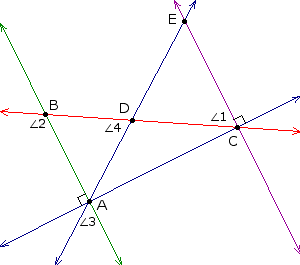
А вот свежая геометрическая задача:

Угол Ð 1 равен 2 x +10, угол Ð 2 равен 5 x -40, а угол Ð 4 равен 60 градусам. Найдите (в градусах) величины углов Ð 1, Ð 2 и Ð 3.

Еженедельный конкурс университета Пурдью (Индиана, США)

http://www.math.purdue.edu/pow/ 

Один из самых уважаемых конкурсов известного американского университета. Каждый семестр в конкурсе появляется 14 новых (действительно новых, а не переписанных из известных сборников) задач. Задания этого конкурса (как и некоторых других конкурсов в нашем списке) предназначены для американских студентов, поэтому вполне посильны для наших старших школьников.[3]

Текущая задача (последняя из октябрьских):

Существует ли множество, состоящее из более чем четырех точек пространства, такое, что любые четыре точки образуют тетраэдр единичного объема?

Замечу, что аналогичная задача для плоскости (в которой вместо тетраэдра рассматривается треугольник, а вместо четырех точек — три) давно и хорошо известна. В качестве ее решения годятся, например, 4 вершины квадрата.

Ежемесячный конкурс университета Бэйлор (Техас, США).

http://www.baylor.edu/math/index.php?id=21294 

В октябре предлагалась такая задача:

Найти все целые m и n, для которых 2^m = 3ⁿ + 5.

(Нетрудно увидеть, что годятся значения n=1 и n=3, при этом получаются m=3 и m=5 соответственно. Однако именно здесь в этой задаче и начинается интересная математика: существуют ли другие решения? Если да, то какие? Если нет, то почему?)

Ежемесячный конкурс университета Хемлайн

http://www.hamline.edu/~math/aguetter/pom/prob_of_month.html

По моим наблюдениям, авторы этого конкурса специально делают его с креном в сторону развлекательных задач и математических головоломок. Вот, например, первая из двух октябрьских задач:

Сузи, только что поступившую в университет Хемлайн, попросили помочь разобраться с урной, в которой находились 75 белых и 150 черных фишек. Сузи должна доставать фишки из корзины по две, и если хотя бы одна из двух взятых ею фишек черная, то ее она оставляет себе, но другая фишка немедленно должна быть возвращена обратно в корзину. Если же обе взятые фишки белые, то обе они остаются у Сузи, однако взамен она должна положить в корзину одну черную фишку (для этого у нее имеется необходимый запас черных фишек). Так Сузи поступает до тех пор, пока в корзине не останется только одна фишка. Какого цвета она будет?

Конкурс Эрика Фридмана

http://www.stetson.edu/~efriedma/mathmagic/ 

На сайте Фридмана "Магия математики" публикуются задачи, которые интересно решать независимо от возраста и уровня образования. Как правило, конкурсное задание состоит из нескольких задач, связанных общей тематикой. Обычно эти задачи хорошо исследуются при помощи компьютера, однако обойтись без напряжения мозгов при решении все равно не удается. Например, октябрьские задачи были посвящены повторяющимся блокам в квадратах натуральных чисел.

1. Число 16262² = 2644 5 2644  начинается и заканчивается на одни и те же 4 цифры. Фридман ставит задачу: отыскать наименьшее натуральное число, квадрат которого начинается и заканчивается на одни и те же N цифр.

2. Число 250125² = 625 625 15 625 содержит три "копии" трехзначного числа 625. Каким будет наименьший квадрат, содержащий C копий N-значного числа?

3. Какие квадраты содержат C*N цифр, при этом в разбиении их на C блоков по N цифр встречаются только два различных N-значных блока? Например, 727727² = 529 586 586 529 состоит только из трехзначных блоков 529 и 586.

Исследовательский конкурс от IBM

http://www.research.ibm.com/ponder/ 

Задачные конкурсы проводятся не только университетскими профессорами, но и некоторыми уважаемыми корпорациями. Говорят, что таким образом корпорации привлекли к себе на работу уже не один десяток светлых голов... Вообще говоря, я готов в это поверить: в конкурсе от IBM , как правило, помещаются весьма трудные "многоходовые" задачи. В общем, не зря он позиционируется как конкурс для лучших умов исследовательского отделения IBM. Впрочем, даже эти гробовитые задачи вполне традиционны. Например, в сентябре предлагалось усиление одной из задач, восходящих к колонке Мартина Гарднера из "Scientific American" 1979 года.

Двухнедельный конкурс от колледжа Wabash

http://persweb.wabash.edu/facstaff/axtellm/fortnight/fortnight.html 

Здесь, как правило, публикуются математические ребусы и другие головоломки, а победители конкурса посвящаются в "Рыцари Форта" ( FortKnight[4] ). Последний из конкурсных ребусов был таким:

В примере на умножение одна из цифр обозначена буквой X, а остальные остались неизвестными. Восстановите пример:

   ? XX ?
    ???
   ----
  ?? X ??
 ???? X
X ??? X
-------
???????

"Контест-центр" Фрэнка Рубина

http://www.contestcen.com/ 

Этот конкурс (точнее, группа конкурсов) — не только математический, в нем бывают задачи из самых разных областей знаний. Объединяет их то, что за официальное участие в конкурсе нужно заплатить определенную сумму, а большая часть собранных таким образом средств впоследствии распределяется между победителями конкурса. Этакое "Лотто-миллион", только роль случайности сведена к минимуму. Кстати, призовые суммы весьма и весьма немаленькие (в долларах — пятизначные), что свидетельствует о большой популярности конкурса. Впрочем, участвовать официально и платить вроде не обязательно: задания видны всем посетителям после (бесплатной) регистрации на сайте.

Шахматный ретроуголок

http://www.janko.at/Retros/ 

Я рискнул упомянуть шахматную страничку среди прочих развлечений, потому что здесь не требуется никаких специально шахматных познаний, достаточно помнить, как ходят шахматные фигуры. "Ретрозадачами" называется такая разновидность шахматных задач, в которых требуется не сделать несколько следующих ходов из данной позиции, а догадаться, какие именно ходы были сделаны последними. Сравнительно недавно появился еще такой подвид ретрозадач, как задачи на раскраску фигур. В них дополнительно требуется определить, какие фигуры в позиции — белые, а какие — черные. Помочь в этом может положение пешек, нахождение фигур под шахом и другие несложные наблюдения за позицией.

Вот свежее задание "ретроуголка":

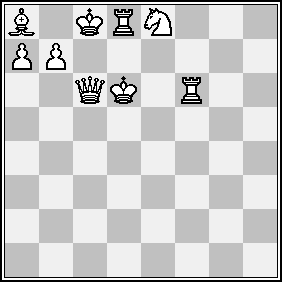
Требуется раскрасить фигуры и отыскать последний ход. (Решение этой задачи уже опубликовано и доступно на http://www.janko.at/Retros/Misc/Husserl1sol.htm)

Проект "Эйлер"

http://mathschallenge.net/index.php?section=project

Это — конкурс для любителей программировать задачи, имеющие математическое содержание. Как известно, Леонард Эйлер был не только великим математиком, но и прекрасным "вычислителем", неоднократно потрясавшим своих современников тем, с какой скоростью он мог производить в уме сложнейшие расчеты. Вот одна из типичных задач "проекта Эйлер":

Найдите единственную тройку натуральных чисел (a , b , c ), для которой a ²  +  b ²  =  c ² и a + b +c  =   1000.[5]

Программистские конкурсы

"Компьютерра" уже неоднократно писала (см., например, статью Дениса Коновальчика "Конкурс POTM и его братья", www.computerra.ru/offline/2001/402/10997/ ) об этой разновидности онлайн-соревнований, поэтому сейчас я ограничусь только упоминанием соответствующего каталога Google http://dir.google.com/Top/Computers/Programming/Contests/?il=1 и нескольких ссылок на русском языке, посвященных олимпиадам по информатике:

¨      Санкт-Петербургский сайт школьных олимпиад: http ://neerc . ifmo . ru /school /

¨      Московский сайт: "Олимпиадная информатика" — http:// www. olympiads. ru/

¨      Екатеринбургский сайт "Уральские олимпиады": http:// contest. ur. ru/

Настольные игры в вашем браузере

Вряд ли среди моих читателей найдется хоть кто-либо, кто ни разу не пытался играть против своего компьютера в шашки, шахматы, реверси ("Отелло"), крестики-нолики или  другие аналогичные настольные игры. Наверняка всем читателям известно и то, что современные программы умеют играть в такие игры весьма недурственно[6] . Понятно, что сражаться с такими программами-монстрами рядовому игроку неинтересно, а сознавать, что проигрываешь программе даже когда она играет на самом слабом уровне — еще и очень обидно. Что же делать? А вот что: играйте с примитивными программками, написанными на JavaScript и Java и разбросанными по всей сети. Выиграть у большинства из них очень легко, а если вы хотите просто узнать правила новой для себя игры и немного потренироваться, то ничего лучшего и не надо.

Шахматы. Рекомендую для начала http://www.browserchess.com. Как надоест — смотрите ссылки оттуда на другие сайты.

Шашки. Просто стоклеточные шашки. http://www.chez.com/jackbrc/essai10k.html

Нарды, они же — бэкгэммон. http://www.purebackgammon.com/

Го. В эту знаменитую игру в Сети можно играть и по е-мейл, и друг с другом, и против компьютера http://www.britgo.org/gopcres/play.html

Крестики-нолики http://ostermiller.org/calc/tictactoe.html

Скрэббл, также известный у нас как "Эрудит" и "Крестословица" http://www.isc.ro

Морской бой. http://www.battleships.f-active.com/

Реверси от Yahoo ! http://games.yahoo.com/games/login?game=reversi

Рэндзю, aka "Пять в ряд" http://renju.net.ru/

Монополия http://donotgo.com/seg/xlifeb.htm

Китайские шахматы — Xiang Qi — www.clubxiangqi.com

Китайские шашки, или "Солитер" (кажется, именно под таким названием у нас выпускалась игрушка, в которой надо было убрать с доски как можно больше фишек, перепрыгивая через них другими фишками, как в игре "Уголки".) http://www.tdbs.is.nl/scripts/interactief/game/Solitair/index_EN.asp Другая версия игры — http://www.justglass.com/flash/pegs.html

Быки и коровы, или Мастермайнд http://www.interjeux.net/jeux/mastermind/index_en.html

Манкала, или калах — одна из знаменитых настольных игр древности, наряду с го, шашками и нардами http://www.lookoutnow.com/game/man.htm

Менее известные игры:

Cosmic Encounter http://www.cosmicencounter.com

Mornington Crescent http://www.amazonsystems.co.uk/data/morn.htm

Quod http://wizard.ae.krakow.pl/~jb/Quod/

Ludo http://www.dohms.com/

Hnefatafl http://www.irt.org/games/js/hnefat/

Другие сайты, предоставляющие возможность поиграть одновременно в несколько различных игр, указаны в ссылках со страницы http://dir.google.com/Top/Games/Video_Games/Recreation/Browser_Based/Board_Games/Collections/

Иные околоматематические развлечения

Мир Эшера

http://www.worldofescher.com/

На этом сайте — воистину бесконечный мир живописи Мориса Эшера, в котором причудливые реальные объекты перемежаются с еще более причудливыми невозможными картинами и плавно перетекают один в другой, как рыбы и птицы на этом рисунке. В галерее вы найдете все наиболее известные работы Эшера — и руки, рисующие одна другую, и муравьев, ползущих по ленте Мёбиуса, и водопад, текущий снизу вверх, и многое другое... При чем здесь математика, спросите вы? Сходите на сайт — увидите сами...

"Математический Мир" и его соседи

(http:// mathwoorld. wolfram. com , http:// scienceworld. wolfram. com , а также http:// functions. wolfram. com , http:// integral. wolfram. com , http:// gallery. wolfram. com и другие сайты, см. список на http://www.wolfram.com/webresources.html)

Вольфрам в современном научном мире известен не только как химический элемент, но и как фамилия Стивена Вольфрама, одного из разработчиков программы Mathematica и автора замечательной книги "Наука нового типа"[7] . Ему же принадлежит и издательство, выпускающее литературу по современной математике. Именно поэтому под крылышком Вольфрама ныне обитает один из самых востребованных интернет-ресурсов, доступно и подробно рассказывающих о математике для непрофессионалов — математическая онлайн-энциклопедия http:// mathworld. wolfram. com . А сравнительно недавно там же открылись и смежные сайты. Например, integral — ресурс, позволяющий интегрировать функции, gallery — замечательная подборка "математических картинок"[8] , а functions — рассказ о свойствах различных математических функций (более 87000 разнообразных фактов — а ведь это почти столько же, сколько статей в Большой Советской Энциклопедии!).

WIMS

http://wims.unice.fr

Этот сайт называется " WWW Interactive Mathematics Server " и, надо сказать, полностью оправдывает свое громкое название. Вся интерактивная математика, которая только возможна, на нем есть. И даже больше... Тут есть и калькулятор для действий с матрицами, и переводчик из одной системы счисления в другую, и инструментарий для геометрических построений, и "сумматор", позволяющий считать конечные и бесконечные суммы.

Энциклопедия центров треугольника

http:// faculty. evansville. edu/ ck6/ encyclopedia/ ETC. html

Сколько различных центров может быть у треугольника? Вы думаете, что всего один? Ставлю вам двойку. Три? Четыре? Ладно, так и быть - тройка с минусом. Любители математики, наверное, смогут насчитать 7 или 8 точек, которые могут претендовать на звание того или иного центра треугольника. А вот Кларк Кимберлинг собрал в своей книге информацию про 400 таких точек, а на сайте перечислил и описал более 1100! K стати, при отыскании новых центров и их свойств очень активно используются современные математические пакеты. "Лежат ли такие-то три точки на одной прямой?" "Проходят ли такие-то три прямых через общую точку?" - на все эти и другие похожие вопросы можно получить ответ не вручную, а программно.

Энциклопедия целочисленных последовательностей

http://www.research.att.com/~njas/sequences/

Последовательности тоже удостоились отдельной энциклопедии (впрочем, книга, написанная автором этой энциклопедии - Нейлом Слоаном - впервые вышла еще до наступления PC -эры).

Обратный калькулятор

http://www.cecm.sfu.ca/projects/ISC/ISCmain.html

Вычислите на своем любимом калькуляторе что-нибудь типа log ( sqrt (2)* Pi ). А теперь впишите это число в строчку ввода на сайте "обратного калькулятора". Как вы думаете, что получится? А вот не поленитесь, поглядите сами. Или можете туда вписать что-нибудь не очень внятное типа 142857142857 - и тоже посмотреть на результат.

Математические константы

http://pauillac.inria.fr/algo/bsolve/

В каждой области математики есть свои постоянные величины. Точного и полного их списка не знает, вероятно, ни один из математиков. Однако к недостижимому идеалу вполне можно приблизиться. В общем, места знать надо...

Игра Монти Холла

http://montyhallgame.shawnolson.net/

Очень забавная java -игрушка, весь "сюжет" которой сводится вот к чему: имеются три картинки, на лицевой стороне которых находятся вопросительные знаки, а на обратной (невидимой для игрока) — смайлики, один веселый и два грустных. Игрок делает два хода. Первым ходом он указывает на любую из трех картинок, а в ответ одна из двух других картинок — та, на которой изображен грустный смайлик — переворачивается обратной стороной к игроку. То есть после первого хода игрок всегда видит одну открытую картинку с грустным смайликом. Вторым своим ходом он должен угадать, за какой из двух остальных картинок спрятан веселый смайлик. Казалось бы: картинок две, о них ничего не известно, значит, шансы 50/50. Как бы не так! Попробуйте поиграть в эту игру, всегда меняя ту картинку, на которую вы показали в первый раз. После нескольких игр сами убедитесь, что шансы на выигрыш — около 2/3. А если вы знаете теорию вероятностей, вам будет небезынтересно разобраться в том, почему так получается.

Словесные игры

Этот раздел не имеет прямого отношения к математике, однако, как я многократно убеждался, любители математики, познакомившись с описанными тут играми, неизменно признают их "своими".

"Данетки"

www. danetka. ru

Кажется, целая вечность прошла с тех пор, когда я публиковал в "Компьютерре" несколько подборок задач-данеток — замечательной игры, участникам которой предлагается коллективно разгадывать запутанные (а часто — криминально запутанные) ситуации, задавая ведущему вопросы, на которые тот может отвечать только "да", "нет" и "не имеет значения". Тогда мне приходилось напрягать всех своих друзей и знакомых в поисках новых интересных данеток, потому что по-русски никаких источников не существовало, а англоязычные сайты, как будто сговорившись, приводили одну и ту же подборку задач из книги " Lateral Thinking Puzzles "[9] ... Сравните: за полтора года существования сайта Данетка.Ру на нем задано отгаданы почти 900 данеток, для чего решателям потребовалось задать почти 50000 вопросов!

Другой сайт, на котором среди прочих задач можно найти и около сотни данеток по-русски — www. izvilina. com . Правда, новых задачек там практически нет, зато вся "классика жанра" — на месте, и притом (для лентяев) сразу с ответами.

А еще одно место, на котором иногда разгадывают данетки по-русски — ЖЖ-сообщество "Ру-Данетка", то есть www.livejournal.com/community/ru_danetka/

"Мафия"[10]

Описывать эту игру — дело утомительное, а также довольно скучное. При этом — совершенно неблагодарное: любителям "мафии" все скажет уже само название. В общем, всех остальных я прошу просто поверить, что эта игра захватывает похлеще квестов и паззлов... Поэтому отсылаю сразу к правилам: http://www.bratok.com/mafia/mafgame.shtml. Еще одно изложение для новичков — http://mafia-album.narod.ru. А вот здесь — собственно игра в онлайне и по е-мейлу: http://www.kozanostra.ru и http://www.mafiaclub.ru. На первом из них, кстати, предлагаются еще про две похожих коллективных игры — "Трын-трава"[11] и "Остракизм". Правила, ЧаВО, форумы, комментарии — в общем, все как полагается...