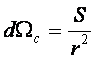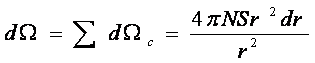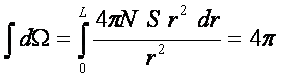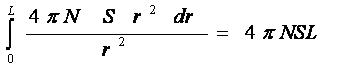Конкурс на решение задач по физике

Арбуз объявляет конкурс на решение задач по физике.

Приз - присвоение звание лучшего физика с выставлением фото (аватары) и биографии победителя на Арбузе.

Пятая задача - ответ до 15 марта.

С точки зрения энерго- потребления рассчитай- те основные физические параметры Матрицы - устройства, в котором тепловая энергия метаболизма и электро- магнитное излучение вследствие умственной деятельности людей используются в качестве источника энергии для машин, захвативших мир.

Четвертая задача - ответ до 8 марта.

Предположим, некая высокоразвитая цивилизация создала искусственную цилиндрическую "звезду" радиуса R и длины L>>R из вещества средней плотности D. Найти ускорение свободного падения на поверхности такой "звезды", а также вывести примерную форму третьего закона Кеплера для такого небесного тела.

Третья задача - ответ до марта.

Оцените время сдутия мыльного пузыря, сообщающегося с атмосферой через тонкую соломинку.
Физические параметры системы - на усмотрение решающего.
Автор: П.Л. Капица.

Вторая задача зимней серии:

Полый цилиндр заполнен жидкостью и покоится в пространстве (гравитацией пренебречь). Внутри цилиндра находится небольшой твёрдый шарик из вещества с плотностью, равной плотности окружающей жидкости.
Изначально, шарик покоится у "передней" стенки цилиндра. Неожиданно, цилиндр получает сильное ускорение в направлении от "задней" стенки к "передней" вдоль своей оси (скорости нерелятивистские) так, что шарик, очевидно, начинает двигаться в направлении "задней" стенки.
Достигнет ли шарик "задней" стенки?
Примечание - это не удар, а постоянно приложенное ускорение.

Авторы: Акакий Меликидзе, Илья Неменман (Принстон).

Решения шлите до 8 февраля на shurakbh[dog]mail.ru.

Первая задача зимней серии:

В строго вертикальный снегопад, лыжник движется вверх по горе и замечает, что в рот ему ежесекундно попадает N1 снежинок, а когда с той же скоростью вниз - N2 снежинок. Радиус снежинки R, скорость лыжника V, площадь его открытого рта - S. Оценить дальность прямой видимости в снегопад.

Примечание. Постоянная скорость падения снежинок равна U, эффективный радиус снежинки равен R << sqrt(S), а дальностью прямой видимости считать расстояние, с которого в среде практически не виден яркий точечный источник света. Снежинки считать совершенно непрозрачными, а плоскость разинутого рта лыжника - перпендикулярной земле.

Ура нашему первому участнику!

Решение задачи №1 январской серии о лыжнике-снегоглотателе прислано Владимиром Лутковским (vlut[пёс]list.ru) 21 января.

От Шуры:

Как многие уже догадались, занятная история про глотание снега – не что иное, как исходные данные для вычисления концентрации снежинок в воздухе. Вычисление это действительно очень простое, а посему оставим его на совести дорогих читателей Арбуза.

В случае уже известной концентрации, Владимир обрушил на эту задачу мощь своего интеллекта и всё моментально разъяснилось (кроме точечного источника света, который напрочь занавешен снегопадом). Ниже приводится решение Владимира, которому наша всеобщая  благодарность и поздравления:

Телесный угол, под которым видны диски непрозрачных снежинок, находящихся между r и r+dr, равен объему шарового слоя 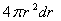, умноженному на число снежинок в единице объема N и на телесный угол, под которым видна каждая из снежинок (предполагаем, что все они одинаковы).Последний равен, очевидно,

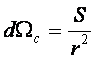
где S= πR²_c, где R_c - радиус снежинки. Итак, снежинки из шарового слоя занимают на небе телесный угол

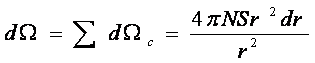
Найдем  расстояние L, такое, что при интегрировании по r от 0 до L получается телесный угол 4π, что и будет означать,  что снежинки в полученном шаре полностью перекрывают находящийся в r = 0 источник света. Это L и будет искомым расстоянием прямой видимости.

Итак,

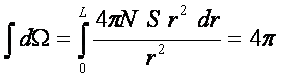
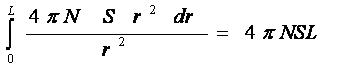
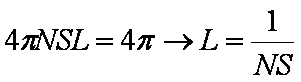
От Шуры:

Всё действительно просто и ясно, не правда ли? Следует отметить, что в данном случае, L – минимальная дальность прямой видимости, т.е. расстояние до источника света, когда каждая снежинка отбрасывает свою собственную тень (ни одна снежинка даже частично не находится в тени другой). Желающие могут развить эту тему и расписать распределение вероятностей попадания одних снежинок в тень других (областью попадания в тень отдельно взятой снежинки, очевидно, является усечённый конус) и найти соответствующие изменения в L, которое теперь  будет соответствовать среднестатистическому состоянию системы,  для чего  совсем необязательно отменять условие одинакового вектора скорости движения снежинок, т.к. речь просто идёт о наиболее вероятном положении снежинок друг относительно друга при перемещении наблюдателя вокруг источника света.  

Кстати, из решения Владимира  следует весьма интересный побочный результат: средняя площадь «тени» снежинки на расстоянии L >> R_c равна 3S и совершенно не зависит от значения L.

Слово нашему первому победителю.
...Действительно, это минимальная оценка дальности прямой видимости да еще в приближении строго геометрической (не волновой) оптики.
Краткое BIO: живу и работаю в архи-революционном Киеве, с младых ногтей обожаю решать задачки.Из "Кванта", олимпиадных сборников, Капицы и пр. Сейчас тружусь на тучной ниве экологического мат.моделирования. Хотя я уже вступил в пору зрелости, но это ребячество(щелкать хитроумные задачки) меня не покинуло. Мозги не должны простаивать и их очень полезно регулярно перенапрягать.

Материалы к размышлению(по В.Влад.Головачу(избранное):
Я не очень талантливый, но очень, очень умный.
Я очень люблю свою страну и не очень люблю свой народ.
Я точно знаю, что у меня есть чувство юмора, потому что я однажды нечаянно упал в нужник и вылез оттуда, смеясь.
Идеальная жизнь, как мне кажется, заключается в лежании на диване и чтении толстой книжки. Посколько у меня это не очень получается, приходится работать. Если уж работать, то хорошо.
Я считаю, что есть мало людей, которые что-то делают, и много людей, которые ничего не делают, а только треплются. Вторых не люблю.
У меня прекрасные друзья, но придурки.
Я еврей на четверть по крови и как минимум наполовину- по мироощущению.

Кстати, если угодно, есть одна замечательная задачка, к решению которой никак не могу подступиться: от чего больше зависит высота подъема брызг при падении камня в воду: от его скорости или массы? Как видите, постановка предельно проста.
Успехов.
В.Л.

Спасибо, Владимир! С победой!

Веду раздел я -- Шура, aka Смоляницкий Александр. В прошлом -- двукратный победитель республиканских олимпиад по физике для школьников в Узбекистане (1994, 1995), с 1995 г. учился на физфаке Самаркандского гос. университета (кафедра квантовой электроники) и даже заведовал сборной командой КВН университета.
С 2000 г. студент, а сейчас -- аспирант факультета Electrical Engineering в Illinois Institute of Technology, что на Чикагщине (http://www.ece.iit.edu) в области квантовых компьютеров.
Одновременно работаю в отделе разработок сверхточных измерительных приборов в Advanced Photon Source (http://www.aps.anl.gov), который является центральной частью Аргоннской национальной лаборатории (http://www.anl.gov).
Текущий проект, ежели кому интересно -- наноманипулятор для синхротрона, разрабатываемый для Центра по изучению наноматериалов.

Поскольку сайта своего не имею (времени нет, а ваять заранее мёртвого уродца нет смысла), но вот взамен некоторые ссылки, которые могут показаться интересными (кроме Арбуза):

http://star.tau.ac.il/QUIZ/  -- отличный конкурс на решение задач (на английском). Собственно, некоторые задачи, вывешенные на Арбузе, могут быть взяты с этого сайта.

http://www.jpl.nasa.gov -- сайт марсианских трактористов, т.е. Jet Propulsion Lab, где разрабатывались и разрабатываются многие интереснейшие проекты (в том числе, марсианские тракторы). Ужасно горжусь тем, что лично знаком с человеком, который там работает. :)

http://ocw.mit.edu/index.html -- совершенно шикарный проект в Массачуссетском технологическом институте (MIT). Тут можно выбрать совершенно бесплатный интернет-курс по весьма интересным дисциплинам.
Вот, например, курс по изучению энтропии для информационных систем. Учиться, товарищи, учиться и учиться!

И немного о самом конкурсе решения задач.
Кому нужен такой конкурс? Хотелось бы верить, что читателям Арбуза. Задачи, которые мы предлагаем, требуют твёрдых знаний не далее первого курса университета, но они нестандартны по своей сути, и требуют творческого подхода, а иногда -- недюжинных интеллектуальных усилий.
Некоторые читатели сразу поймут -- это классические "олимпиадные" задачи.
Далеко не все задачи будут иметь единственное и исчерпывающее решение,
и в таких случаях очень приветствуются ваши письма с рассуждениями, даже если более или менее формальное решение уже опубликовано.
Также, иногда могут публиковаться задачи совсем не по физике, а по электронике или теории информации и дизайну вычислительных систем.
На этом пока всё.
Удачи и до встречи на страницах Арбуза.