
|
|
|
|
|
|
|
|
|
Часы на весах или Куда смотрел Дж. УокерИсследование вечного арбузного вопроса о весе песочных часов прислал
Александр Смоляницкий, Illinois Institute of Technology (Chicago), shurakbh[dog]mail.ru. С вопросами и предложениями прошу в Форум. Предположим, имеются цилиндрические водяные часы, помещённые на пружинные весы (параметры весов мы обсудим далее), в которых вода движется квазистатически и ламинарно. Попытаемся проанализировать изменение веса идущих часов по времени.
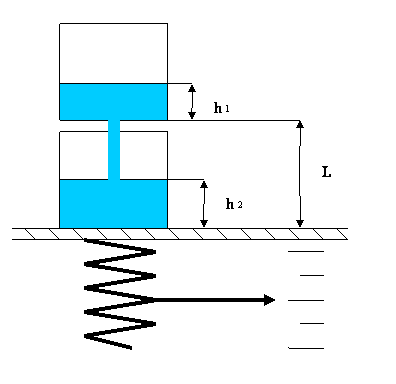
Рис. 1
Поскольку закон сохранения энергии в данном случае не соблюдается вследствие неэластичного взаимодействия между струйкой воды и сравнительно «неподвижной» водой в нижней камере часов (часть энергии внутри часов выделяется, в конечном счёте, в виде тепла, тогда как во взаимодействии часов как целого и пружины весов, энергия, конечно же, сохраняется), попробуем записать импульс системы в виде линейной комбинации импульсов воды в часах (относительно часов) и часов относительно земли, соответственно (направление движения «вниз» в данном случае принято за положительное):
P = M(dx/dt) + p
Где p х – линейное смещение (в единицах длины) весов от «нормального» веса часов с неподвижной водой, M – полная масса воды в весах Мы пренебрегаем импульсом медленно опускающейся воды в верхней камере часов и замечаем, что, несмотря на подъем центра тяжести воды в нижней камере часов, никаким вертикальным импульсом эта часть системы не обладает, а движение центра тяжести происходит вследствие квазистатического перераспределения потенциальной энергии воды. Массу самих часов будем читать пренебрежимо малой в сравнении с массой воды – предположение, в данном случае не вносящее ограничений на общую форму решения. Уравнение (1) есть ни что иное, как выражение закона сохранения импульса – вода, покидающая верхнюю камеру часов и неэластично ударяющая в нижнюю камеру, неизбежно влияет на общее движение часов на весах. К тому же, в любой момент времени (во время квазистатического процесса), небольшая часть воды практически свободно падает, уменьшая общую силу взаимодействия часов с весами – эта часть решения будет добавлена далее. Попробуем найти явную зависимость p
dp
где D – плотность воды, а – поперечное сечение струйки воды (определяемое поперечным сечением отверстия в верхней камере часов – мы пренебрегли сужением струйки вследствие поверхностных эффектов. В случае непрерывающейся струйки, в общем случае, можно ввести эффективную площадь поперечного сечения струйки воды), v(y) – скорость движения воды в струйке в зависимости от высоты y ( y v(y)становится:
v(y) = (2g (h
p В общем случае, полное выражение для (1.2) для произвольного L > h
p
где мы использовали кажущееся очевидным выражение:
dh
** Интересно заметить, что более точное выражение, (вывод которого предлагается читателю в качестве упражнения) даётся в виде dh Запишем первую производную (1) по времени:
dP/dt = dp
где, с использованием (1.3) имеем:
dP/dt = M(d
Таким образом, выражение 2-го закона Ньютона выглядит следующим образом:
M(d
где k и β’ – обещанные параметры самих весов – жёсткость пружины и коэффициент затухания в данном случае, соответственно. Поделив на общую массу часов, получаем неоднородное уравнение затухающих колебаний:
x” + βx’ + ω
где (1/M)dp
β = β’/M; ω Очевидно, что решением (5) будет являться сумма «обычных показаний весов» (решение однородного уравнения и добавочного сдвига вследствие силы тяжести) и изменения вследствие процесса перетекания воды. Чтобы определить параметр в правой части (5), а также определить период водяных часов, рассмотрим процесс перетекания воды (мы снова используем соотношение Бернулли для скорости воды, покидающей верхнюю камеру часов):
Прямое интегрирование даёт функцию изменения h
h где h Очевидно, что h
h
а полное время перетекания воды
T = α
Непосредственно из (7), уравнение (5), таким образом, может быть полностью определено, однако ввиду формы решения (6) становится весьма неудобоваримым для решения. Для получения приблизительного описания поведения системы, мы поступим иначе, разложив (1.3) в ряд Тейлора до члена третьего порядка (чтобы определить производную импульса до второго порядка) и только результат разложения (с учетом (6) ) подставим в (5):
p - (1/4) α
Как видно из предыдущего уравнения, эффект более высоких порядков уменьшается пропорционально α
Таким образом, из (8)
dp
Отсюда, (5) можно выразить в виде:
x” + βx’ + ω
или
x” + βx’ + ω
Отметим, что (10) определяет вес часов только вследствие переноса импульса и не принимает во внимание уменьшение веса вследствие свободно падающей части воды (будет добавлено далее). Решением (10) будет являться, очевидно, сумма однородного варианта (10) (затухающие колебания), «сдвига» вследствие силы тяжести (определяющего, собственно говоря, «вес», показываемый весами) и, наконец, изменение веса вследствие работающего «реактивного двигателя» внутри часов. Немного упростив (10) и для простоты убрав из (10) дампер β, мы имеем для относительного изменения среднего веса в силу переноса импульса:
ΔW
Изменение среднего веса в силу «падающей» воды, используя (6) и принимая во внимание L ~ h
ΔW что ровно на порядок 1/α «сильнее» предыдущего!
Хотя выражения (11) и (12) не являются независимыми друг от друга, всё вышеприведённое является следствием применения теории возмущения и может быть применено для квазистатического процесса в качестве оценки. Попробуем рассчитать процентное отклонение от среднего веса для водяных часов с периодом в 60 секунд, общей массой воды в 100 грамм и радиусом цилиндра часов в 3 см:
h
Относительные изменения веса в процентах (Matlab):
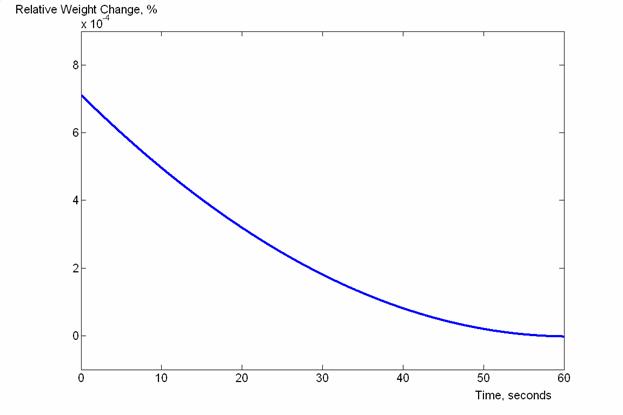
Рис. 2 – Изменение веса вследствие только переноса импульса.
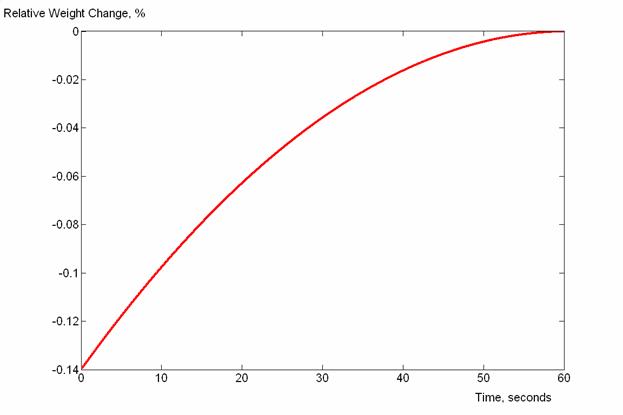
Рис. 3 – Изменение веса вследствие только «невесомой воды»
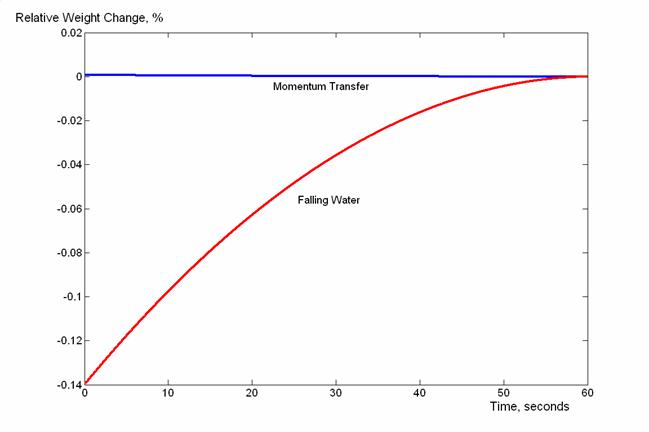
Рис. 4 – Сравнительное изменение веса вследствие двух процессов в отдельности
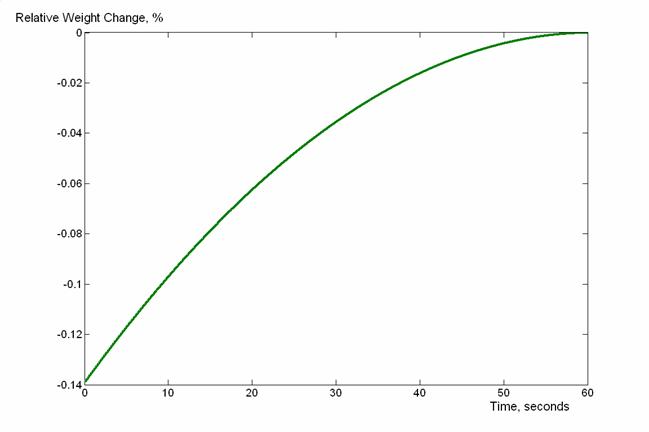
Рис. 5 – Изменение веса вследствие двух эффектов в совокупности
Как видно из графиков, увеличение веса вследствие переноса импульса, обещанное Дж. Уокером, ни в коей мере не компенсирует потерю веса вследствие того, что часть воды в часах пребывает в невесомости. В то же время, экспериментальное обнаружение эффекта возможно только в случае точности весов, превышающей десятые доли грамма. Эффект затухания также очень важен: с учётом β, решение (5) выглядит отлично от полученных результатов – весы попросту «не успевают» за изменением веса системы. Также, приближение L
Почему неправ Дж. Уокер? Или так: где я потерял один порядок величины (под порядком величины, в данном случае следует считать степень α)? Забудем на минуту о водяных часах и заменим её простым вертикальным штативом массы М, на котором, на высоте h, находится грузик массы m (m<<M). Изменение веса вследствие падающего грузика равняется, очевидно mg, а относительное – (m/M) – назовём его ради прикола α! Упавший грузик изменит вес системы на весах (математическая выкладка очень проста) на среднее относительное значение в α Только если kh в 1/α больше веса часов, мы можем говорить о какой-то взаимной компенсации двух эффектов, а сам эффект присутствия квадрата массового соотношения появляется элементарно в силу потери энергии внутри часов (импульс грузика уже при соударении умножается на дополнительное α, как следствие неэластичного соударения!) .
Для примера компенсации, возьмём штатив массой в 100 г, массой грузика в 1 г, при жёсткости пружины весов 100 Н/м (смещение при весе в 1 кг -- примерно 1 см) и высоте штатива в 10 см, относительные изменения веса в силу каждого из эффектов равны между собой (0.01), то есть, увеличение L (см. выше) действительно может не только взаимно компенсировать оба эффекта, но и возможно сделать часы на весах тяжелее (не следует, однако, забывать, что с увеличением L также линейно возрастёт и количество падающей воды). В рассмотрении водяных часов, мы преспокойно выбрали наше значение h близким к массовому параметру «штатива» (L
Пример со штативом, собственно, уже подводит нас к задаче о песочных часах. Несмотря на то, что система с песочными часами дискретна в отличии от водяных часов, принципиальная разница состоит лишь в том, что песок покидает верхнюю камеру часов со скоростью много меньше (2g h
Конус, образуемый песчинками в нижней камере часов, также можно определить математически. Легко показать, что тангенс угла при основании центрального продольного сечения конуса (очень хотелось бы, чтобы равнобедренного треугольника) примерно будет равняться коэффициенту трения между поверхностями песчинок. Для простоты, его можно принять за единицу (песок – штука шершавая!), и мы будем иметь конус с высотой, равной радиусу его основания. Используя формулу объема, можно очень просто рассчитать параметры роста конуса в зависимости от потока песчинок и, тем самым, математически описать внутреннюю динамику системы.
p.s. А что же само время? Даже без СТО, что-то подсказывает, что не будут такие скачущие на весах часы шибко точными. J
(с) A.S. 12.2004 |
| Автор | )c( 2000-2019 Kопирайта нет, копируйте на здоровье :) 100112 лет в Интернете |
|
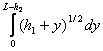 (1.2)
(1.2)