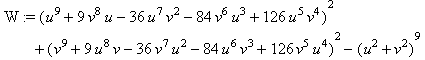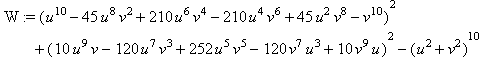Пифагоровы тройки, как частное решение

            Пифагоровы тройки – это натуральные числа, образующие группу прямоугольных треугольников. По открытой еще древними математиками истине, данные числа удовлетворяют диофантову уравнению 

                                         x² + y² = z²                                                 ( 1 )

Таковы, например:  x = 3 ,  y = 4 ,  z = 5    или  x = 5 ,  y = 12 ,  z = 13 . Все тройки взаимно простых  Пифагоровых чисел можно получить из аналитических формул:

          x = u² – v²  ,      y = 2uv   ,      z = u² + v² ,                       ( 2 )

где  u   и  v  принадлежат натуральному ряду,  u > v > 0 .

            Если   u   и  v   взаимно простые, то сумма их квадратов образует особую группу целых положительных чисел  z .  Например,  2² + 1² = 5 ,   3² + 1² = 10 ,   3² + 2² = 13  и так далее. Предположительная особенность такова. Если   n = 1,  2,  3, …, то диофантово уравнение

                                        x² + y² = zⁿ                                                 ( 3 )

однозначно существует только при упомянутых выше значениях  z .  Если это действительно так, то Пифагоровы тройки  являются частными решениями соотношения (3). Из сказанного следует, что скорее всего нет ни одного целочисленного тождества для      x² + y² = 6ⁿ  ,  но зато существует хотя бы один набор   x , y , n   при котором реализуется уравнение    

x² + y² = 5ⁿ   Например: 

                                               7² + 24² = 5⁴  ;     

                                  2642² + 6469² = 5¹¹  .    

            Мои доводы – это всего лишь гипотеза. Доказать ее, по всей видимости, не легче, чем Великую Теорему Ферма, но численными примерами можно удостовериться в правильности рассуждений хотя бы для нескольких тысяч вариантов.

            Чтобы решить проблему эффективно, необходимо выполнить компьютерные расчёты. Автор решил вычисления проделать в редакторе Maple10.  Это один из самых мощных математических продуктов современности, позволяющий производить анализ как в символьном, так и в калькуляторном режиме.

            Программирование в упомянутой среде настолько упрощено, что можно обойтись буквально пятью строками команд. Вот они:

u:=2:v:=1:k:=2:m:=2:z:=u^2+v^2: t:=100000:for n from 1 to 6 do print(n); for y from 1 to t do if z^n>y^m then x:=simplify((z^n-y^m)^(1/k));x1:=trunc(x);if x=x1 then  print(x,y,z,ifactor(x),ifactor(y)) fi;fi; od od;

Сначала задаются два взаимно простые числа  u  и  v  ,  причём в данном случае неважно, какое из них больше. Показатели степени  k  и  m  приняты равными двум. После вычисляется  параметр  z .  Далее идут два встроенных цикла. Внешний цикл изменяет показатель степени  n  от 1 до 6, а на внутреннем цикле производится выборка решений. Поясним некоторые команды:   simplify    - упрощение выражения ;  trunc     -  выделение целой части десятичной дроби;  ifactor    -    разложение целого числа на простые множители. По этой программе получаем серию вариантов для одного значения  z:

Выпишем допустимые соответствия:

  1² + 2² = 5¹  ;          3² + 4² = 5²  ;             2² + 11² = 5³   ;      

  7² + 24² = 5⁴    ;   38² + 41² = 5⁵  ;         44² + 117² = 5⁶

Подчеркнутый вариант – это первая Пифагорова тройка. Наверное, достаточно лишь понять законы изменения последовательностей чисел  x  и  y , чтобы найти общий метод поиска остальных троек чисел. Приведем еще несколько результатов:

 1² + 3² = 10¹  ;            6² + 8² = 10²   ;       18² + 26² = 10³

28² + 96² = 10⁴  ;    12² + 316² = 10⁵   ;   352² + 936² = 10⁶

В этой серии четных чисел лишь члены Пифагоровой тройки (они не взаимно простые) можно поделить на 2² , превратив этот вариант в  3² + 4² = 5². Во всех остальных равенствах такой фокус не получится.

Очередная порция тождеств:

2² + 3² = 13¹  ;               5² + 12² = 13²   ;           9² + 46² = 13³

119² + 120² = 13⁴    ; 122² + 597² = 13⁵  ;     828² + 2035² = 13⁶

И так далее…

Если бы хоть один житель Земли знал, чего мне стоило найти строгие алгебраические связи! Но муки творчества позади  и теперь можно дать общий метод.

Выражение  (3)  перепишем  в виде:

x² + y² = (u² + v²)ⁿ   ,                      ( 4 )

где  значения  u   и  v   - такие же, как и в (2).

            Cначала построим своеобразную Таблицу Паскаля, позволяющую не только получать биноминальные коэффициенты, но и определять знаки перед ними:

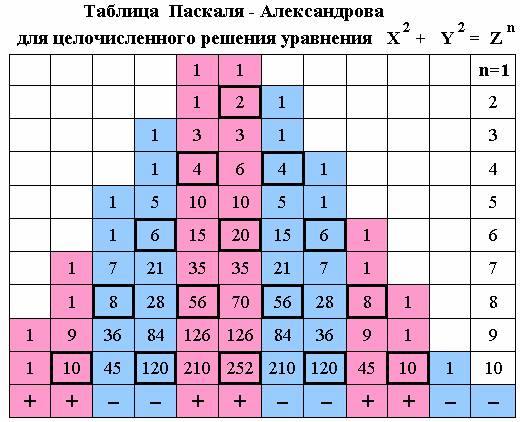
Конечно же, я нашел теоретические формулы для составления готового тождества при любом значении n , но они настолько громоздкие и непривлекательные, что лучше рассмотреть конкретные примеры с описанием общих правил конструирования алгебраических соотношений.

1 . Если показатель степени  n  - число нечетное, то достаточно получить выражение только для   x , а  уж  y  формируется путем формальной  замены  u  на  v   и  v  на   u .

                Итак, пусть  n = 7.   Находим по таблице нужную строку. Биноминальные коэффициенты:  1 , - 7 ,  - 21 ,  35 ,  35 , -  21 ,  - 7 ,  1 .  Знаки перед числами зависят от цвета поля, где они находятся. Если цвет малиновый, то ставится плюс, если же голубой, то минус. Для формирования  x и  y  потребуется лишь половина этих цифр:

                       x = | u⁷ – 7 v⁶ u – 21 u⁵ v²  + 35 v⁴ u³ |           ( 5 )  

Если отказаться от модуля, то может получиться отрицательное значение  x , что тоже, однако, является решением. Здесь многочлен всегда начинается с  un . Затем во втором слагаемом появляется  vn-1  , в третьем  un-2  и так далее. Начиная со второго члена приписывается сомножитель-дополнение. Сумма их показателей степени всегда равна  n

( например, 6 + 1 = 7,   5 + 2 = 7  и так далее).

 Параметр  y по структуре такой же, как  (5) :

                     y = | v⁷ – 7 u⁶ v – 21 v⁵ u²  + 35 u⁴ v³ |           ( 6 )

                Проверим в  Maple10,   будет ли   x² + y2  =  ( u² + v²)⁷ :

 W:=x^2+y^2-(u^2+v^2)^7;

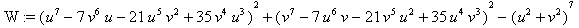
 W:= factor( W );

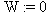
            В самом деле, получено алгебраическое тождество, справедливое для действительных  (а не только целых)  чисел.

                Еще пример. Примем  n = 9.  Тогда сразу пишем:

x = | u⁹ + 9 v⁸ u – 36 u⁷ v²  – 84 v⁶ u³ + 126 u⁵ v⁴ |

y = | v⁹ + 9 u⁸ v – 36 v⁷ u²  – 84 u⁶ v³ + 126 v⁵ u⁴ |

Проверяем тождество (4):

 W:=x^2+y^2-(u^2+v^2)^9;

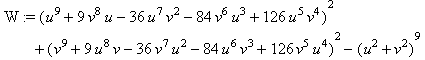
 W:= factor( W );

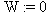
                Теперь уже можно стопроцентно гарантировать безупречность методики при нечетных   n .

                2 .  Если показатель  n  четный, то технология несколько иная. Здесь уже будут задействованы все биноминальные коэффициенты.  Те из них, которые не выделены жирной рамкой, потребуются для формирования  x , а  выделенные – для   y .

                Пусть  n = 6 ,   Конструируем  выражение  x.  Рассматриваем только коэффициенты, не выделенные рамкой.  Первый член, как и в предыдущих примерах, - это  un  со знаком минус (согласно таблице).  Второе слагаемое  –  это  + 15 un-2 v2  .  Третье слагаемое:

 – 15 un-4 v4 .     Если бы число n было больше шести, то процесс продолжался бы, каждый раз изменяя показатели степени на двойку. Последний член – это  + vn . Применим  рекомендации к рассматриваемому случаю:

                  x = | – u⁶ + 15 u⁴ v² – 15 u² v⁴ + v⁶ |

Для формирования  y  используем только цифры в рамках. Здесь показатели степени обязательно нечетные  и снижаются для параметра  u :

                  y = | – 6 u⁵ v  + 20 u³v³ – 6 u v⁵ |

Проверим правильность построений:

W:=x^2+y^2-(u^2+v^2)^6;

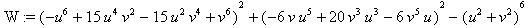
 W:= factor( W );

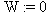
Формула работает. Проверим еще для  n = 10 :

x = | u¹⁰ – 45 u⁸ v² + 210 u⁶ v⁴ – 210 u⁴ v⁶ + 45 u² v⁸ – v¹⁰ |

y = | 10 u⁹ v – 120 u⁷ v³ + 252 u⁵ v⁵ – 120 u³ v⁷ + 10 u v⁹  |

 W:=x^2+y^2-(u^2+v^2)^10;

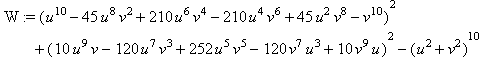
 W:= factor( W );

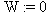
                Итак, метод доказан для довольно сложных вариантов. Теперь, исходя из данной модели, легко найти  выражения для генерации Пифагоровых чисел.

                Имеем случай  n = 2.  При помощи таблицы тут же выявляем:

                               x = | u² – v² | ;          y =  | 2 u v |  .

                Получены числа Пифагора, которые находятся из частного решения уравнения  ( 4 ).

Новые афоризмы:

Будь Пифагор с нами,  он бы женился на компьютере. Числа уводят так далеко, что забываешь число, месяц и год. Найти решение -  значит, прорвать оборону тайны.   Палиндромы: Зуб  Раи  -  арбуз ! Воз убран арбузов. Арбуз у зубра.   Георгий Александров Специально для www.arbuz.uz Май 2006 г. Москва

 

20 апреля 2006 г     Специально для www.arbuz.uz