Магические квадраты порядка одинарной чётности

            Одинарная чётность описывается простым целочисленным уравнением:

n = 4 k + 2,       где k = 1 , 2 , 3 , …

Построение магических квадратов именно этого порядка оказалось наиболее трудным, нежели МК других видов (см. мою статью на странице  www.arbuz.uz/s_mk ). Сказанное объясняется тем, что чётно-нечетный рисунок матрицы размером  (4k + 2)  х  (4k + 2) не получается симметричным.

Но можно ли найти способ составления данного МК, понятный любому здравомыслящему человеку? Такую задачу мне удалось решить буквально на днях.

Подробно опишем  последовательность действий для n = 14 ,  то есть   k = 3.

1.  Закрашиваем желтым цветом главные диагонали. По углам расставляем цветные квадратики строго определенным образом:

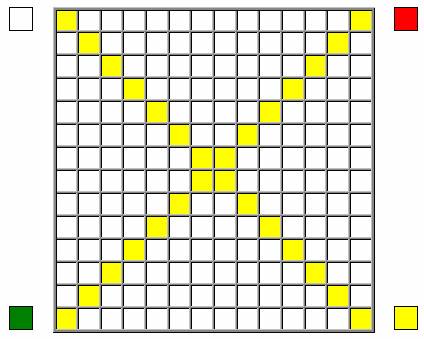
2. Утолщаем верхнюю часть диагоналей в k  раз:

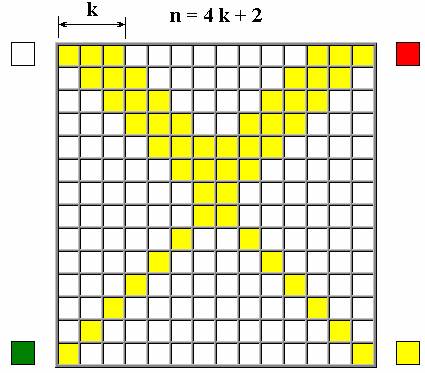
3. То же самое делаем с нижней частью диагоналей.

4. Добавляем с двух боков ступенчатые трапеции высотой  k – 1:

5. Левую трапецию полностью окружаем зелеными ячейками:

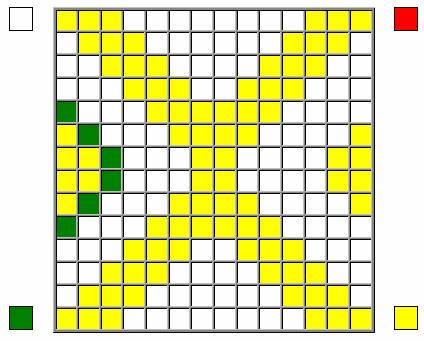
6.      В верхней и нижней чашах добавляем зелёные ветви:

7.  В верхней чаше красными ячейками ограничиваем трапецию, конгруэнтную жёлтой:

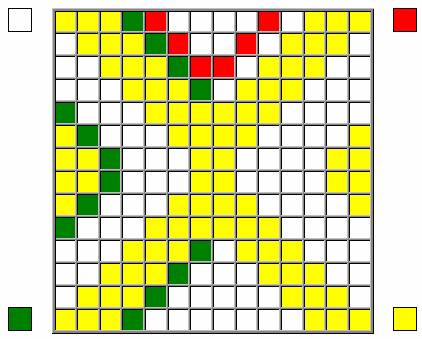
8. Симметрично устанавливаем красные ветви:

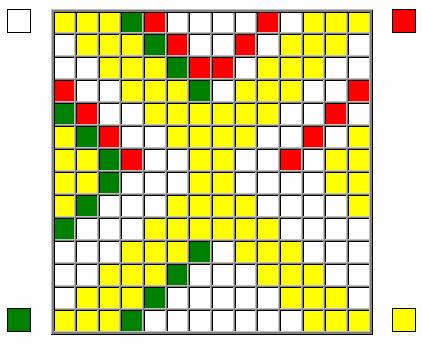
Матрица для построения МК готова. Осталось регулярным способом пронумеровать ячейки со всех четырёх сторон (нумерация ведется горизонтально и послойно):

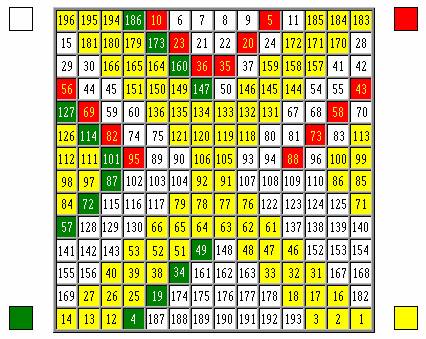
Проверим данную матрицу на магичность при помощи электронной таблицы Excel:

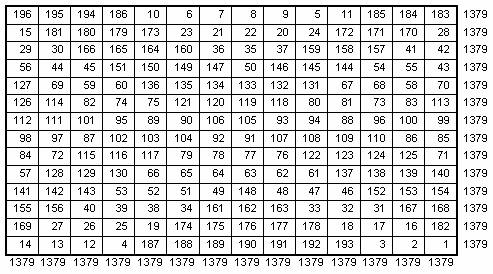
Главные диагонали также дают магическую сумму  1379.

Так просто и наглядно строится любой МК порядка  6 , 10 ,  14 ,  18 ,  22 ,  26 , ….

Я объяснил методику соседу по квартире (ему 13 лет). Он всё прекрасно понял и за три часа сумел самостоятельно построить МК порядка  38. Причем без применения каких-либо счетных устройств. Проверка внушительной матрицы в Excel показала, что везде присутствует магическая сумма  27455. Всего ему пришлось написать 1444 числа.

            Только пройдя трудный путь можно найти легкий метод.

Георгий Александров , 13.06.2006,  Москва.

Специально для  www.arbuz/uz