БЛОГ • Форум • Ссылки • Написать письмо • Почему Арбуз? • Служебная • UN • ЕЖЕ-движение - международный союз интернет-деятелей

Магические квадраты и палиндромы от Георгия Александрова

 

Уважаемый Евгений!
 Посылаю Вам метод построения магического квадрата нечетного порядка, который я сам разработал. Широко известны способы Баше, Лубера и других. Но моё решение, пожалуй, самое простое. Это хорошо видно из прилагаемых иллюстраций. Сперва выделяется ромбовидное ядро (желтый цвет), который заполняется регулярным способом нечетным рядом чисел. Затем методом отражения выделяется более округлое ядро путем отражения ступенчатого треугольника относительно двух сторон рамки. Это ядро также регулярно заполняется четным рядом чисел. Далее осуществляется простой перенос треугольных элементов по горизонтали, вертикали и диагонали. У меня даже дух захватило, когда получил такое!
Даже сомнение возникло: может, не я первооткрыватель? Но как ни старался найти в литературе нечто похожее, - ничего не обнаружил.
Если читателям "Арбуза" удастся найти первоисточник, то умоляю сообщить на renuar911[dog]yandex.ru
С уважением, Георгий Александров.

 

Метод построения магического квадрата нечетного порядка.

Метод разработал Георгий Александров

 

 

Магический квадрат порядка двойной чётности.





 

 

Магический квадрат порядка одинарной чётности.

 

Порядок одинарной четности  n = 4 k + 2  , где  k = 1,  2,  3,  …  Минимальное значение  n   в данной группе равно  6 . Квадратную матрицу  6 х 6  оформим следующим образом:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

В итоге мы имеем укрупненную матрицу нечетного порядка,  каждая  ячейка которой – квадратный элемент  размером 2 х 2 .   Если теперь в каждый элемент 2 х 2 включать все цифры от 1  до  4 , то достаточно легко найти такие расстановки чисел, что получается упрощенный магический квадрат  6 х 6.  Приведем несколько таких примеров:

4

1

2

3

4

1

2

3

1

4

2

3

4

2

2

1

4

2

1

3

4

3

1

3

1

4

2

3

1

4

3

2

4

1

3

2

 

1

2

1

4

3

4

3

4

3

2

1

2

4

2

1

2

4

2

3

1

3

4

3

1

1

2

3

2

3

4

3

4

4

1

1

2

 

4

1

3

2

4

1

3

2

1

4

3

2

1

3

3

4

3

1

4

2

1

2

2

4

1

4

3

2

1

4

2

3

4

1

2

3

Магическая сумма во всех упрощенных квадратах равна   2,5 n , то есть в наших случаях  15

С целью большей наглядности последнее решение лучше представить графически:

 

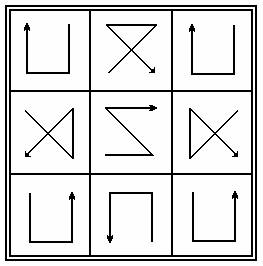
Для того, чтобы построить следующий упрощенный магический квадрат,  то есть порядка   n =10 ,  достаточно по периметру добавить пояс условных  значков:

 

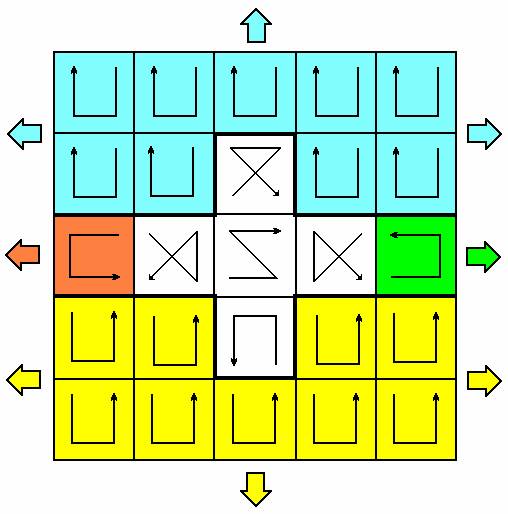
Выделенный горизонтальный коридор, а также две обширные закрашенные области, неограниченно простираются  в стороны, позволяя  тем самым создавать более крупные матрицы порядка  4k +2.   Каждая цветная стрелка подсказывает, что в данном направлении никакие другие значки включать не нужно.

Итак, мы свели задачу к построению магического квадрата нечетного порядка n / 2,  в котором каждая ячейка  2 х 2  имеет выявленную только что последовательность расстановки чисел.

Так же, как и в случае магического квадрата нечетного порядка, выделяем два ядра: чётное и нечётное, сохранив  при переносе ячеек условные значки. Далее записываем простой натуральный ряд чисел, последовательно переходя от нечетного ядра к чётному и обратно. На следующем рисунке показана начальная стадия заполнения ячеек.

 

 

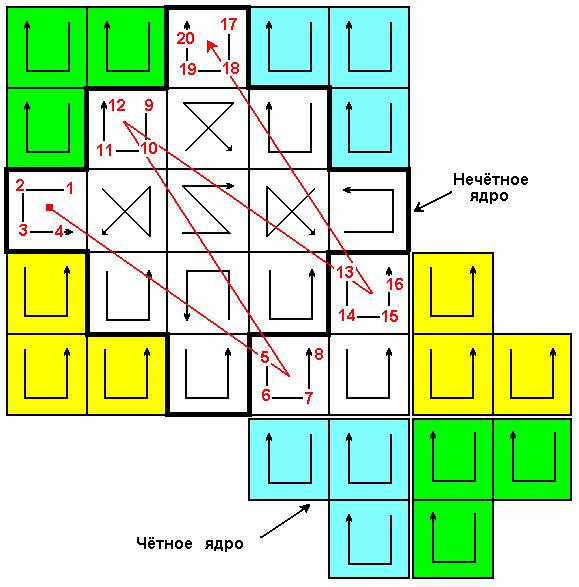
Если все числа грамотно расставить, то получим следующее:

 

 

 

 

 

 

20

17

 

 

 

 

 

 

 

 

 

 

 

 

19

18

 

 

 

 

 

 

 

 

 

 

12

9

35

34

60

57

 

 

 

 

 

 

 

 

11

10

33

36

59

58

 

 

 

 

 

 

2

1

25

27

51

52

75

73

100

99

 

 

 

 

3

4

28

26

49

50

74

76

97

98

 

 

 

 

 

 

41

44

67

66

89

92

13

16

37

40

 

 

 

 

42

43

68

65

90

91

14

15

38

39

 

 

 

 

 

 

81

84

5

8

29

32

53

56

77

80

 

 

 

 

82

83

6

7

30

31

54

55

78

79

 

 

 

 

 

 

24

21

48

45

72

69

96

93

 

 

 

 

 

 

23

22

47

46

71

70

95

94

 

 

 

 

 

 

 

 

64

61

88

85

 

 

 

 

 

 

 

 

 

 

63

62

87

86

 

 

 

 

Теперь возвращаем цветные треугольные элементы с цифрами на свои места внутри квадрата:

 

 

72

69

96

93

20

17

24

21

48

45

71

70

95

94

19

18

23

22

47

46

88

85

12

9

35

34

60

57

64

61

87

86

11

10

33

36

59

58

63

62

2

1

25

27

51

52

75

73

100

99

3

4

28

26

49

50

74

76

97

98

37

40

41

44

67

66

89

92

13

16

38

39

42

43

68

65

90

91

14

15

53

56

77

80

81

84

5

8

29

32

54

55

78

79

82

83

6

7

30

31

 

 

Это действительно магический квадрат десятого порядка 

Если отталкиваться от построения МК порядка двойной чётности, то можно получить регулярный метод. Шаблон для n = 10   имеет вид:

 

 

 

à

 

 

 

 

 

 

–

 

 

 

ß

 

 

 

 

 

 

 

 

–

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

–

 

 

 

 

 

–

 

 

 

 

 

 

–

–

 

 

 

 

–

 

 

 

 

 

 

 

 

–

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

–

 

 

 

 

 

 

 

à

 

 

 

 

–

–

–

 

 

 

ß

 

 

Точкой помечены незыблемые ячейки по отношению к осям симметрии МК. Далее красно-синие плитки чередуются в шахматном порядке вплоть до желтого центрального квадрата 2 х 2 .

 

Заполнение производится в четыре стадии:

 

 

à

1

2

98

4

96

95

97

93

9

10

ß

 

 

 

11

89

13

87

15

86

84

18

82

20

 

 

 

 

80

22

78

24

76

25

27

73

29

71

 

 

 

 

31

69

33

67

35

66

64

38

62

40

 

 

 

 

60

42

58

44

56

55

47

53

49

41

 

 

 

 

50

59

43

57

46

45

54

48

52

51

 

 

 

 

70

39

63

37

65

36

34

68

32

61

 

 

 

 

30

72

28

74

26

75

77

23

79

21

 

 

 

 

81

19

83

17

85

16

14

88

12

90

 

 

4

à

91

92

8

94

5

6

7

3

99

100

ß

 

 

 У автора в комнате висит грандиозное чудо математики – магический квадрат 102  × 102 , который был заполнен именно по этой методике.

С уважением,

                                  

 

 

25 января  2006 г.

 

 

Палиндромы от Георгия Александрова


 

Лиры Толя вяло тырил

Ушаков ел клево кашу

Иру, Дима, сам и дури!

Да, Гена - не гад!

Гене давал Слава денег

Саша - наш ас!

Я + Наташа = Саша + Таня

Жил около Коли ж

Не видно Коли. Локон дивен!

Асе - беса!

Ел ли Ваня на вилле?

Сева!  - вес!

Алиса басила

И, луну дивя, в яви дунули

Мил? - Оголим!

От Раи - пиар-то!

А Калинину - ни-ни лака!

На море, Тихомиров, творим о хите роман

А в Тибете - битва


 

Еще на Арбузе палиндромы смотрите тут

 

 

Автор about me
Design by dady_MYKC
 		)c( 2000-2019
Kопирайта нет, копируйте на здоровье :)

100112 лет в Интернете


.