Волнолом из блоков

      Прежде чем приступить к рассмотрению другой задачи, позволю себе небольшое отступление.

Просматривая научные форумы, я натолкнулся на довольно нелестные высказывания по поводу публикуемых мной материалов. Одним кажется, что задачи и решения находятся на уровне понимания детей, другие считают, будто поднимаемые вопросы стыдно помещать на страницах «Арбуза». Обидно, что об этом говорят люди, сами ничего особенного не создавшие. Им, наверное, неведомо, каким каторжным трудом добываются даже малые крупицы истины. Особенно в такой дисциплине, как теория чисел. Вопреки таким высказываниям, ко мне на электронную почту приходят письма из России, ближнего зарубежья и даже из Японии с просьбой  пояснить отдельные моменты и просто со словами благодарности. А только вчера из университета Джакарты я получил целое послание от одного аспиранта со словами благодарности, поскольку один из моих описанных методов помог в решении конкретной задачи.

 То, о чем я буду сейчас говорить, выстрадано тридцатилетней борьбой с другими невеждами, считавшими, что простейшие кладки (придуманный мною математический термин) невозможно оптимизировать. Когда же красивые решения были получены, опубликованы монографии, защищены диссертации и прошли выступления на международных конференциях,  оппонентам ничего не оставалось делать, как принести мне свои извинения.

            Теория простейших кладок очень сложная, но ее прикладную практическую суть удалось упростить настолько, что теперь кажется непонятным, почему идея не пришла в головы ни математикам, ни инженерам на протяжении почти четверти тысячелетия (впервые конструкция мола из бетонных блоков массой 100 тонн была построена  французским инженером Беллом еще в 1861 году).

            Итак, применим Комбинаторную Матрицу Сложения к проектированию секции волнолома из блоков-параллелепипедов.

            Будем решать задачу в рамках следующих требований:

            1. Число типов блоков равно двум.

            2. Число типо - размеров блоков в плане равно трём.

Это означает, что элементы имеют одинаковые не только высоты, но еще один габарит. Например,   5 x 4    и    5 x 3   или же    7 x 5   и   6 x 5   и так далее. Следить нужно лишь за двумя вещами: 1) минимальное и максимальное числа не должны отличаться более чем в три раза; 2) три числа  (в наших примерах  3, 4, 5  или   5, 6, 7 )  должны быть взаимно простыми. Иначе либо будем иметь не блок, а балку, либо в будущей кладке неизбежны совпадения швов.

             Чтобы не было предвзятости, примем совершенно другую тройку чисел и попытаемся создать кладку, подобную магической (см. www.arbuz.uz/s_kladka.html )  Итак, возьмём тройку взаимно простых чисел  4, 5, 6 . Их можно применить, например, к следующим блокам двух типов:  5 x 4  и   6 x 4  . Тут всё ясно.

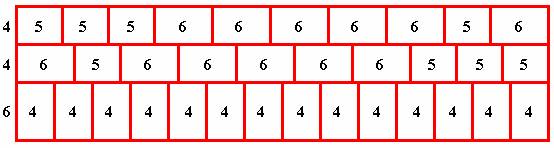
      Далее компонуем самый простой ряд, укладывая подряд  14  блоков  6 x 4 . Число  14  взято буквально «от фонаря». Мог бы принять 16  или  9 – всё равно. Чертим этот ряд в плане:

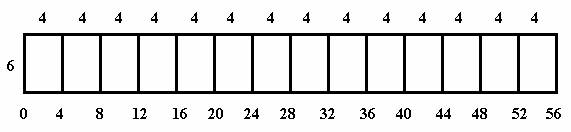
      В нижней части рисунка показаны координаты положения швов между блоками. Назовем их как «занятые»  или  «запретные». Длина секции L  получается равной  56 . Добавим еще два ряда шириной  по  4  каждый:

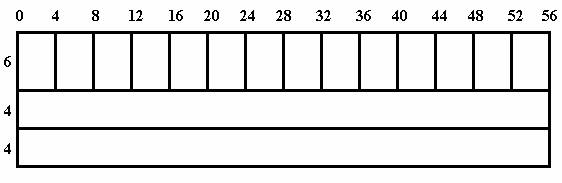
      Таким образом, имеем ширину кладки  B = 14 .  Пока неизвестно, в какой последовательности укладывать размеры  6 и 5 . Тут важно, чтобы швы нигде не совпадали. Это можно сделать при помощи комбинаторной матрицы сложения  КМС(5,6):

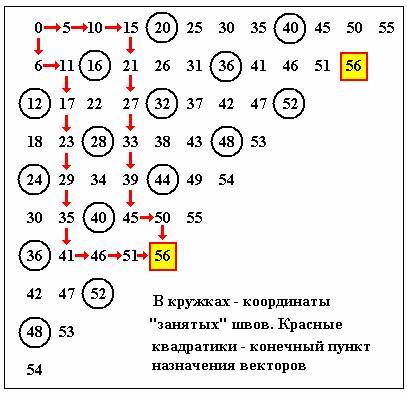
      Совершенно очевидно, что имеется единственное решение задачи, то есть по-иному невозможно вычертить два непересекающихся пути, огибающие «запретные» координаты швов. В соответствии с данной схемой продолжим начатый рисунок:

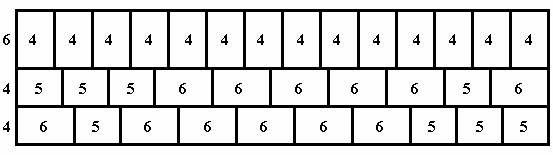
Смежный курс получается путём простой перетасовки рядов:

Если совместить оба курса кладки, то:

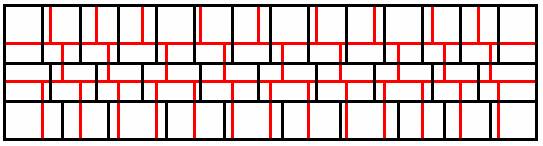
      Хорошо видно: швы ни в одном месте не совпадают.  Задача решена.

      Формула данной кладки:

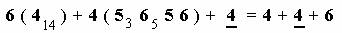
      Подчеркнутая цифра  4  -  это такой же  ряд,  как и  4  , но в нём последовательность установки блоков строго обратная.

      Лет 20 назад произошел забавный случай. Я получил похожее  решение (только исходные числа были другие) и, естественно, знал, какие габариты блоков, и какое количество их нужно было использовать, чтобы создать два курса кладки. Далее я предложил группе программистов, работавших на ЭВМ ЕС-1050, комбинаторным образом так «перелопатить» размеры двух видов блоков, чтобы найти хотя бы одно решение. (Сказав им общие плановые габариты секции и ограничения, накладываемые на соотношения размеров элементов).  Асам математики на составление программы потребовалось всего два часа, но зато и после 72 часов непрерывной работы машина не сумела перебрать все варианты и, естественно, ничего не выдала.

      Конечно же, не при всех значениях габаритов элементов получается гладко и однозначно. Бывают ситуации, когда КМС дает несколько десятков возможных ходов, а иногда решений нет и вовсе. Кроме того, существуют двухрядные компоновки, одно-двухрядные и другие. После нудной и черновой работы мною выявлены  862  структуры, пригодные для нужд строительства (это без учёта магических кладок).

      Получить хотя бы одну математическую кладку – значит охватить огромную область реальных вариантов (блоки в гидротехническом строительстве изготавливают с точностью до 1 см). Это как в пифагоровых тройках: зная числа  3 ,  4 ,  5  можно построить бесчисленное множество подобных прямоугольных треугольников, например, со сторонами  9.42 ,  12.56 ,  15.70 .

      И, напоследок, мой афоризм:

      Чтобы прослыть умным, надо не обзывать всех дураками, а показать результаты работы  своего ума

      Георгий Александров    Май 2006 г.  Москва