Комбинаторная матрица сложения

Комбинаторная матрица сложения (сокращенно КМС) – это аналог таблицы умножения и имеет общий вид:

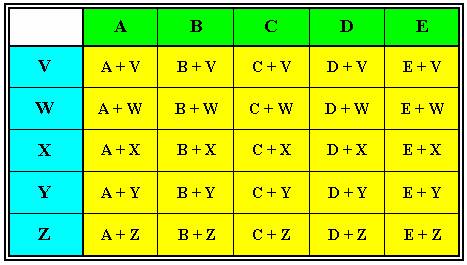
Например, если верхняя зелёная строка составлена из первых цифр числа  ПИ ,  а левый голубой столбец –  числа  Е ,  то получим следующую КМС:

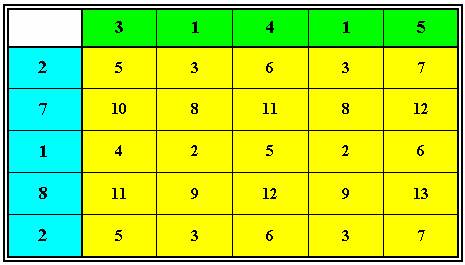
Никакой новой информации данная таблица в себе не таит. Но совсем иное дело, если в верхней строке и в левом столбце записаны числа, образующие  арифметические прогрессии. Такую Комбинаторную Матрицу сложения будем обозначать, как  КМС(u,v) ,  где u < v – постоянные исходных прогрессий. Приведем пример:

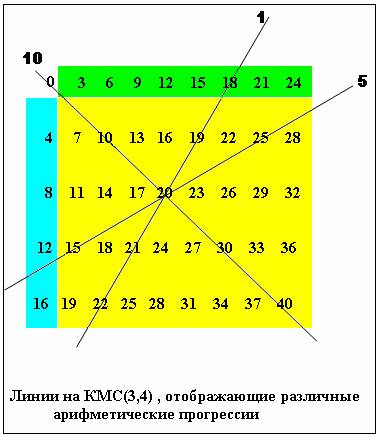
Получим линейное поле всех арифметических прогрессий. Как известно, любую прямую можно построить по двум точкам и, если на линии  КМС(u,v)  имеются три точки подряд, то между последними обязательно должны существовать определенные алгебраические связи. Найдем их. 

Проанализируем на последнем рисунке  линию  5 . Цифры, идущие подряд, такие:   15   20     25.   Как получить число  15  , если известны   числа   20  и   25  ?  Из школьной программы помним, что   15 =  20 + 20 – 25 .  Если изобразить это тождество схематично, то : 

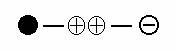
Кружочки в центре – это удвоенное число со знаками плюс,  правый кружочек - число со знаком минус, черный круг -   искомое число, равное сумме предыдущих чисел.

Точно так же находится число  25  , если известны  15  и  20 :

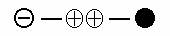
Значение   20 – это среднее арифметическое чисел  15  и  20 . Соотношение выглядит так:

Иными словами, удвоенное значение числа  20  (оно искомое) равно сумме чисел  15  и  25 .

            Данные три схемы универсальны и справедливы для любых прямых, построенных в поле комбинаторной матрицы сложения.

Очевидно, что КМС(u,v) представляет собой строгую геометрическую решётку, в которой любой элементарный четырёхугольник – параллелограмм (строки и столбцы не обязательно ортогональны). Если в поле КМС(u,v) построить любой параллелограмм, у которого все вершины совпадают с узлами матрицы, то будет наблюдаться чёткая зависимость числового значения при какой-либо одной вершине от числовых значений при оставшихся трёх вершинах. Найти алгебраическую форму такой зависимости поможет теорема.

Теорема. Если имеется произвольная плоскость, на которой вычерчен параллелограмм с координатами вершин  (X₁ Y₁ Z₁) ;  (X₂ Y₂ Z₂) ; (X₃ Y₃ Z₃) ; (X₄ Y₄ Z₄), то справедливы следующие соотношения  (индексация дана по часовой стрелке) :

X₁ = X₂ + X₄ – X₃  ;         Y₁ = Y₂ + Y₄ – Y₃  ;         Z₁ = Z₂ + Z₄ – Z₃  ;

X₂ = X₁ + X₃ – X₄  ;         Y₂ = Y₁ + Y₃ – Y₄  ;         Z₂ = Z₁ + Z₃ – Z₄  ;

X₃ = X₂ + X₄ – X₁  ;         Y₃ = Y₂ + Y₄ – Y₁  ;         Z₃ = Z₂ + Z₄ – Z₁  ;

X₄ = X₁ + X₃ – X₂  ;         Y₄ = Y₁ + Y₃ – Y₂  ;         Z₄ = Z₁ + Z₃ – Z₂  .

            Доказательство.  Докажем одно из тождеств, например,

Z₁ = Z₂ + Z₄ – Z₃ .

Пусть задана трёхмерная ортогональная система координат. На плоскости  x0y строим произвольный параллелограмм  ABCD:

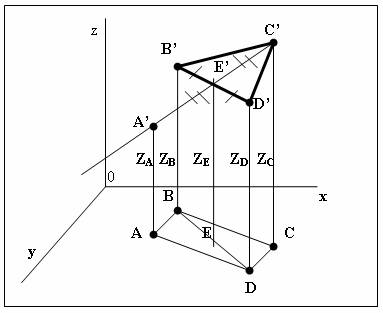
Из точек B , C , D  проводим нормали произвольной длины  Z_B ,  Z_C , Z_D . В результате будем иметь пространственный треугольник  B’C’D’.  Из точки  C’ проведём медиану  C’E’  на сторону   B’D’ .   Поскольку  B’E’ = E’D’ , то значение  Z_Е = 0,5 (Z_B + Z_D ) . Найдем разницу уровней  ∆Z точек  C’  и  E’ :

∆Z = Z_C  –  Z_E  =  Z_C  –  0,5 ( Z_B + Z_D ) .

            Продлим линию  C’E’  и отмерим на ней отрезок  E’A’ , равный отрезку  C’E’. Нетрудно убедиться, что четырехугольник  A’B’C’D’ – это параллелограмм.  Значение координаты 

Z_A = Z_Е  -  ∆Z = 0,5 ( Z_B + Z_D ) - Z_C + 0,5 ( Z_B + Z_D ) = Z_B + Z_D - Z_C .

            Что и требовалось доказать.

            Точно так же доказываются и другие тождества.         

В соответствии с данной теоремой можно находить значения чисел в вершинах любого параллелограмма, построенного на КМС(u,v).  Снова создадим КМС(3,4)  и выделим два произвольных параллелограмма, одна из вершин которых общая:

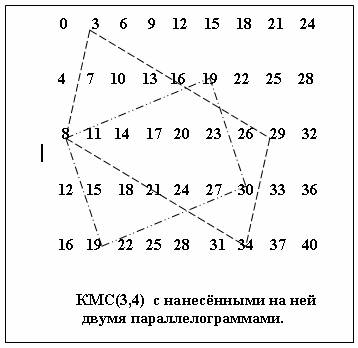
Проверим правильность значения  8  при общей вершине. Для пунктирного параллелограмма имеем :   8 = 3 + 34 – 29  ;   для штрихпунктирного параллелограмма :   8 = 19 + 19 – 30 .  Тождества выполняются.

В общем случае данное свойство можно описать следующей структурой:

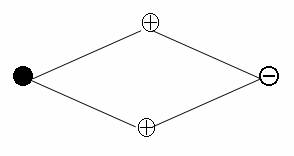
Как и ранее, черная точка характеризует искомое число КМС(u,v). Значения чисел в трёх оставшихся окружностях складываются с учётом проставленных знаков. В частности, имеем для любого прямоугольного элемента:

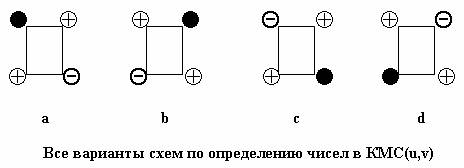
Основой любой  КМС(u,v) является элементарный треугольник. Например, из  рисунка, где показаны два параллелограмма, можно выделить элемент:

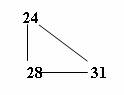
которого вполне достаточно, чтобы полностью восстановить всю матрицу от нуля до необходимых предельных границ. Если же рассмотреть элементарный параллелограмм, например,

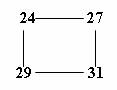
то в нём левое верхнее число, а именно  24 , является базой ячейки. Вычитая из каждого числа базу ячейки, получим:

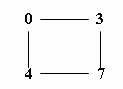
В итоге имеем самую начальную ячейку  КМС(3,4) . Рассмотрим разницы чисел по диагоналям ячейки. Они равны соответственно:  4 – 3 = 1  и  7 – 0 = 7 . Отсюда вывод: разности чисел по диагоналям любой элементарной ячейки определяются зависимостями:   v – u   и  v + u  ;    ( v > u).

            По своей сути  КМС(u,v)  -  это комбинаторная конфигурация чисел  iu + jv  ( где  i = 0, 1, 2, …  ;  j = 0, 1, 2, …) , используя которую можно  решить множество проблем. Рассмотрим простой практический пример. Имеются пять палок со следующими размерами с сантиметрах: 147 ,  182 ,  196 ,  198  и  206 . Требуется выпилить из них бруски двух типоразмеров:  25  см   и  37 см.  Целевая функция – минимум отходов.

            Для решения задачи, строим  КМС(25, 37)  и  выделяем те числа, которые максимально близки к заданным размерам, но не превосходят их:

Число брусков определяется количеством горизонтальных и вертикальных интервалов между числами. Например, из палки длиной 137 см  получаем 4 бруска длиной 25 см  и 1 брусок длиной 37 см. Все данные и вычисления при помощи  КМС(25,37)  производим  в  табличном виде:

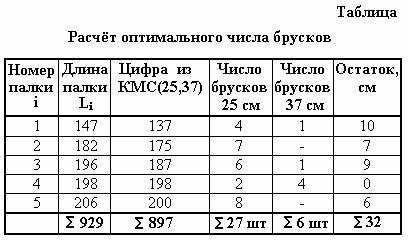
Без особых усилий выявлен оптимальный раскрой материала. Суммарный размер всех отходов - 32 сантиметра от общей длины палок 929 см, что составляет всего лишь  3,5 %. 

Комбинаторная матрица сложения является эффективным инструментом для поиска, так называемых,  простейших кладок,  но об этом – в следующей статье.

Мои новые афоризмы

Математику изучать необходимо, а развивать – престижно

Теория – это храм науки, возводимый на фундаменте теорем.

Трудно увидеть красоту в обычных вещах; ещё труднее - творить её самому.

В математике лучше не химичить.

Математика – наука более «железная», чем наши познания о железе.

Нобелевскую премию не дают ни математикам, ни дворникам.

Глубокие раздумья выше поверхностных знаний.

Трясутся малость пальцы рук, когда берутся интегралы.

Догадок блеск и красоту пора бы алгеброй проверить.

Между сложением, умножением и делением существует большая разница.

Самое прекрасное – получить невероятно красивое решение.

Великие дела не удаётся провалить за столетия.

Каждый человек – огромный мир неиспользованных возможностей.

Чтобы создать теорию, нужно иметь не только факты, но и ум, способный их увязать.

Учёный – это человек, превративший свою голову в волшебную лампу Аладдина.

Теория тогда прекрасна, когда в ней числа говорят.

Проблема, решенная при помощи математики, получает статус теории.

Минус вёл себя настолько положительно, что такое положение вещей никто не мог отрицать.

Дважды два не только четыре, но и без пяти трижды три.

Стихи чисты, как числа Фибоначчи, и дышит алгеброй поэзия Ронсара.

Из миллиона афоризмов алмазом тысяча горит.

Георгий Александров , г. Москва

27 апреля 2006 г.

Специально для www.arbuz.uz