Магическая кладка
Элементарная алгебра, и даже арифметика, способны не только быть
инструментом при вычислениях вспомогательных характеристик, но и напрямую
выдавать готовый инженерный проект.
Возьмём любые три попарно простых числа, например, 3, 4, 7. Из них
выберем крайние и создадим прямоугольник 3 * 7 . Если взять семь таких
прямоугольников, то можно скомпоновать большой прямоугольник размером 7 * 21
, как показано в верхней части рисунка 1. Это будет первым курсом кладки.
Для наглядности построения делаем на клетчатом фоне.
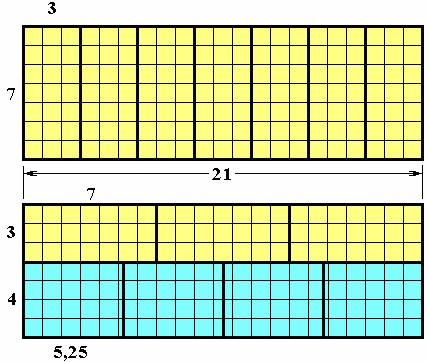
Рис. 1 Два курса кладки
Второй курс кладки создадим из двух рядов. Первый ряд выложим из тех же
прямоугольников 3 * 7, но повернутых на 90 градусов и в количестве трех
штук. Второй ряд компонуем из четырех прямоугольников 4 * 5,25 (см.
нижнюю часть рис. 1). Размеры курсов в обоих случаях одинаковы. Более того,
при наложении кладок друг на друга, нигде не совпадут швы между отдельными
элементами. Если под прямоугольниками понимать блоки-параллелепипеды, то нам
удастся создать сооружение типа опоры или фундамента. Что тут замечательно?
Оказывается, площади всех прямоугольников одинаковы. В самом деле, 3 * 7 =
4 * 5,25 = 21 . Физически же это означает, что все блоки в кладке
будут одинакового веса. Если, конечно, высота блоков принимается постоянной.
Во всем сказанном есть один недостаток – один из габаритов не является
целым числом. Чтобы этого избежать, достаточно все размеры, присутствующие на
рис. 1, умножить на 4. Если же совместить два курса один над другим (см.
рис. 2), то образуется структура, которую автор предлагает называть магической
кладкой.
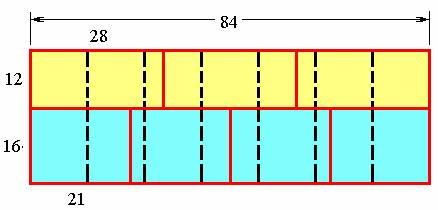
Рис. 2 Магическая кладка
Под «магичностью» понимается именно равенство площадей всех входящих в
нее элементов. Последние всегда только двух видов.
Магическую кладку легко алгоритмизировать в виде формулы кладки, похожей
на уравнение химической реакции. В нашем случае она выглядит так:
28(12)7 =
12(28)3 + 16(21)4
Левая часть равенства описывает нижний курс кладки. Число 28 перед
скобкой – это ширина ряда. В скобках дается второй габарит прямоугольника -
число 12 . Индекс 7 указывает на количество таких
прямоугольников в ряду.
Правая часть уравнения – вышележащий курс. Два слагаемых - это два ряда.
Сначала устанавливается ряд шириной 12, состоящий из трех прямоугольников
длиной 28 каждый. К нему примыкает ряд шириной 16, состоящий из
четырех прямоугольников длиной 21 каждый.
Благодаря четкости и компактности формулы кладки, имеется возможность
производить построения структур с помощью компьютера.
Мы рассмотрели случай, когда в магической кладке применяются не более
двух рядов в курсе. Есть примеры и более широких кладок. Построим структуру, в
каждом курсе которой имеются по три ряда. Так, при выборе попарно простых
чисел: 3 , 4 , 5 , - можно получить кладку, изображенную на рис. 3:
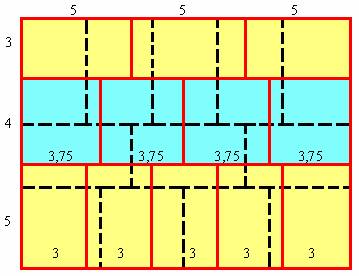
Рис. 3 Трехрядная кладка
Ширина структуры 12, её длина 15. Здесь также 5 *
3 = 4 * 3,75 . Избавимся от дробного габарита 3,75 путем
умножения всех чисел на четыре. Окончательная компоновка показана на рис. 4:
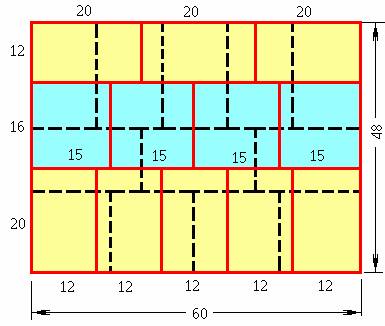
Рис. 4. Целочисленное представление
Формула
этой магической кладки будет такой:
20(12)5 +
12(20)3 + 16(15)4 = 12 + 16 + 20
Заметим, что в правой части уравнения для краткости пишутся только ширины
рядов.
Подобных компоновок можно найти бесконечное количество, но лишь десятки
из них приемлемы для создания реальных сооружений. Таких как опоры мостов,
колонны, постаменты и т.д.
В любой методологии, как правило, выявляется критерий, увязывающий
множество параметров задачи. В нашем случае в качестве такого критерия может
стать связь между реальными характеристиками кладки и ее математической
моделью. Реальные характеристики – это масса блока, связанная с
грузоподъемностью кранового оборудования M ,
длина кладки Lo и ее ширина Bo , высота блоков h ,
плотность материала ro , из которого блоки
сделаны. Размер швов между элементами пока учитывать не будем. Параметры
магической кладки: длина L, ширина B, габариты любого из двух прямоугольников l * b
. Последние четыре характеристики выражены целыми числами.
Приступаем к анализу. Предположим, что главным расчетным элементом кладки
является ее ширина. Тогда можно выразить линейный коэффициент масштаба k :
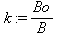
В соответствии с законом моделирования, реальные
размеры габаритов блока равны:
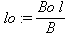
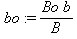
При соответствии массы блока грузоподъемности крана справедливо соотношение:
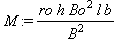
Если же разделить математические и физические параметры, то будем
иметь красивую связь:
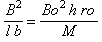
Так
вот откуда появляется критерий, когда делалась студенческая работа по
проектированию вертолётной площадки! Не один я такой умный, однако!
Ничто нам не мешает принять в качестве основного критерия кладки K правую часть последней зависимости
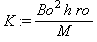
Задача
теперь сводится к тому, чтобы найти такую магическую кладку, у
которой 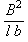 равнялась бы K. равнялась бы K.
Для
первой рассмотренной нами структуры:
282/(28·12) = 7/3 = 2,333333…
Для трехрядной магической кладки:
482/(20·12) =9,6
Если
допустимые параметры M , Bo, h
и ro таковы,
что критерий K равен
либо 2,3333 , либо 9,6 , то одна из выявленных нами магических
кладок может быть с успехом применена на практике. Имея же обширный банк
математических структур, наверняка удастся найти самую выгодную.
Чтобы легче было запомнить формулу для вычисления значения K,
автор придумал незатейливый стишок:
Квадрат опоры ширины
На блока высоту умножим.
На плотность среднюю стены
Сомножители множим тоже.
Все это, достигая цели,
На силу крановую делим.
Вот так на листике тетрадки
Находится критерий кладки.
Георгий Александров
20 апреля 2006 г Специально для www.arbuz.uz
| 
