Веселые фракталы

Опубликовано в Компьютерре от 30 августа 2005 года

— Какие чудные цветы! — воскликнула Элли.
— Они хороши! — молвил Страшила.
— Конечно, будь у меня мозги, я восхищался
бы цветами больше, чем теперь.
А. Волков. Волшебник Изумрудного города

Если начать словами, что фрактальные изображения обладают психоэмоциональным воздействием, ибо несут в себе субъективную эстетическую составляющую… то есть риск навечно получить клеймо непроходимого зануды. Потому что заумные казенные фразы менее всего сочетаются со сказочными картинками, проступающими вдруг на мониторе. Больше всего напрашивается анекдот: «Звонок в магазин тканей – У вас есть что-нибудь с веселой расцветкой? – О, да, приезжайте, есть такой ситчик – обхохочитесь!»

Просто рассмотрите картинки и подумайте о том, что это всего лишь комплексные числа, возводимые многократно в степень! А возможность увидеть эти россыпи веселых огоньков дает незамысловатый прием. В отличие от множеств Мандельброта и Жюлиа, получаемых возведением комплексного числа в квадрат, мы применяем формулу Муавра для возведения комплексных чисел в степень. Это позволяет расширить рамки опытов, возводить комплексные числа в произвольную степень, в том числе дробную и отрицательную.

И происходит чудо – картинки, также как и с положительными показателями степени имеют форму с количеством лепестков-отростков, равным показателю степени, но вместо привычных лохмато-колючих фрактальных зарослей появляются вдруг цветочки-фонарики-бабочки с гладкими краями. При попытке задать отрицательное дробное значение количество лепестков также становится не целым, переходя, вслед за показателем степени от одного целого значения к другому. Тот, кто развлекался с фигурами Лиссажу или розетками (эпи- и гипоциклоидами) в полярных координатах, заметят аналогию – при увеличении множителя угла картинка становится острой и лохматой, а при уменьшении до дробных долей – плавной и округлой.

Рассмотрим еще две картинки, отличающиеся только знаком показателя степени. (Это работа Java-аплета, разработанного моей знакомой - поиграйте с ним при случае – у каждого есть возможность создать новый фрактал.)

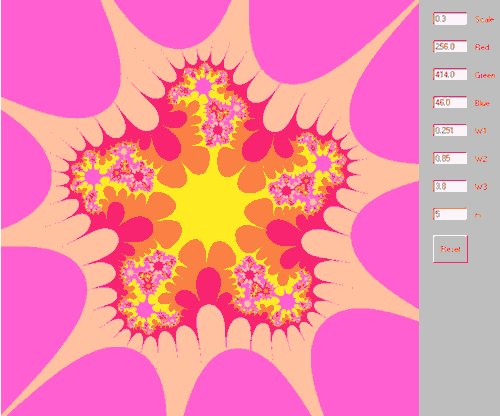
Сравнивая их мы увидим работу самого загадочного математического преобразования – инверсии. То, что было периферией, становится центром, а центр – периферией, рисунок как бы выворачивается наизнанку, страшные колючки и шипы превращаются в цветочки и мотыльков. Была такая математическая шуточная задача: «В клетке сидит лев, рядом с клеткой стоит дрессировщик, происходит инверсия, когда лев окажется снаружи, а дрессировщик внутри клетки?»

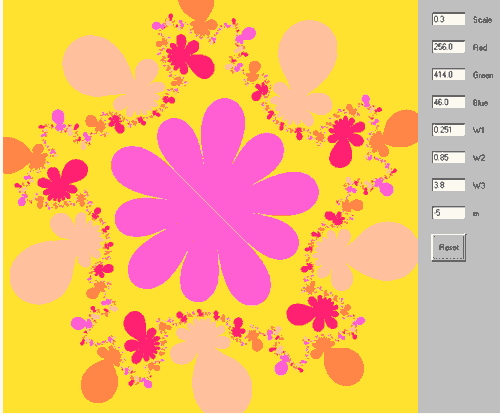
Самое главное, что здесь присутствует эстетический и даже эмоциональный момент. Напоминает методику холодинамики лечения заболеваний, связанных с психическими травмами методом вызова ассоциаций и работы с ними. Исчезновение колючек у картинки-асоциации влечет за собой освобождение от недуга, чего всем и пожелаем. Инструкция излечения проста: подобрав комфортный для вас цвет задаете положительный показатель степени, разглядывая полученный фрактал мысленно связываете каждую колючку с травмами и обидами из своего детства и даже более ранними (вспоминать все не нужно, достаточно формально связать), задаете отрицательный показатель (такой же по значению обязательно!) и рассматриваете полученный рисунок. Статистика излечившихся свидетельствует о действенности метода. Так что комплексные числа не просто красивые, но веселые и целительные, надо только вызвать их на экран, приобщайтесь.

Примечание. Надеюсь, на последней картинке видны вводимые параметры - начните с них. На стареньких слабых компьютерах апплет работает несколько минут, на последних моделях несколько секунд - дождаться стоит!

Пояснения к параметрам:
scale - масштаб картинки
Red, Green, Blue - коэффициенты, влияющие на раскраску фрактала
W1, W2 - возмущения при возведении в степень для реальной и мнимой составляющих соответственно
W3 - определяет условие выхода их цикла - чем больше, тем больше шагов.
m - показатель степени, в которую возводится комплексное число, самые интересные целые значения от ±3 до ±12