Уравнение Эйлера

История математики оставила нам поразительно красивые проблемы, среди которых есть и нерешенные до сих пор. Об одной из задач, известной как задача о четырех кубах, пойдет речь в данной статье. Почему-то именно диофантову формулу, предложенную впервые Эйлером, крайне скудно освещают современные популярные труды. Отрывочные сведения удалось найти лишь в Интернете, в работе Г.Харди «Двенадцать лекций о Рамануджане» и справочных пособиях по математике.

Леонард Эйлер (1707—1783 гг.) - математик, механик, физик и астроном, ученый необычайной широты интересов, автор свыше 800 работ по математическому анализу, дифференциальной геометрии, теории чисел, приближенным вычислениям, небесной механике, математической физике, оптике, баллистике, кораблестроению, теории музыки и др., оказавших значительное влияние на развитие науки. По происхождению швейцарец.

В 1726 г. был приглашен работать в Петербург, в 1727 г. переехал жить в Россию, в 1731—1741 и начиная с 1766 гг. был академиком Петербургской академии наук. В 1741—1766 гг. работал в Берлине, оставаясь почетным членом Петербургской Академии наук.  

Математика, вне всякого сомнения, была и будет самой удивительной наукой, рожденной в головах многих выдающихся личностей. Она возникла и совершенствовалась в соответствии с нуждами практики, но оказалась настолько цельной и гармоничной, что сама явилась объектом тщательных исследований. Величайшие умы человечества, иногда по крупицам, а иногда и гейзером идей, открывали все новые и новые грани теории чисел, статистического анализа, изучения функций, дифференциального и интегрального исчислений, рядов, геометрии, тригонометрии, графов, топологии и т.д. и т.п. Основной целью математики чаще всего было нахождение области допустимых решений нужной задачи. Когда та или иная сложная проблема вдруг стопорилась, приходилось искать иные подходы, методы и даже создавать новые направления, которые позволяли преодолевать пробелы в математических знаниях. Так происходил прогресс науки о порядке.. Наиболее ярким примером сказанному служит, конечно же, Великая Теорема Ферма. Потребовалось целых 358 лет, чтобы ее безошибочно  доказать!

В уравнении  Эйлера

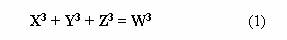
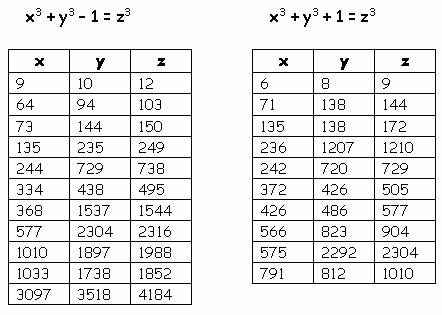
значения  X , Y , Z  и   W   целочисленные. Данная математическая головоломка известна еще как задача о четырех кубах. Требуется найти все ее решения.  Отдельные арифметические результаты были известны еще Диофанту – древнегреческому математику, занимавшемуся вопросами анализа уравнений с целыми коэффициентами. Сколь угодно большое количество четверок чисел можно найти при помощи элементарной программы на компьютере. Вот некоторые варианты:

Но общей формулы, позволяющей находить данные значения, выявить до сих пор не удалось.

Суммируем  все,  что  известно

Вот два варианта, найденные великим индийским математиком Рамануджаном  (1887 – 1920 гг.):

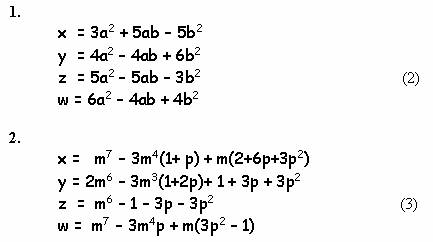
В 1956 году  математик  Л. Мордел (см.ссылку   http://neves.suncloud.ru/task/fermat25.htm) получил следующие весьма любопытные  двухпараметрические зависимости:

Выведенное мною объединение последних вариантов (4) и (5)  дает еще одно решение:

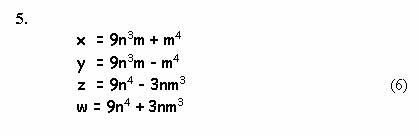
Математиками давно было доказано, что любое рациональное число можно представить в виде суммы трёх кубов рациональных чисел. Наглядно это демонстрирует потрясающая по красоте формула, полученная еще в 1825 году:

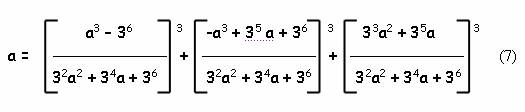
            где  а – любое действительное число. Отталкиваясь от данного соотношения, мне довольно легко удалось найти громоздкое однопараметрическое решение уравнения  Эйлера:

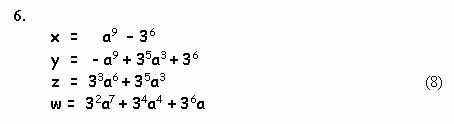
Вычислим для интереса несколько значений коэффициентов уравнения :   

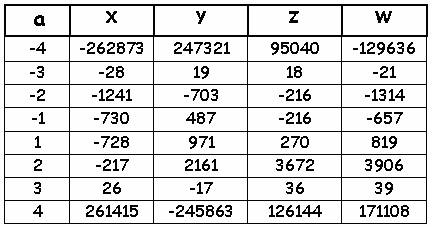
И 1955 году математик Д.Лемер  обнаружил еще один необычный вариант:

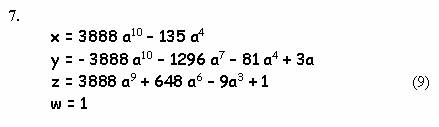
Простейшие численные решения такие:

Ссылка  http://rusnauka.narod.ru/lib/matem/labkovsky/ привела меня к интересной работе  «Элементарные уравнения Диофанта», написанной преподавателем математики Лабковским Виленом Борисовичем.  В ней приведено довольно простое решение уравнения (1):

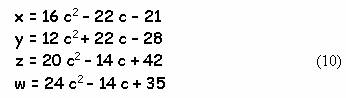
Совокупность (10) , как ни странно, допускает существенное упрощение.  В самом деле, если произвести замену     а = 0,5 c  ,  то :

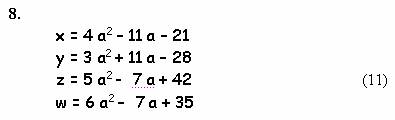
               Мы кратко обрисовали состояние дел по интересующему нас вопросу.  Можно было бы попытаться  найти еще больше формул, но, как мне кажется, и восьми примеров вполне достаточно,  чтобы показать всю сложность проблемы. Складывается такое ощущение, будто представленные алгебраические связи выведены простым интуитивным подбором. Часть решений получаются при изменении одного параметра (примеры  №№ 6 – 8), а часть – при изменении двух параметров (примеры №№ 1 – 5).

Исследования автора

Моя цель – дать наиболее общие связи для четырёх параметров в уравнении Эйлера, из которых, как частные случаи, могли бы отпочковываться четверки целых чисел.

Методом проб и ошибок, анализом огромного количества конкретных вычислений и вовлечением в этот процесс таинственной интуиции, мне удалось сформировать до сих пор непонятные, но чудотворные соотношения: 

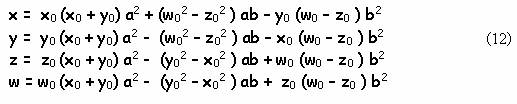
Если в (12) подставлять в качестве начальные значений параметров любые известные целые числа, удовлетворяющие уравнению (1), то, как из рога изобилия, будут находиться  другие решения. Подтвердим сказанное на нескольких примерах. Примем в качестве начальных параметров такие:

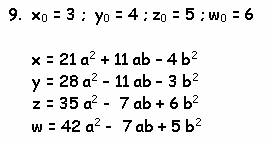
Параметры можно перетасовывать, получая новые связи:

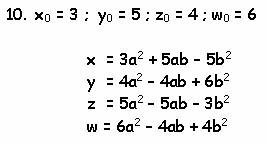
А это как раз и есть система  (2), полученная Рамануджаном! Просто потрясающее открытие! Знал ли великий индийский математик о существовании решения (12) ?

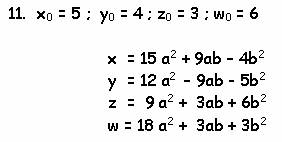
Подобные формулы можно без особых усилий составить из других вариантов чисел   x₀ ;  y₀ ; z₀ ; w₀ .  Каждая такая система, тем не менее, -  на вес золота, поскольку открывает новое поле конкретных решений.

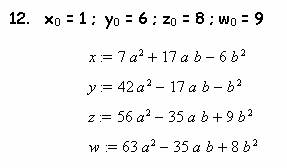
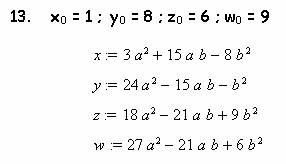
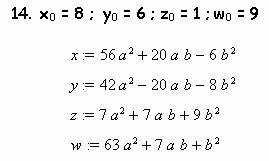
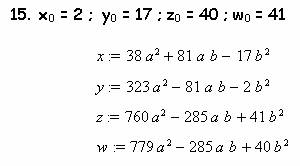
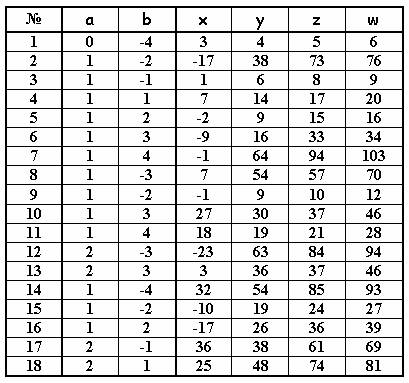
Подставляя эти данные опять в ту же программу, выявил еще  47  вариантов

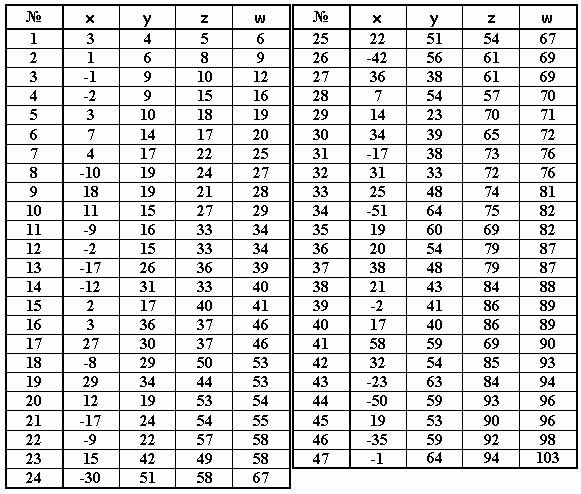
К сожалению, никак не проявили себя следующие 20 четверок чисел:

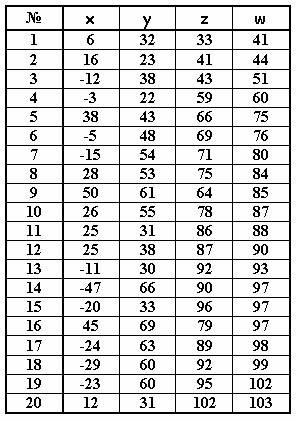
Как получить эти последние решения – совершенно неясно. Утешением может служить только то, что приблизительно 74%  вариантов найдено по цепочке с помощью системы (12)  опираясь только на  начальные  параметры  x₀ = 3 ;  y₀ = 4 ;  z₀ = 5 ;  w₀ = 6 .  А это совсем немало.

Георгий Александров

26 мая 2006 г.

Специально для www.arbuz.uz