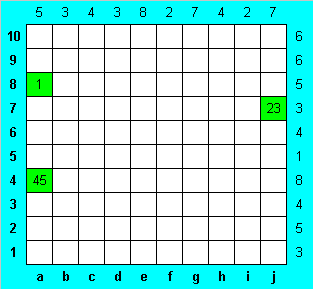
На рисунке изображено условие задачи.
Для удобства занумеруем строки снизу вверх числами от 1 до 10, а столбцы - слева направо латинскими буквами от a до j. Будем рисовать зеленым (змеиным) цветом те клетки, про которые точно известно, что они - часть змеи. Клетки, где змея быть не может, отрисуем серым. Действия, совершенные на данном шаге решения, изобразим более ярко, чем старую информацию.
Сразу изобразим голову, хвост и середину - части змеи.
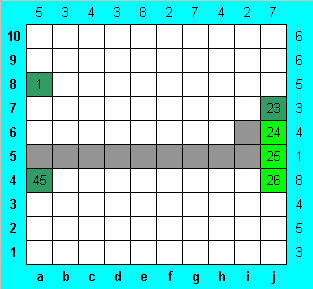
Для краткости любую строку или столбец будем называть рядом.
Если в одном из рядов стоит 1, то змея проходит через него лишь один раз, и делится на две части: до этого ряда и после. Если в ряду, не содержащем концов змеи, стоит 2, то возможны два варианта: если концы по разные стороны от ряда, то змея проходит по этому ряду один раз по паре соседних клеток. А если концы змеи лежат по одну сторону от этого ряда, то змея проходит через ряд дважды по одной клетке. Именно поэтому в столбце j все семь клеток заняты одним блоком змеи - змея только единожды заходит и выходит из него. Представив самое верхнее и самое нижнее возможное расположение этого блока, убеждаемся, что несколько клеток (j4-j7) он покрывает в любом случае. И сразу же в пятой строке отмечаем серым цветом все оставшиеся клетки.
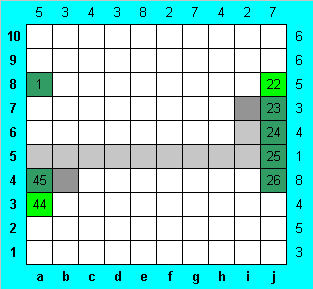
Большинство столбцов оказались разбитыми на две части. В столбце "a" в верхней части заняты змеей не более, чем три клетки (если из 1-й своей клетки змея идет вверх, то пусты две a6 и a7, а если вниз - то пусты a9 и a10). Поэтому в нижней части столбца находятся по крайней мере две клетки змеи. Мы убедились, что соседняя с концом клетка (a3) также принадлежит змее (отмечаем ее числом 44).
Допустим, что змея имеет излом в своей середине. Тогда она в 7-й строке имеет три клетки единым блоком (так как поворачивать в столбце "i" не может), и не может иметь никаких других клеток в 6-й строке, что противоречит условию. Следовательно, блок длины 7 в столбце "j" занимает не самое нижнее положение. Это дает нам возможность отметить клетку j8 числом 22.
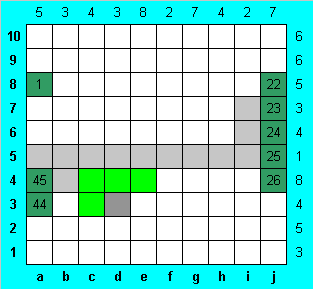
В четвертой строке не заняты змеей лишь две клетки, причем одна из них известна. Допустим, что свободна также клетка c4, то есть в строке имеется цельный блок длины 7 от d4 до j4. В этом случае в третьей строке все шесть правых клеток пусты, поэтому должны быть заполнены четыре левых, то есть змея не доходит до нижних строк. Противоречие. Поэтому клетка c4 - часть змеи. Поскольку пара ее соседей пусты, змея может продолжаться от нее лишь в паре других клеток - d4 и c3. Наконец, можно заполнить еще и e4, поскольку змея не может касаться себя в клетке d3.
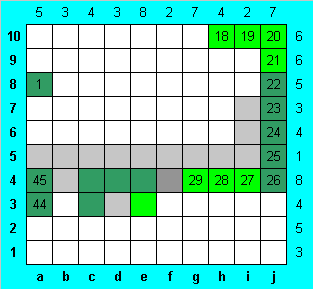
Может ли быть заполненной клетка f4? Допустим, что это так. Тогда получается, что остальные клетки в нижней части столбца "f" должны быть пустыми (вторая клетка из двух обязательно занята верхней частью), а в соседнем столбце "e" клетка e3 пуста, поэтому заполнены две нижние клетки e1 и e2. Змея в тупике - она не может продолжиться, не коснувшись себя. Опять противоречие. Поэтому клетка f4 пуста, а змея после e4 заворачивает на e3. Далее заполняем змеей все оставшиеся клетки четвертой строки.
Основной рывок в решении сделан, далее решение льется, как по маслу, его можно продолжать многими способами. Отметим, что в самом правом столбце семиклеточный блок занимает наивысшее положение.
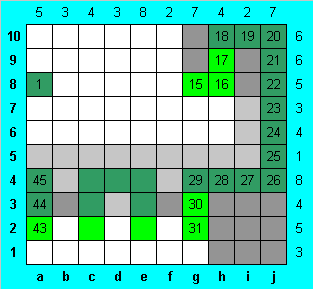
Продолжаем поворот змеи в третьей строке и столбце "g", отмечаем пустые клетки в столбцах "i" и "j", убеждаемся, что оставшиеся две клетки в столбце h могут быть заполнены единственным образом. Далее, замечаем, что в третьей строке все четыре клетки уже заполнены, и змея может продолжаться лишь вниз - на клетки g2, e2, c2 и a2.
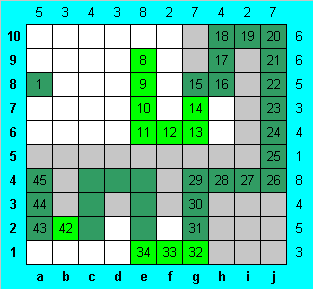
В столбце "g" заполняем все клетки, кроме трех пустых, и единственным возможным образом продолжаем змею. В первую строку змея входит лишь один раз, поэтому мы можем единственным образом замкнуть части змеи во второй строке.
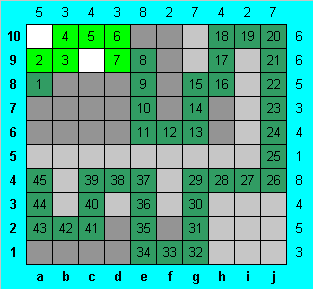
Пользуясь цифрами на границах, отмечаем все очевидно пустые клетки (уже больше ради эстетики, чем по необходимости). Осталось вырисовать начало змеи в левом верхнем углу. Единственным возможным образом (мы двигаемся от хвоста к голове) в 9-й строке переходим из столбца "e" в столбец "f", за счет тройки в этом столбце поднимаемся вверх, пройдя три клетки, снова спускаемся вниз, и чтобы было соответствие между змеей и определяющими ее цифрами, завершаем движение в столбце "a". Все, задача решена.