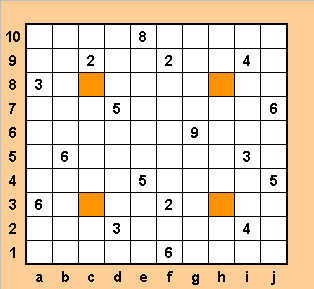
Как обычно, обозначим строки цифрами, а столбцы - буквами. Отметим, что в задаче количество пустых клеток должно быть равно сумме всех расставленных на поле чисел. Ключевых вопросов, помогающих восстановить картину, обычно бывает два:
А. Откуда может прийти отрезок в эту клетку?
Б. Куда от данного числа точно выходит отрезок?

Умение решать сводится, в основном, к тому, чтобы в нужном месте (на нужных клетках и для нужных чисел) задавать эти вопросы и находить ответы на них. Именно так и будем строить решение: указываем клетку и вопрос, который задаем, а также ответ на этот вопрос.

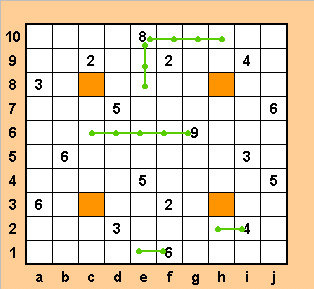
Будем также по ходу выделять те клетки с цифрами, все отрезки из которых уже проведены. Итак, начали...

Клетка f1, вопрос Б. Сумма отрезков,выходящих вверх и вправо от этой клетки, не более пяти, значит, есть отрезок, идущий влево. Отмечаем его.
Клетка с6, вопрос А. Убеждаемся, что идти в эту клетку отрезок может лишь от g6.
Клетка h2, вопрос А. Отрезок может идти лишь из i2. В клетку h10, как и в клетку е8, линия может идти лишь из е10.

Обратите внимание, что здесь уже существенно используется ранее полученная нами информация: если бы не линия из девятки на g6, то отрезок мог бы достигать клетки е8 и из пятерки на е4.

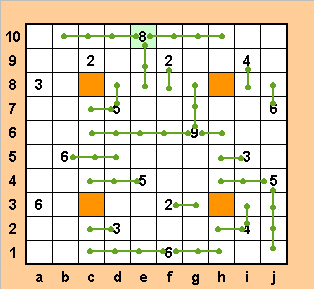
Далее в течение некоторого числа шагов мы будем лишь указывать номер клетки, отрезок до которой вычисляются однозначным образом, и рисовать отрезки (следите по рисунку): c7, с5, с4, d5, с1, с2, d8, f8, g8, j8, h6, h5, h4, j3, j1, h1, i3, g3, i8, b10. Все отрезки из восьмерки на е10 проведены, отмечаем эту клетку.

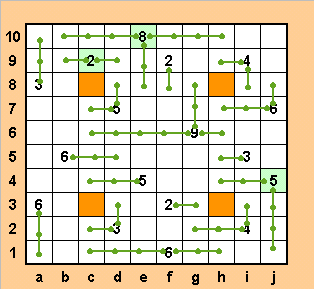
Продолжаем: а10, а1, d3, h9, h7, g2. Замечаем, что из двойки на с9 можно провести лишь два отрезка длины 1, проводим их, выделяем клетку с9, также как и давно ожидающую этого клетку j4.

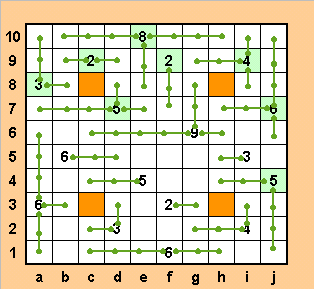
Можно для разнообразия сделать несколько шагов, задавая вопрос Б. Убеждаемся, что из шестерки на а3 неизбежно идет отрезок длины хотя бы 3 вверх, а из шестерки на j7 можно продолжить отрезки вниз и вверх. Из пятерки на d7 удлиняется отрезок влево и проводится отрезок вправо. Из четверки на i9 отрезки провести можно лишь однозначным образом. Воспользовавшись этим, проводим однозначно отрезок вниз из двойки на f9. И пятерке на d7 стало тесно, она продолжает свой отрезок до а7, "уплотняя" тройку на а8, которая теперь вынуждена "пустить корень" вправо на b8. Да и шестерка на а3 вынуждена "пустить корень" вправо. Клетка j10 может быть заполнена лишь из шестерки на j7.

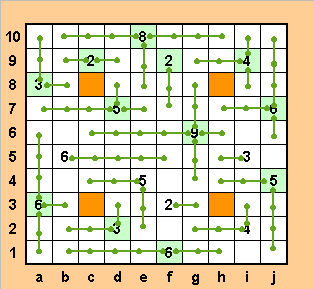
Развязка близка: верхняя часть доведена до ума. Продолжаем до конца: из шестерки на b5 удлиняем на 2 отрезок влево, заполняем клетку b2 единственно возможным способом, от тройки на d2, а клетку b1 - от шестерки на f1. Выделяем клетки с этими числами. Клетка е2 может быть заполнена только от пятерки на е4, и клетка g4 достается только из девятки на g6. Этот рывок, по сути, и был заключительным в решении, девятка оказалась полностью использованной, и осталось лишь навести заключительные однозначные штрихи.

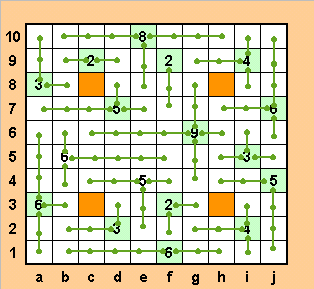
Проводим вправо и вверх отрезки из тройки на i5, вниз - из четверки на i4. В клетку f2 из двойки на f3, в клетку f 4 - из пятерки на е4. Заполняем оставшиеся свободными клетки b4 и b6 из шестерки на b5. Убеждаемся, что задача решена верно.

Несмотря на красоту и увлекательность процесса решения головоломок этого типа, описание (и, возможно, также чтение описания) этого самого процесса оказалось делом весьма занудным. Так что лучше, может быть, постигать тонкости процесса на практике - не вникая в занудные записи ;-).